矩阵相似性分析
0、简介
|
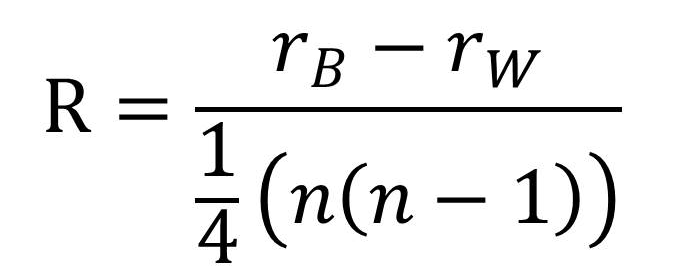
1
2
3
4
5
|
data(dune)<br>data(dune.env)dune.dist <- vegdist(dune)dune.ano <- with(dune.env, anosim(dune.dist, Management))summary(dune.ano)plot(dune.ano) |
summary(dune.ano)结果为：
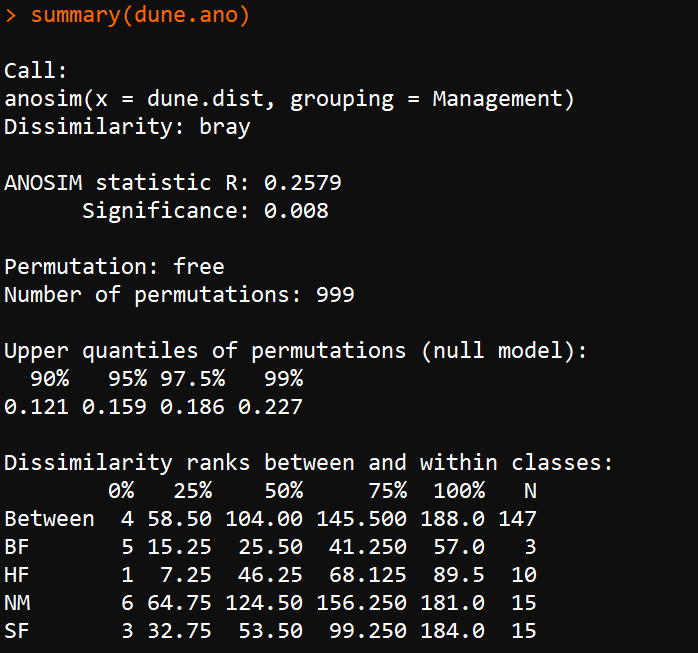
plot画出的图形为：
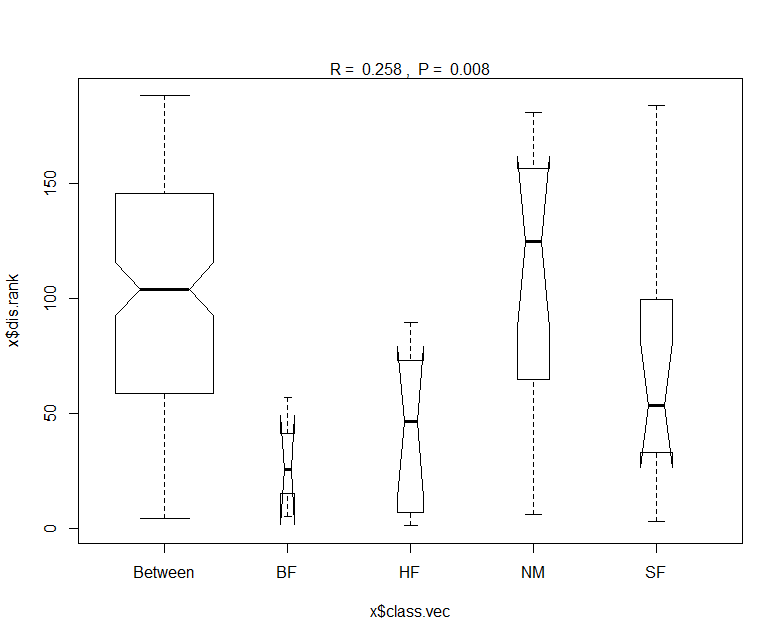
不难看出，图中箱子为summary结果中的Dissimilarity ranks between and within classes的可视化，即组间差异秩分布和组内差异秩分布（下图中的数值分布）。
一、beta多样性简介
Beta多样性作为群落结构研究的根基， 常用来比较不同生态系统之间的差异，反映生物种类因环境所造成异质性。通俗来讲，不同的处理（环境、健康状态等），会导致群落结构产生变化。往小了说，也就是物种分布情况的改变，一般通过指示物种分析，定位具体的差异物种，就能阐明驱动群落变化的主要物种因素；往大了说，还可以研究处理效应对样本乃至分组的影响，这个时候Beta多样性就发挥了其作用！
指示Beta的方法有很多，在文章中常见的有-距离指数（Jaccard、Bray-Curtis、Unifrac）；排序分析（PCA、PCoA、NMDS）；聚类分析（UPGMA）；差异分析（adonis、anosim）等几大类。通过这些分析如PCA、PCoA等，能在实验前期帮助规避很多风险，例如，揭示分组是否符合预期，采样是否合理，还可对离群样本进行剔除等。
无论聚类还是排序分析，从分枝或散点距离，例如图1[1]，能明显看出三个分组有差异，这种通过人眼的差异结果带有强烈的主观性，缺乏证据，也就是常说的统计学数据，会受到学术质疑。
因此今天给大家介绍两种组间差异的检验方法--ANOSIM、ADONIS。相较于普通的统计检验，像两组比较的Wilcoxon秩和检验、多组kw秩和检验等等。ANOSIM、ADONIS不但能输出显著性p值，来判定比较组之间是否存在差异，还可以额外给出差异的程度（R值），来揭示不同因素对群落变异的贡献。废话不多说进入正题！
ANOSIM、 ADONIS都是基于相似性（距离矩阵）的非参数检验，由于不要求数据正态分布和方差齐性，非常适用于微生物群落这种样本分布不确定的复杂分析。在β多样性中常被看作一个量化的数值，来反应每个组内各个样本间的群落物种组成差异。接下来带大家感受ANOSIM、PERMANOVA原理的奇妙之处。
二、ANOSIM原理简介
ANOSIM[2]（Analysis of similarities）是在1993为解决多物种丰度数据的普遍适用性，而开发的非参检验，至今已被引用14285次，在群落多样性研究中极具权威性。
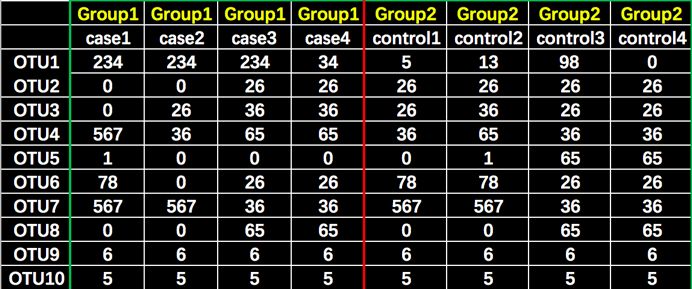
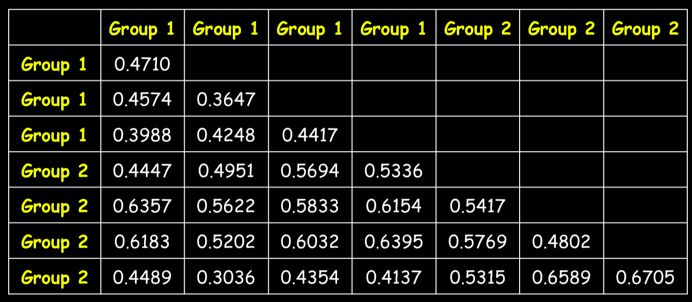
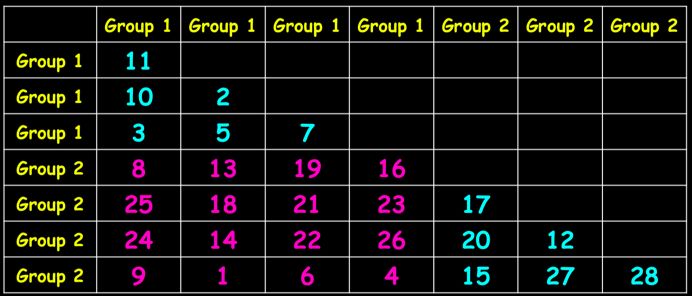
首先，通过变量（物种/OTU等丰度信息）进行样本关系计算，得到距离矩阵（图2 a），距离类型可以是常见的Bray-Curtis，同样Jaccard、Unifrac也适用；
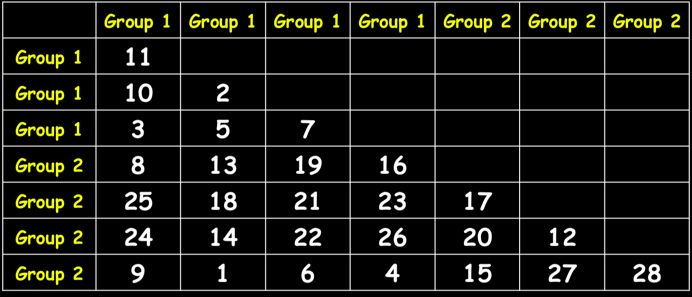
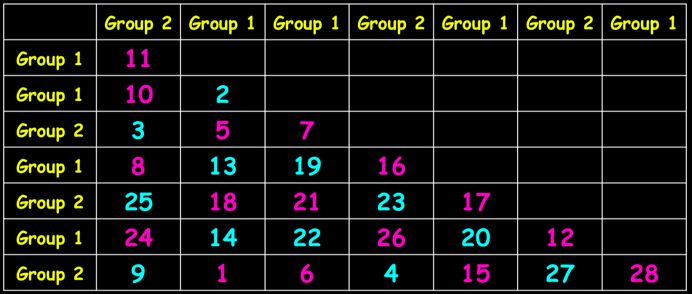
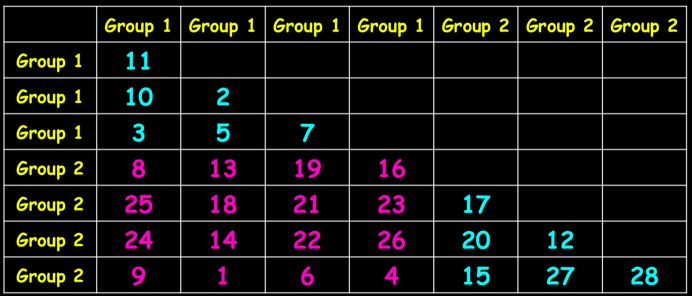
接着，对样本关系从小到大进行排序，最小的距离记为1，依次类推为2，3，4……得到排序后的关系排名（秩）（图2 b）；
然后，用上述的秩计算R；
其中：
rB=组间秩的平均值（排序后组间距离的平均值），即图2 b中，橙色区域的平均值，rB=（13+14.5+14.5+7+9+2+4+6+5）/9=8.33；
rW=组内秩的平均值（排序后组内距离的平均值）；即图2 b中，蓝色区域的平均值，rW=（3+10+8+1+12+11）/6=7.5；
n为总样本个数。
最后，通过置换检验求p，将样本打乱随机分组，计算置换后的R值（记为Ri），经过N次置换后（至少1000次），Ri大于原始R的概率即为p。
ANOSIM结果输出解读（表1）：
其中：
Diffs：差异比较组；
R：差异程度，一般介于（0，1）之间。
R>0，说明组间存在差异（R>0.75：大差异；R>0.5：中等差异，R>0.25：小差异）；
R=0或在0附近，表明组间没有差异；
若R出现<0的情况，说明组内差异显著大于组间差异，这个时候表明分组或采样不合理，需要重做实验。
Pvalue：P值，数值小于0.05、0.01或在两者范围内，表明分组有显著性差异，进而反映出目标分组有意义。
三、Adonis原理简介
Adonis[3]（non-parametric multivariate analysis of variance），是在ANOSIM 和MANOVA 基础上于2001年开发的另一种分组差异检验方法，在文献中可能大家比较熟悉的是PERMANOVA这个别称。其作用与ANOSIM类似，通过统计检验的p值来判断分群效果是否显著，再辅佐R值判别差异程度！
但两者也有所不同，Adonis的检验模型更多的是借鉴了MANOVA（多元方差分析），本质是基于F统计量的方差分析，利用各种组间距离指数对总方差进行分解，可以分析不同分类因子对群落差异的解释度，并使用置换检验进行统计学检验。
检验原理第一步与ANOSIM一致，计算样本间的距离矩阵，但不再对距离矩阵进行排序；
然后，依据距离矩阵计算F值；
其中：
SST=所有分析对象的平均距离；
SSW=组内平均距离（SSW）；
那么组间平均距离为SSA= SST– SSW；
N为总观测数，a为组数。
最后，同样通过随机置换的方式得到p值，先计算多次置换后的伪Fi值（p值精度会随着置换次数的增加而增加，一般来说，精度为0.05至少1000次，精度为0.01至少5000次），当伪Fi值大于原始F观测值的概率即为p值。
以上就是Adonis的原理部分，接下来带大家解读输出的Adonis结果表中（表2），各部分内容所代表的含义。
其中：
Diffs：差异比较组；
Df：自由度；
SumsOfSqs：总方差，又称离差平方和；
MeanSqs ：均方（差），即Sums Of Sqs/Df；
Fvalue：F 检验值；
R2：不同分组对样品差异的解释度，即分组方差与总方差的比值，
R2 越大表示分组对差异的解释度越高；
Pvalue：P值，值越小可信度越高。
四、案例应用
Adonis和Anosim在文章中展示的方式有多种，下面就通过几篇应用案例，解锁Adonis和Anosim在高分文献中的花式用法。
案例一：表格展示法[4]
发表期刊：Nature Microbiology（Nature子刊）
影响因子：17.745
发表时间：2021年12月
作者在前期α多样性分析中，得出人体测量指标（治疗和安慰组）之间并没有显著差异，因此继续探索肠道菌群在3个不同年龄组（7-12个月、1-2岁和2岁以上）的beta多样性，以期揭示非洲农村婴儿的肠道菌群受年龄影响的变化规律（表3）。
结果显示年龄组间的PERMANOVA检验和相似性ANOSIM分析的P值为0.0003，表明beta多样性在不同年龄组之间具有显著性差异。
Tips
上述这种直接用表格展示Adonis和Anosim检验结果的方式，仅建议在文章内容极其丰富的情况下，一般推荐用下面这两种方式进行可视化呈现。
案例二：与PCOA、NMDS等搭配法[5]
发表期刊：Genome Medicine
影响因子：11.117
发表时间：2021年9月
作者通过对表现为MCII（minimum clinically important improvement）的患者（MCII+）和没有表现出MCII的患者（MCII-）的多样性研究，探索类风湿关节炎（RA）患者特征的肠道微生物群落差异（图3）。
PERMANOVA结果表明，MCII患者组肠道微生物群落之间具有显著性差异（p=0.002），并且对群落总变异的贡献为3.8% (R2=0.038)。
案例三：盒型图展示法[6]
盒型图是统计检验的经典展示图，例如在下面这篇案例中 。
发表期刊：BioMed Research Internationa
影响因子：2.0
发表时间：2020年6月
作者旨在探讨血液透析对尿毒症患者微生物群落的影响，将患者分为血液透析组（A组）、血液透析+血液透析滤过组（B组）、血液透析+血液透析滤过+血液灌注组（C组）、成人终末期肾脏病ESRD患者（CK组）进行多样性分析（图4）。
Anosim结果表明，CK组与透析组的菌落分布有显著差异；三种不同透析方式患者的菌落分布也有显著差异。
总结：
1）在文章中Adonis和Anosim有单独分开使用，也有同时出现的情况。在实际应用中，如果两种检验结果都与预期一致，那么可以两种检验结果都呈现，在丰富文章内容的同时，还能更加说明分组的合理性。但由于两种检验模型不一致，若出现一种检验是分组有差异，一种没有，择优而选就行。
2）两种检验方法计算原理比较繁琐，并且与不同距离类型（Bray-Curtis、Jaccard、Unifrac）搭配，输出的结果可能不一致，也许一次分析要花费不少时间，才能达到理想的结果，那么有高效率的解决方法吗？有的，给大家推荐基迪奥的在线平台，只要把简单的物种、otu丰度数据导进去，分分钟就能出结果，还能一键切换距离类型，减少试错和时间成本。
