NLP（四十二）：胶囊网络实现文本分类

一、理论学习

1、胶囊结构

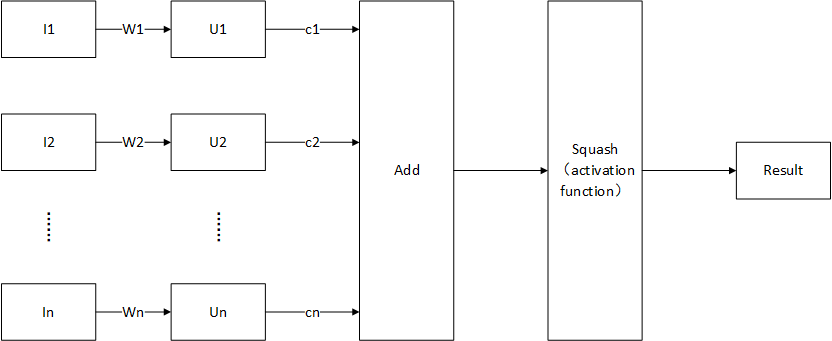
胶囊可以看成一种向量化的神经元。对于单个神经元而言，目前的深度网络中流动的数据均为标量。例如多层感知机的某一个神经元，其输入为若干个标量，输出为一个标量（不考虑批处理）；而对于胶囊而言，每个神经元输入为若干个向量，输出为一个向量（不考虑批处理）。前向传播如下所示：

其中Ii为第i个输入（向量），Wi为第i个权值（矩阵），Ui为中间变量（向量），由输入和权值叉乘获得。ci为路由权值（标量），需要注意的是该标量是前向传播过程中决定（使用动态路由算法）的，不是通过反向传播优化的参数。Squash为一种激活函数。前向传播使用公式表示如下所示：

Ui=WiT×IiS=∑i=0nci⋅UiResult=Squash(S)=||S||21+||S||2⋅S||S||

由以上可以看出，胶囊结构中流动的数据类型为向量，其激活函数Squash输入一个向量，输出一个向量。

2、 动态路由算法

动态路由算法适用于确定胶囊结构中ci的算法，其算法伪代码如下所示：

首先其输入为Uj|i为本层的中间变量，其中i为这一层胶囊数量，j为下一层胶囊数量，最终获得的胶囊的输出vj，其步骤描述如下：

1. 初始化：初始化一个临时变量b，为一个i×j的全为0的矩阵
2. 获取这一步的连接权值c：ci=softmax(bi)，将临时变量b通过softmax，保证ci的各分量和为1
3. 获取这一步的加权和结果S：$sj = \sum_i c{ij}u_{j|i}$，按这一步连接权值计算加权和
4. 非线性激活：vj=squash(sj)，经过非线性激活函数，获取这一步的胶囊输出
5. 迭代临时变量：$b{ij} = b{ij} + u{i|j} \cdot v{j}$，所这一步的输出与中间变量方向相近，增加临时变量b，即增加权值；若这一步输出与中间变量方向相反，减小临时变量b，即减小权值。
6. 若已经迭代到指定次数，输出vj，否侧跳到步骤2

同时，对于迭代次数j，论文中表示过多的迭代会导致过拟合，实践中建议使用3次迭代。

3、输出与代价函数

输出层胶囊的输出为向量，该向量的长度即为概率。也就是说，前向传播的结果为输出最长向量的输出胶囊所代表的结果。反向传播时，也需要考虑网络的输出为向量而不是标量，因此原论文中了如下的代价函数（每个输出的代价函数，代价函数为所有输出代价函数的和L=∑c=0nLc）

Lc=Tcmax(0,m+−||Vc||)2+λ(1−Tc)max(0,||vc||−m−)2

其中，Tc为标量，当分类结果为c时Tc=1，否则Tc=0；λ为固定值（一般为0.5），用于保证数值稳定性；m+和m−也为固定值：

• 对于Tc=1的输出胶囊，当输出向量大于m+时，代价函数为0，否则不为0
• 对于Tc=0的输出胶囊，当输出向量小于m−时，代价函数为0，否则不为0

4、整体架构

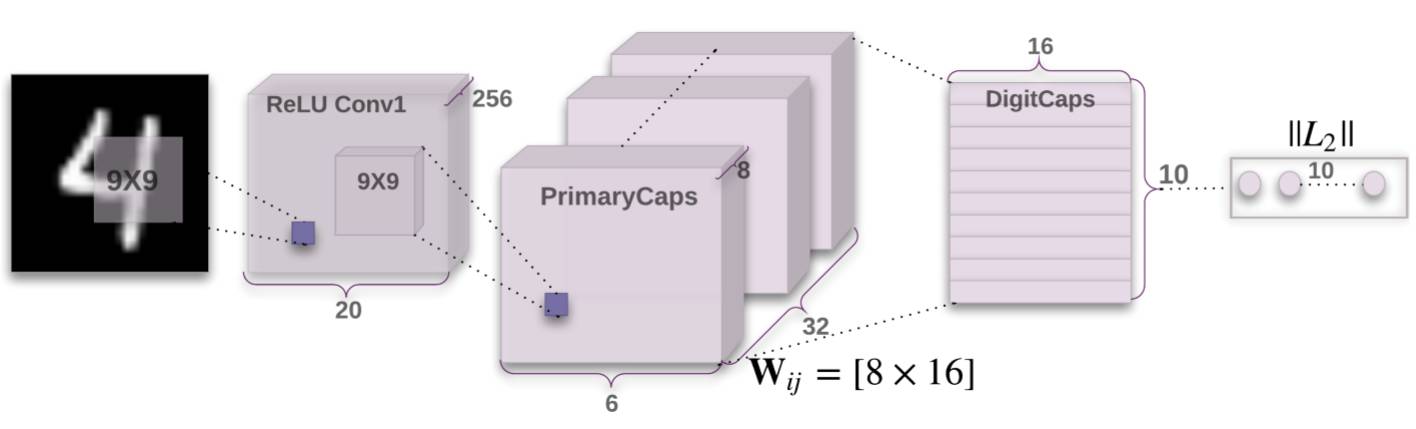
原论文中使举了一个识别MNIST手写数字数据集的例子，网络架构如下图所示：

• 第一层为普通的卷积层，使用9*9卷积，输出通道数为256，输出数据尺寸为20*20*256
• 第二层为卷积层，该卷积层由平行的32个卷积层组成，每个卷积层对应向量数据中的一个向量。每个卷积层均为9*9*256*8（输入channel为256，输出channel为8）。因此输出为6*6*32*8，即窗口大小为6*6，输出channel为32，每个数据为8个分量的向量。
• 第三层为胶囊层，行为类似于全连接层。输入为6*6*32=1152个8分量输入向量，输出为10个16分量的向量，对应的有1152*10个权值，每个权值为8*16的矩阵，最终输出为10个16分量的向量
• 最终输出10个16分量的向量，最终的分类结果是向量长度最大的输出。

二、代码阅读（PyTorch）

本次代码阅读并不关心具体的实现方式，主要阅读CapsNet的实现思路

1、前胶囊层（卷积层）

PYTHON

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

class PrimaryCaps(nn.Module): def __init__(self, num_capsules=8, in_channels=256, out_channels=32, kernel_size=9): super(PrimaryCaps, self).__init__() self.capsules = nn.ModuleList([ nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=2, padding=0) for _ in range(num_capsules)]) def forward(self, x): u = [capsule(x) for capsule in self.capsules] u = torch.stack(u, dim=1) u = u.view(x.size(0), 32 * 6 * 6, -1) return self.squash(u) def squash(self, input_tensor): squared_norm = (input_tensor ** 2).sum(-1, keepdim=True) output_tensor = squared_norm * input_tensor / ((1. + squared_norm) * torch.sqrt(squared_norm)) return output_tensor

重点关注forward前向传播部分：

PYTHON

1 2 3 4 5

def forward(self, x): u = [capsule(x) for capsule in self.capsules] u = torch.stack(u, dim=1) u = u.view(x.size(0), 32 * 6 * 6, -1) return self.squash(u)

self.capsules为num_capsules个[in_channels,out_channels,kernel_size,kernel_size]的卷积层，对应上文所述的第二层卷积层的操作。注意该部分的输出直接被变为[batch size,1152,8]的形式，且通过squash激活函数挤压输出向量

2、胶囊层

PYTHON

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

class DigitCaps(nn.Module): def __init__(self, num_capsules=10, num_routes=32 * 6 * 6, in_channels=8, out_channels=16): super(DigitCaps, self).__init__() self.in_channels = in_channels self.num_routes = num_routes self.num_capsules = num_capsules self.W = nn.Parameter(torch.randn(1, num_routes, num_capsules, out_channels, in_channels)) def forward(self, x): batch_size = x.size(0) x = torch.stack([x] * self.num_capsules, dim=2).unsqueeze(4) W = torch.cat([self.W] * batch_size, dim=0) u_hat = torch.matmul(W, x) b_ij = Variable(torch.zeros(1, self.num_routes, self.num_capsules, 1)) if USE_CUDA: b_ij = b_ij.cuda() num_iterations = 3 for iteration in range(num_iterations): c_ij = F.softmax(b_ij) c_ij = torch.cat([c_ij] * batch_size, dim=0).unsqueeze(4) s_j = (c_ij * u_hat).sum(dim=1, keepdim=True) v_j = self.squash(s_j) if iteration < num_iterations - 1: a_ij = torch.matmul(u_hat.transpose(3, 4), torch.cat([v_j] * self.num_routes, dim=1)) b_ij = b_ij + a_ij.squeeze(4).mean(dim=0, keepdim=True) return v_j.squeeze(1) def squash(self, input_tensor): squared_norm = (input_tensor ** 2).sum(-1, keepdim=True) output_tensor = squared_norm * input_tensor / ((1. + squared_norm) * torch.sqrt(squared_norm)) return output_tensor

获得中间向量

PYTHON

1 2 3 4 5

batch_size = x.size(0) x = torch.stack([x] * self.num_capsules, dim=2).unsqueeze(4) W = torch.cat([self.W] * batch_size, dim=0) u_hat = torch.matmul(W, x)

这一部分计算中间向量Ui

动态路由

PYTHON

1 2 3 4 5 6 7 8 9 10

for iteration in range(num_iterations): c_ij = F.softmax(b_ij) c_ij = torch.cat([c_ij] * batch_size, dim=0).unsqueeze(4) s_j = (c_ij * u_hat).sum(dim=1, keepdim=True) v_j = self.squash(s_j) if iteration < num_iterations - 1: a_ij = torch.matmul(u_hat.transpose(3, 4), torch.cat([v_j] * self.num_routes, dim=1)) b_ij = b_ij + a_ij.squeeze(4).mean(dim=0, keepdim=True)

动态路由的结构中：

• 第1行计算了softmax函数的结果，对用临时变量b
• 第5行计算加权和
• 第6行计算当前迭代次数的输出
• 第9和10行更新临时向量的值

代价函数

PYTHON

1 2 3 4 5 6 7 8

def margin_loss(self, x, labels, size_average=True): batch_size = x.size(0) v_c = torch.sqrt((x**2).sum(dim=2, keepdim=True)) left = F.relu(0.9 - v_c).view(batch_size, -1) right = F.relu(v_c - 0.1).view(batch_size, -1) loss = labels * left + 0.5 * (1.0 - labels) * right loss = loss.sum(dim=1).mean() return loss

该函数为代价函数，分别实现了两种情况下(Tc=0,Tc=1)的代价函数。

三、参考资料

代码来自higgsfield’s github

文字资料参考weakish翻译的Max Pechyonkin的博客：

• CapsNet入门系列之一：胶囊网络背后的直觉
• CapsNet入门系列之二：胶囊如何工作
• CapsNet入门系列之三：囊间动态路由算法
• CapsNet入门系列之四：胶囊网络架构

此外还参考：

• 机器之心：先读懂CapsNet架构然后用TensorFlow实现，这应该是最详细的教程了
• 机器之心：Capsule官方代码开源之后，机器之心做了份核心代码解读

四、CapsNet基本结构

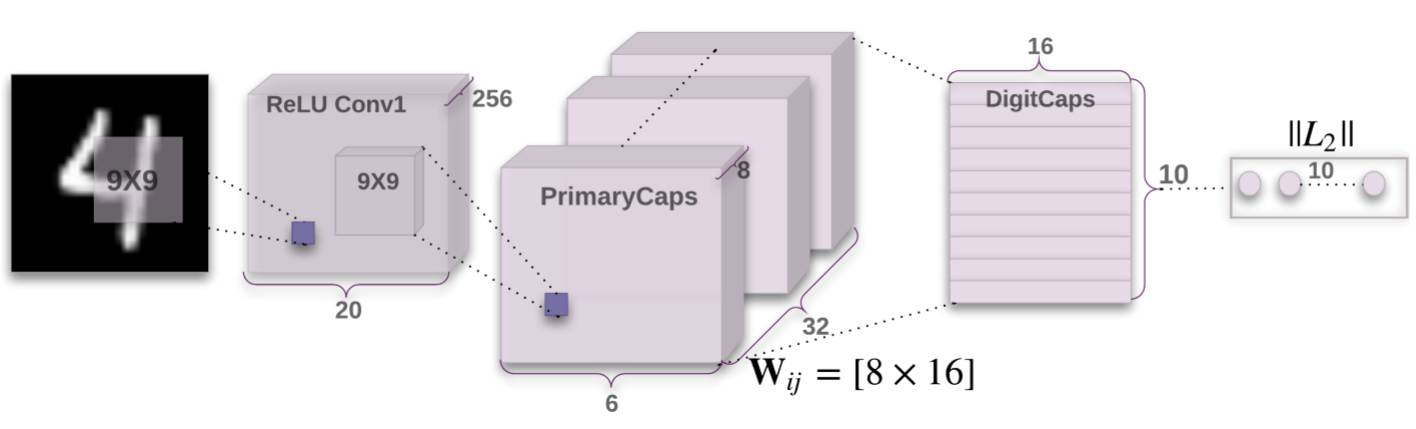
参考CapsNet的论文，提出的基本结构如下所示：

可以看出，CapsNet的基本结构如下所示：

• 普通卷积层Conv1：基本的卷积层，感受野较大，达到了9x9
• 预胶囊层PrimaryCaps：为胶囊层准备，运算为卷积运算，最终输出为[batch,caps_num,caps_length]的三维数据：
  • batch为批大小
  • caps_num为胶囊的数量
  • caps_length为每个胶囊的长度（每个胶囊为一个向量，该向量包括caps_length个分量）
• 胶囊层DigitCaps：胶囊层，目的是代替最后一层全连接层，输出为10个胶囊

五、代码实现

1、胶囊相关组件

激活函数Squash

胶囊网络有特有的激活函数Squash函数：

Squash(S)=||S||21+||S||2⋅S||S||

其中输入为S胶囊，该激活函数可以将胶囊的长度压缩，代码实现如下：

PYTHON

1 2 3 4

def squash(inputs, axis=-1): norm = torch.norm(inputs, p=2, dim=axis, keepdim=True) scale = norm**2 / (1 + norm**2) / (norm + 1e-8) return scale * inputs

其中：

• norm = torch.norm(inputs, p=2, dim=axis, keepdim=True)计算输入胶囊的长度，p=2表示计算的是二范数，keepdim=True表示保持原有的空间形状。
• scale = norm**2 / (1 + norm**2) / (norm + 1e-8)计算缩放因子，即||S||21+||S||2⋅1||S||
• return scale * inputs完成计算

预胶囊层PrimaryCaps

PYTHON

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

class PrimaryCapsule(nn.Module): """ Apply Conv2D with `out_channels` and then reshape to get capsules :param in_channels: input channels :param out_channels: output channels :param dim_caps: dimension of capsule :param kernel_size: kernel size :return: output tensor, size=[batch, num_caps, dim_caps] """ def __init__(self, in_channels, out_channels, dim_caps, kernel_size, stride=1, padding=0): super(PrimaryCapsule, self).__init__() self.dim_caps = dim_caps self.conv2d = nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size, stride=stride, padding=padding) def forward(self, x): outputs = self.conv2d(x) outputs = outputs.view(x.size(0), -1, self.dim_caps) return squash(outputs)

预胶囊层使用卷积层实现，其前向传播包括三个部分：

• outputs = self.conv2d(x)：对输入进行卷积处理，这一步output的形状是[batch,out_channels,p_w,p_h]
• outputs = outputs.view(x.size(0), -1, self.dim_caps)：将4D的卷积输出变为3D的胶囊输出形式，output的形状为[batch,caps_num,dim_caps]，其中caps_num为胶囊数量，可自动计算；dim_caps为胶囊长度，需要预先指定。
• return squash(outputs)：激活函数，并返回激活后的胶囊

胶囊层DigitCaps

参数定义

PYTHON

1 2 3 4 5 6 7 8

def __init__(self, in_num_caps, in_dim_caps, out_num_caps, out_dim_caps, routings=3): super(DenseCapsule, self).__init__() self.in_num_caps = in_num_caps self.in_dim_caps = in_dim_caps self.out_num_caps = out_num_caps self.out_dim_caps = out_dim_caps self.routings = routings self.weight = nn.Parameter(0.01 * torch.randn(out_num_caps, in_num_caps, out_dim_caps, in_dim_caps))

参数定义如下：

• in_num_caps：输入胶囊的数量
• in_dim_caps：输入胶囊的长度（维数）
• out_num_caps：输出胶囊的数量
• out_dim_caps：输出胶囊的长度（维数）
• routings：动态路由迭代的次数

另外，还定义了权值weight，尺寸为[out_num_caps, in_num_caps, out_dim_caps, in_dim_caps]，即每个输出和每个输出胶囊都有连接

前向传播

PYTHON

1 2 3 4 5 6 7 8 9 10 11 12 13 14

def forward(self, x): x_hat = torch.squeeze(torch.matmul(self.weight, x[:, None, :, :, None]), dim=-1) x_hat_detached = x_hat.detach() b = Variable(torch.zeros(x.size(0), self.out_num_caps, self.in_num_caps)).cuda() assert self.routings > 0, 'The \'routings\' should be > 0.' for i in range(self.routings): c = F.softmax(b, dim=1) if i == self.routings - 1: outputs = squash(torch.sum(c[:, :, :, None] * x_hat, dim=-2, keepdim=True)) else: outputs = squash(torch.sum(c[:, :, :, None] * x_hat_detached, dim=-2, keepdim=True)) b = b + torch.sum(outputs * x_hat_detached, dim=-1) return torch.squeeze(outputs, dim=-2)

前向传播分为两个部分：输入映射和动态路由。输入映射如下所示：

1. x_hat = torch.squeeze(torch.matmul(self.weight, x[:, None, :, :, None]), dim=-1)
   • x[:, None, :, :, None]将数据维度从[batch, in_num_caps, in_dim_caps]扩展到[batch, 1,in_num_caps, in_dim_caps,1]
   • torch.matmul()将weight和扩展后的输入相乘，weight的尺寸是[out_num_caps, in_num_caps, out_dim_caps, in_dim_caps]，相乘后结果尺寸为[batch, out_num_caps, in_num_caps,out_dim_caps, 1]
   • torch.squeeze()去除多余的维度，去除后结果尺寸[batch,out_num_caps,in_num_caps,out_dim_caps]
2. x_hat_detached = x_hat.detach()截断梯度反向传播

这一部分结束后，每个输入胶囊都产生了out_num_caps个输出胶囊，所以目前共有in_num_caps*out_num_caps个胶囊，第二部分是动态路由，动态路由的算法图如下所示：

以下部分实现了该过程：

PYTHON

1 2 3 4 5 6 7 8

b = Variable(torch.zeros(x.size(0), self.out_num_caps, self.in_num_caps)).cuda() for i in range(self.routings): c = F.softmax(b, dim=1) if i == self.routings - 1: outputs = squash(torch.sum(c[:, :, :, None] * x_hat, dim=-2, keepdim=True)) else: outputs = squash(torch.sum(c[:, :, :, None] * x_hat_detached, dim=-2, keepdim=True)) b = b + torch.sum(outputs * x_hat_detached, dim=-1)

1. 第一部分是softmax函数，使用c = F.softmax(b, dim=1)实现，该步骤不改变b的尺寸
2. 第二部分是计算路由结果：outputs = squash(torch.sum(c[:, :, :, None] * x_hat, dim=-2, keepdim=True))
   • c[:, :, :, None]扩展c的维度，以便按位置相乘时广播维度
   • torch.sum(c[:, :, :, None] * x_hat, dim=-2, keepdim=True)计算出每个胶囊与对应权值的积，即算法中的sj，同时在倒数第二维上求和，则该步输出的结果尺寸为[batch, out_num_caps, 1,out_dim_caps]
   • 通过激活函数squash()
3. 第三部分更新权重b = b + torch.sum(outputs * x_hat_detached, dim=-1)，两个按位相乘的变量尺寸分别为[batch, out_num_caps, in_num_caps, out_dim_caps]和[batch, out_num_caps, 1,out_dim_caps]，倒数第二维上有广播行为，因此最终结果为[batch, out_num_caps, in_num_caps]

2、其他组件

网络结构

PYTHON

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48

class CapsuleNet(nn.Module): """ A Capsule Network on MNIST. :param input_size: data size = [channels, width, height] :param classes: number of classes :param routings: number of routing iterations Shape: - Input: (batch, channels, width, height), optional (batch, classes) . - Output:((batch, classes), (batch, channels, width, height)) """ def __init__(self, input_size, classes, routings): super(CapsuleNet, self).__init__() self.input_size = input_size self.classes = classes self.routings = routings # Layer 1: Just a conventional Conv2D layer self.conv1 = nn.Conv2d(input_size[0], 256, kernel_size=9, stride=1, padding=0) # Layer 2: Conv2D layer with `squash` activation, then reshape to [None, num_caps, dim_caps] self.primarycaps = PrimaryCapsule(256, 256, 8, kernel_size=9, stride=2, padding=0) # Layer 3: Capsule layer. Routing algorithm works here. self.digitcaps = DenseCapsule(in_num_caps=32*6*6, in_dim_caps=8, out_num_caps=classes, out_dim_caps=16, routings=routings) # Decoder network. self.decoder = nn.Sequential( nn.Linear(16*classes, 512), nn.ReLU(inplace=True), nn.Linear(512, 1024), nn.ReLU(inplace=True), nn.Linear(1024, input_size[0] * input_size[1] * input_size[2]), nn.Sigmoid() ) self.relu = nn.ReLU() def forward(self, x, y=None): x = self.relu(self.conv1(x)) x = self.primarycaps(x) x = self.digitcaps(x) length = x.norm(dim=-1) if y is None: # during testing, no label given. create one-hot coding using `length` index = length.max(dim=1)[1] y = Variable(torch.zeros(length.size()).scatter_(1, index.view(-1, 1).cpu().data, 1.).cuda()) reconstruction = self.decoder((x * y[:, :, None]).view(x.size(0), -1)) return length, reconstruction.view(-1, *self.input_size)

网络组件包括两个部分：胶囊网络和重建网络，重建网络为多层感知机，根据胶囊的结果重建了图像，这表示胶囊除了包括结果外，还可以包括一些空间信息。

注意胶囊网络的前向传播部分为：

PYTHON

1 2 3 4

x = self.relu(self.conv1(x)) x = self.primarycaps(x) x = self.digitcaps(x) length = x.norm(dim=-1)

最终的输出为每个胶囊的二范数，即向量的长度

代价函数

胶囊神经网络的胶囊部分的代价函数如下所示

Lc=Tcmax(0,m+−||Vc||)2+λ(1−Tc)max(0,||vc||−m−)2

以下代码实现了这个部分，其中L为胶囊的代价函数计算，这里m+=0.9,m−=0.1，L_recon为重建的代价函数，为输入图像与复原图像的MSELoss函数。

PYTHON

1 2 3 4 5 6

def caps_loss(y_true, y_pred, x, x_recon, lam_recon): L = y_true * torch.clamp(0.9 - y_pred, min=0.) ** 2 + \ 0.5 * (1 - y_true) * torch.clamp(y_pred - 0.1, min=0.) ** 2 L_margin = L.sum(dim=1).mean() L_recon = nn.MSELoss()(x_recon, x) return L_margin + lam_recon * L_recon

六、参考

CapsNet论文

CapsNet开源代码

七、代码实战

1、假设文本的batch_size=32, 通道为1，40个字，每个字embedding_dim=200。

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable


def squash(inputs, axis=-1):
    """
    The non-linear activation used in Capsule. It drives the length of a large vector to near 1 and small vector to 0
    :param inputs: vectors to be squashed
    :param axis: the axis to squash
    :return: a Tensor with same size as inputs
    """
    norm = torch.norm(inputs, p=2, dim=axis, keepdim=True)
    scale = norm**2 / (1 + norm**2) / (norm + 1e-8)
    return scale * inputs


class DenseCapsule(nn.Module):
    """
    The dense capsule layer. It is similar to Dense (FC) layer. Dense layer has `in_num` inputs, each is a scalar, the
    output of the neuron from the former layer, and it has `out_num` output neurons. DenseCapsule just expands the
    output of the neuron from scalar to vector. So its input size = [None, in_num_caps, in_dim_caps] and output size = \
    [None, out_num_caps, out_dim_caps]. For Dense Layer, in_dim_caps = out_dim_caps = 1.

    :param in_num_caps: number of cpasules inputted to this layer
    :param in_dim_caps: dimension of input capsules
    :param out_num_caps: number of capsules outputted from this layer
    :param out_dim_caps: dimension of output capsules
    :param routings: number of iterations for the routing algorithm
    """
    def __init__(self, in_num_caps, in_dim_caps, out_num_caps, out_dim_caps, routings=3):
        super(DenseCapsule, self).__init__()
        self.in_num_caps = in_num_caps
        self.in_dim_caps = in_dim_caps
        self.out_num_caps = out_num_caps
        self.out_dim_caps = out_dim_caps
        self.routings = routings
        self.weight = nn.Parameter(0.01 * torch.randn(out_num_caps, in_num_caps, out_dim_caps, in_dim_caps))

    def forward(self, x):
        print(x.shape) #[32, 32, 8]
        print(x[:, None, :, :, None].shape) #[32, 1, 32, 8, 1]
        print(self.weight.shape) #[203, 1152, 16, 8]
        # x.size=[batch, in_num_caps, in_dim_caps]
        # expanded to    [batch, 1,            in_num_caps, in_dim_caps,  1]
        # weight.size   =[       out_num_caps, in_num_caps, out_dim_caps, in_dim_caps]
        # torch.matmul: [out_dim_caps, in_dim_caps] x [in_dim_caps, 1] -> [out_dim_caps, 1]
        # => x_hat.size =[batch, out_num_caps, in_num_caps, out_dim_caps]
        x_hat = torch.squeeze(torch.matmul(self.weight, x[:, None, :, :, None]), dim=-1)

        # In forward pass, `x_hat_detached` = `x_hat`;
        # In backward, no gradient can flow from `x_hat_detached` back to `x_hat`.
        x_hat_detached = x_hat.detach()

        # The prior for coupling coefficient, initialized as zeros.
        # b.size = [batch, out_num_caps, in_num_caps]
        b = Variable(torch.zeros(x.size(0), self.out_num_caps, self.in_num_caps))

        assert self.routings > 0, 'The \'routings\' should be > 0.'
        for i in range(self.routings):
            # c.size = [batch, out_num_caps, in_num_caps]
            c = F.softmax(b, dim=1)

            # At last iteration, use `x_hat` to compute `outputs` in order to backpropagate gradient
            if i == self.routings - 1:
                # c.size expanded to [batch, out_num_caps, in_num_caps, 1           ]
                # x_hat.size     =   [batch, out_num_caps, in_num_caps, out_dim_caps]
                # => outputs.size=   [batch, out_num_caps, 1,           out_dim_caps]
                outputs = squash(torch.sum(c[:, :, :, None] * x_hat, dim=-2, keepdim=True))
                # outputs = squash(torch.matmul(c[:, :, None, :], x_hat))  # alternative way
            else:  # Otherwise, use `x_hat_detached` to update `b`. No gradients flow on this path.
                outputs = squash(torch.sum(c[:, :, :, None] * x_hat_detached, dim=-2, keepdim=True))
                # outputs = squash(torch.matmul(c[:, :, None, :], x_hat_detached))  # alternative way

                # outputs.size       =[batch, out_num_caps, 1,           out_dim_caps]
                # x_hat_detached.size=[batch, out_num_caps, in_num_caps, out_dim_caps]
                # => b.size          =[batch, out_num_caps, in_num_caps]
                b = b + torch.sum(outputs * x_hat_detached, dim=-1)

        return torch.squeeze(outputs, dim=-2)


class PrimaryCapsule(nn.Module):
    """
    Apply Conv2D with `out_channels` and then reshape to get capsules
    :param in_channels: input channels
    :param out_channels: output channels
    :param dim_caps: dimension of capsule
    :param kernel_size: kernel size
    :return: output tensor, size=[batch, num_caps, dim_caps]
    """
    def __init__(self, in_channels, out_channels, dim_caps, kernel_size, stride=1, padding=0):
        super(PrimaryCapsule, self).__init__()
        self.dim_caps = dim_caps
        self.conv2d = nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size, stride=stride, padding=padding)

    def forward(self, x):
        print(x.shape) #[32, 256, 37, 1]
        outputs = self.conv2d(x)
        outputs = outputs.view(x.size(0), -1, self.dim_caps)
        return squash(outputs)

class CapsuleNet(nn.Module):
    """
    A Capsule Network on MNIST.
    :param input_size: data size = [channels, width, height]
    :param classes: number of classes
    :param routings: number of routing iterations
    Shape:
        - Input: (batch, channels, width, height), optional (batch, classes) .
        - Output:((batch, classes), (batch, channels, width, height))
    """
    def __init__(self, input_size, classes, routings):
        super(CapsuleNet, self).__init__()
        self.input_size = input_size
        self.classes = classes
        self.routings = routings

        # Layer 1: Just a conventional Conv2D layer
        self.conv1 = nn.Conv2d(input_size[0], 256, kernel_size=(4, 200), stride=1, padding=0)

        # Layer 2: Conv2D layer with `squash` activation, then reshape to [None, num_caps, dim_caps]
        self.primarycaps = PrimaryCapsule(256, 256, 8, kernel_size=(37, 1), stride=2, padding=0)

        # Layer 3: Capsule layer. Routing algorithm works here.
        self.digitcaps = DenseCapsule(in_num_caps=32, in_dim_caps=8,
                                      out_num_caps=classes, out_dim_caps=16, routings=routings)

        # Decoder network.
        self.decoder = nn.Sequential(
            nn.Linear(16*classes, 512),
            nn.ReLU(inplace=True),
            nn.Linear(512, 1024),
            nn.ReLU(inplace=True),
            nn.Linear(1024, input_size[0] * input_size[1] * input_size[2]),
            nn.Sigmoid()
        )

        self.relu = nn.ReLU()

    def forward(self, x, y=None):
        x = self.relu(self.conv1(x))
        x = self.primarycaps(x)
        x = self.digitcaps(x)
        length = x.norm(dim=-1)
        if y is None:  # during testing, no label given. create one-hot coding using `length`
            index = length.max(dim=1)[1]
            y = Variable(torch.zeros(length.size()).scatter_(1, index.view(-1, 1).cpu().data, 1.))
        reconstruction = self.decoder((x * y[:, :, None]).view(x.size(0), -1))
        return length, reconstruction.view(-1, *self.input_size)

if __name__ == '__main__':
    x = torch.rand([16, 1, 40, 200])
    m = CapsuleNet([1, 40, 200], 203, 3)
    y_pred, x_recon = m(x)
    print(y_pred.shape)

2、官方的训练代码，仅供参考

"""
Pytorch implementation of CapsNet in paper Dynamic Routing Between Capsules.
The current version maybe only works for TensorFlow backend. Actually it will be straightforward to re-write to TF code.
Adopting to other backends should be easy, but I have not tested this.

Usage:
       Launch `python CapsNet.py -h` for usage help

Result:
    Validation accuracy > 99.6% after 50 epochs.
    Speed: About 73s/epoch on a single GTX1070 GPU card and 43s/epoch on a GTX1080Ti GPU.

Author: Xifeng Guo, E-mail: `guoxifeng1990@163.com`, Github: `https://github.com/XifengGuo/CapsNet-Pytorch`
"""

import torch
from torch import nn
from torch.optim import Adam, lr_scheduler
from torch.autograd import Variable
from torchvision import transforms, datasets
from capsulelayers import DenseCapsule, PrimaryCapsule


class CapsuleNet(nn.Module):
    """
    A Capsule Network on MNIST.
    :param input_size: data size = [channels, width, height]
    :param classes: number of classes
    :param routings: number of routing iterations
    Shape:
        - Input: (batch, channels, width, height), optional (batch, classes) .
        - Output:((batch, classes), (batch, channels, width, height))
    """
    def __init__(self, input_size, classes, routings):
        super(CapsuleNet, self).__init__()
        self.input_size = input_size
        self.classes = classes
        self.routings = routings

        # Layer 1: Just a conventional Conv2D layer
        self.conv1 = nn.Conv2d(input_size[0], 256, kernel_size=9, stride=1, padding=0)

        # Layer 2: Conv2D layer with `squash` activation, then reshape to [None, num_caps, dim_caps]
        self.primarycaps = PrimaryCapsule(256, 256, 8, kernel_size=9, stride=2, padding=0)

        # Layer 3: Capsule layer. Routing algorithm works here.
        self.digitcaps = DenseCapsule(in_num_caps=32*6*6, in_dim_caps=8,
                                      out_num_caps=classes, out_dim_caps=16, routings=routings)

        # Decoder network.
        self.decoder = nn.Sequential(
            nn.Linear(16*classes, 512),
            nn.ReLU(inplace=True),
            nn.Linear(512, 1024),
            nn.ReLU(inplace=True),
            nn.Linear(1024, input_size[0] * input_size[1] * input_size[2]),
            nn.Sigmoid()
        )

        self.relu = nn.ReLU()

    def forward(self, x, y=None):
        x = self.relu(self.conv1(x))
        x = self.primarycaps(x)
        x = self.digitcaps(x)
        length = x.norm(dim=-1)
        if y is None:  # during testing, no label given. create one-hot coding using `length`
            index = length.max(dim=1)[1]
            y = Variable(torch.zeros(length.size()).scatter_(1, index.view(-1, 1).cpu().data, 1.).cuda())
        reconstruction = self.decoder((x * y[:, :, None]).view(x.size(0), -1))
        return length, reconstruction.view(-1, *self.input_size)


def caps_loss(y_true, y_pred, x, x_recon, lam_recon):
    """
    Capsule loss = Margin loss + lam_recon * reconstruction loss.
    :param y_true: true labels, one-hot coding, size=[batch, classes]
    :param y_pred: predicted labels by CapsNet, size=[batch, classes]
    :param x: input data, size=[batch, channels, width, height]
    :param x_recon: reconstructed data, size is same as `x`
    :param lam_recon: coefficient for reconstruction loss
    :return: Variable contains a scalar loss value.
    """
    L = y_true * torch.clamp(0.9 - y_pred, min=0.) ** 2 + \
        0.5 * (1 - y_true) * torch.clamp(y_pred - 0.1, min=0.) ** 2
    L_margin = L.sum(dim=1).mean()

    L_recon = nn.MSELoss()(x_recon, x)

    return L_margin + lam_recon * L_recon


def show_reconstruction(model, test_loader, n_images, args):
    import matplotlib.pyplot as plt
    from utils import combine_images
    from PIL import Image
    import numpy as np

    model.eval()
    for x, _ in test_loader:
        x = Variable(x[:min(n_images, x.size(0))].cuda(), volatile=True)
        _, x_recon = model(x)
        data = np.concatenate([x.data, x_recon.data])
        img = combine_images(np.transpose(data, [0, 2, 3, 1]))
        image = img * 255
        Image.fromarray(image.astype(np.uint8)).save(args.save_dir + "/real_and_recon.png")
        print()
        print('Reconstructed images are saved to %s/real_and_recon.png' % args.save_dir)
        print('-' * 70)
        plt.imshow(plt.imread(args.save_dir + "/real_and_recon.png", ))
        plt.show()
        break


def test(model, test_loader, args):
    model.eval()
    test_loss = 0
    correct = 0
    for x, y in test_loader:
        y = torch.zeros(y.size(0), 10).scatter_(1, y.view(-1, 1), 1.)
        x, y = Variable(x.cuda(), volatile=True), Variable(y.cuda())
        y_pred, x_recon = model(x)
        test_loss += caps_loss(y, y_pred, x, x_recon, args.lam_recon).data[0] * x.size(0)  # sum up batch loss
        y_pred = y_pred.data.max(1)[1]
        y_true = y.data.max(1)[1]
        correct += y_pred.eq(y_true).cpu().sum()

    test_loss /= len(test_loader.dataset)
    return test_loss, correct / len(test_loader.dataset)


def train(model, train_loader, test_loader, args):
    """
    Training a CapsuleNet
    :param model: the CapsuleNet model
    :param train_loader: torch.utils.data.DataLoader for training data
    :param test_loader: torch.utils.data.DataLoader for test data
    :param args: arguments
    :return: The trained model
    """
    print('Begin Training' + '-'*70)
    from time import time
    import csv
    logfile = open(args.save_dir + '/log.csv', 'w')
    logwriter = csv.DictWriter(logfile, fieldnames=['epoch', 'loss', 'val_loss', 'val_acc'])
    logwriter.writeheader()

    t0 = time()
    optimizer = Adam(model.parameters(), lr=args.lr)
    lr_decay = lr_scheduler.ExponentialLR(optimizer, gamma=args.lr_decay)
    best_val_acc = 0.
    for epoch in range(args.epochs):
        model.train()  # set to training mode
        lr_decay.step()  # decrease the learning rate by multiplying a factor `gamma`
        ti = time()
        training_loss = 0.0
        for i, (x, y) in enumerate(train_loader):  # batch training
            y = torch.zeros(y.size(0), 10).scatter_(1, y.view(-1, 1), 1.)  # change to one-hot coding
            x, y = Variable(x.cuda()), Variable(y.cuda())  # convert input data to GPU Variable

            optimizer.zero_grad()  # set gradients of optimizer to zero
            y_pred, x_recon = model(x, y)  # forward
            loss = caps_loss(y, y_pred, x, x_recon, args.lam_recon)  # compute loss
            loss.backward()  # backward, compute all gradients of loss w.r.t all Variables
            training_loss += loss.data[0] * x.size(0)  # record the batch loss
            optimizer.step()  # update the trainable parameters with computed gradients

        # compute validation loss and acc
        val_loss, val_acc = test(model, test_loader, args)
        logwriter.writerow(dict(epoch=epoch, loss=training_loss / len(train_loader.dataset),
                                val_loss=val_loss, val_acc=val_acc))
        print("==> Epoch %02d: loss=%.5f, val_loss=%.5f, val_acc=%.4f, time=%ds"
              % (epoch, training_loss / len(train_loader.dataset),
                 val_loss, val_acc, time() - ti))
        if val_acc > best_val_acc:  # update best validation acc and save model
            best_val_acc = val_acc
            torch.save(model.state_dict(), args.save_dir + '/epoch%d.pkl' % epoch)
            print("best val_acc increased to %.4f" % best_val_acc)
    logfile.close()
    torch.save(model.state_dict(), args.save_dir + '/trained_model.pkl')
    print('Trained model saved to \'%s/trained_model.h5\'' % args.save_dir)
    print("Total time = %ds" % (time() - t0))
    print('End Training' + '-' * 70)
    return model


def load_mnist(path='./data', download=False, batch_size=100, shift_pixels=2):
    """
    Construct dataloaders for training and test data. Data augmentation is also done here.
    :param path: file path of the dataset
    :param download: whether to download the original data
    :param batch_size: batch size
    :param shift_pixels: maximum number of pixels to shift in each direction
    :return: train_loader, test_loader
    """
    kwargs = {'num_workers': 1, 'pin_memory': True}

    train_loader = torch.utils.data.DataLoader(
        datasets.MNIST(path, train=True, download=download,
                       transform=transforms.Compose([transforms.RandomCrop(size=28, padding=shift_pixels),
                                                     transforms.ToTensor()])),
        batch_size=batch_size, shuffle=True, **kwargs)
    test_loader = torch.utils.data.DataLoader(
        datasets.MNIST(path, train=False, download=download,
                       transform=transforms.ToTensor()),
        batch_size=batch_size, shuffle=True, **kwargs)

    return train_loader, test_loader


if __name__ == "__main__":
    import argparse
    import os

    # setting the hyper parameters
    parser = argparse.ArgumentParser(description="Capsule Network on MNIST.")
    parser.add_argument('--epochs', default=50, type=int)
    parser.add_argument('--batch_size', default=100, type=int)
    parser.add_argument('--lr', default=0.001, type=float,
                        help="Initial learning rate")
    parser.add_argument('--lr_decay', default=0.9, type=float,
                        help="The value multiplied by lr at each epoch. Set a larger value for larger epochs")
    parser.add_argument('--lam_recon', default=0.0005 * 784, type=float,
                        help="The coefficient for the loss of decoder")
    parser.add_argument('-r', '--routings', default=3, type=int,
                        help="Number of iterations used in routing algorithm. should > 0")  # num_routing should > 0
    parser.add_argument('--shift_pixels', default=2, type=int,
                        help="Number of pixels to shift at most in each direction.")
    parser.add_argument('--data_dir', default='./data',
                        help="Directory of data. If no data, use \'--download\' flag to download it")
    parser.add_argument('--download', action='store_true',
                        help="Download the required data.")
    parser.add_argument('--save_dir', default='./result')
    parser.add_argument('-t', '--testing', action='store_true',
                        help="Test the trained model on testing dataset")
    parser.add_argument('-w', '--weights', default=None,
                        help="The path of the saved weights. Should be specified when testing")
    args = parser.parse_args()
    print(args)
    if not os.path.exists(args.save_dir):
        os.makedirs(args.save_dir)

    # load data
    train_loader, test_loader = load_mnist(args.data_dir, download=False, batch_size=args.batch_size)

    # define model
    model = CapsuleNet(input_size=[1, 28, 28], classes=10, routings=3)
    model.cuda()
    print(model)

    # train or test
    if args.weights is not None:  # init the model weights with provided one
        model.load_state_dict(torch.load(args.weights))
    if not args.testing:
        train(model, train_loader, test_loader, args)
    else:  # testing
        if args.weights is None:
            print('No weights are provided. Will test using random initialized weights.')
        test_loss, test_acc = test(model=model, test_loader=test_loader, args=args)
        print('test acc = %.4f, test loss = %.5f' % (test_acc, test_loss))
        show_reconstruction(model, test_loader, 50, args)

 

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
from torch.optim import Adam, lr_scheduler

def squash(inputs, axis=-1):
    """
    The non-linear activation used in Capsule. It drives the length of a large vector to near 1 and small vector to 0
    :param inputs: vectors to be squashed
    :param axis: the axis to squash
    :return: a Tensor with same size as inputs
    """
    norm = torch.norm(inputs, p=2, dim=axis, keepdim=True)
    scale = norm**2 / (1 + norm**2) / (norm + 1e-8)
    return scale * inputs


class DenseCapsule(nn.Module):
    """
    The dense capsule layer. It is similar to Dense (FC) layer. Dense layer has `in_num` inputs, each is a scalar, the
    output of the neuron from the former layer, and it has `out_num` output neurons. DenseCapsule just expands the
    output of the neuron from scalar to vector. So its input size = [None, in_num_caps, in_dim_caps] and output size = \
    [None, out_num_caps, out_dim_caps]. For Dense Layer, in_dim_caps = out_dim_caps = 1.

    :param in_num_caps: number of cpasules inputted to this layer
    :param in_dim_caps: dimension of input capsules
    :param out_num_caps: number of capsules outputted from this layer
    :param out_dim_caps: dimension of output capsules
    :param routings: number of iterations for the routing algorithm
    """
    def __init__(self, in_num_caps, in_dim_caps, out_num_caps, out_dim_caps, routings=3):
        super(DenseCapsule, self).__init__()
        self.in_num_caps = in_num_caps
        self.in_dim_caps = in_dim_caps
        self.out_num_caps = out_num_caps
        self.out_dim_caps = out_dim_caps
        self.routings = routings
        self.weight = nn.Parameter(0.01 * torch.randn(out_num_caps, in_num_caps, out_dim_caps, in_dim_caps))

    def forward(self, x):
        print(x.shape) #[32, 32, 8]
        print(x[:, None, :, :, None].shape) #[32, 1, 32, 8, 1]
        print(self.weight.shape) #[203, 1152, 16, 8]
        # x.size=[batch, in_num_caps, in_dim_caps]
        # expanded to    [batch, 1,            in_num_caps, in_dim_caps,  1]
        # weight.size   =[       out_num_caps, in_num_caps, out_dim_caps, in_dim_caps]
        # torch.matmul: [out_dim_caps, in_dim_caps] x [in_dim_caps, 1] -> [out_dim_caps, 1]
        # => x_hat.size =[batch, out_num_caps, in_num_caps, out_dim_caps]
        x_hat = torch.squeeze(torch.matmul(self.weight, x[:, None, :, :, None]), dim=-1)

        # In forward pass, `x_hat_detached` = `x_hat`;
        # In backward, no gradient can flow from `x_hat_detached` back to `x_hat`.
        x_hat_detached = x_hat.detach()

        # The prior for coupling coefficient, initialized as zeros.
        # b.size = [batch, out_num_caps, in_num_caps]
        b = Variable(torch.zeros(x.size(0), self.out_num_caps, self.in_num_caps))

        assert self.routings > 0, 'The \'routings\' should be > 0.'
        for i in range(self.routings):
            # c.size = [batch, out_num_caps, in_num_caps]
            c = F.softmax(b, dim=1)

            # At last iteration, use `x_hat` to compute `outputs` in order to backpropagate gradient
            if i == self.routings - 1:
                # c.size expanded to [batch, out_num_caps, in_num_caps, 1           ]
                # x_hat.size     =   [batch, out_num_caps, in_num_caps, out_dim_caps]
                # => outputs.size=   [batch, out_num_caps, 1,           out_dim_caps]
                outputs = squash(torch.sum(c[:, :, :, None] * x_hat, dim=-2, keepdim=True))
                # outputs = squash(torch.matmul(c[:, :, None, :], x_hat))  # alternative way
            else:  # Otherwise, use `x_hat_detached` to update `b`. No gradients flow on this path.
                outputs = squash(torch.sum(c[:, :, :, None] * x_hat_detached, dim=-2, keepdim=True))
                # outputs = squash(torch.matmul(c[:, :, None, :], x_hat_detached))  # alternative way

                # outputs.size       =[batch, out_num_caps, 1,           out_dim_caps]
                # x_hat_detached.size=[batch, out_num_caps, in_num_caps, out_dim_caps]
                # => b.size          =[batch, out_num_caps, in_num_caps]
                b = b + torch.sum(outputs * x_hat_detached, dim=-1)

        return torch.squeeze(outputs, dim=-2)


class PrimaryCapsule(nn.Module):
    """
    Apply Conv2D with `out_channels` and then reshape to get capsules
    :param in_channels: input channels
    :param out_channels: output channels
    :param dim_caps: dimension of capsule
    :param kernel_size: kernel size
    :return: output tensor, size=[batch, num_caps, dim_caps]
    """
    def __init__(self, in_channels, out_channels, dim_caps, kernel_size, stride=1, padding=0):
        super(PrimaryCapsule, self).__init__()
        self.dim_caps = dim_caps
        self.conv2d = nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size, stride=stride, padding=padding)

    def forward(self, x):
        print(x.shape) #[32, 256, 37, 1]
        outputs = self.conv2d(x)
        outputs = outputs.view(x.size(0), -1, self.dim_caps)
        return squash(outputs)

class CapsuleNet(nn.Module):
    """
    A Capsule Network on MNIST.
    :param input_size: data size = [channels, width, height]
    :param classes: number of classes
    :param routings: number of routing iterations
    Shape:
        - Input: (batch, channels, width, height), optional (batch, classes) .
        - Output:((batch, classes), (batch, channels, width, height))
    """
    def __init__(self, input_size, classes, routings):
        super(CapsuleNet, self).__init__()
        self.input_size = input_size
        self.classes = classes
        self.routings = routings

        # Layer 1: Just a conventional Conv2D layer
        self.conv1 = nn.Conv2d(input_size[0], 256, kernel_size=(4, 200), stride=1, padding=0)

        # Layer 2: Conv2D layer with `squash` activation, then reshape to [None, num_caps, dim_caps]
        self.primarycaps = PrimaryCapsule(256, 256, 8, kernel_size=(37, 1), stride=2, padding=0)

        # Layer 3: Capsule layer. Routing algorithm works here.
        self.digitcaps = DenseCapsule(in_num_caps=32, in_dim_caps=8,
                                      out_num_caps=classes, out_dim_caps=16, routings=routings)

        # Decoder network.
        self.decoder = nn.Sequential(
            nn.Linear(16*classes, 512),
            nn.ReLU(inplace=True),
            nn.Linear(512, 1024),
            nn.ReLU(inplace=True),
            nn.Linear(1024, input_size[0] * input_size[1] * input_size[2]),
            nn.Sigmoid()
        )

        self.relu = nn.ReLU()

    def forward(self, x, y=None):
        x = self.relu(self.conv1(x))
        x = self.primarycaps(x)
        x = self.digitcaps(x)
        length = x.norm(dim=-1)
        if y is None:  # during testing, no label given. create one-hot coding using `length`
            index = length.max(dim=1)[1]
            y = Variable(torch.zeros(length.size()).scatter_(1, index.view(-1, 1).cpu().data, 1.))
        reconstruction = self.decoder((x * y[:, :, None]).view(x.size(0), -1))
        return length, reconstruction.view(-1, *self.input_size)

def caps_loss(y_true, y_pred, x, x_recon, lam_recon):
    """
    Capsule loss = Margin loss + lam_recon * reconstruction loss.
    :param y_true: true labels, one-hot coding, size=[batch, classes]
    :param y_pred: predicted labels by CapsNet, size=[batch, classes]
    :param x: input data, size=[batch, channels, width, height]
    :param x_recon: reconstructed data, size is same as `x`
    :param lam_recon: coefficient for reconstruction loss
    :return: Variable contains a scalar loss value.
    """
    L = y_true * torch.clamp(0.9 - y_pred, min=0.) ** 2 + \
        0.5 * (1 - y_true) * torch.clamp(y_pred - 0.1, min=0.) ** 2
    L_margin = L.sum(dim=1).mean()
    L_recon = nn.MSELoss()(x_recon, x)
    return L_margin + lam_recon * L_recon

def test(model, test_loader, args):
    model.eval()
    test_loss = 0
    correct = 0
    for x, y in test_loader:
        y = torch.zeros(y.size(0), 10).scatter_(1, y.view(-1, 1), 1.)
        x, y = Variable(x.cuda(), volatile=True), Variable(y.cuda())
        y_pred, x_recon = model(x)
        test_loss += caps_loss(y, y_pred, x, x_recon, args.lam_recon).data[0] * x.size(0)  # sum up batch loss
        y_pred = y_pred.data.max(1)[1]
        y_true = y.data.max(1)[1]
        correct += y_pred.eq(y_true).cpu().sum()

    test_loss /= len(test_loader.dataset)
    return test_loss, correct / len(test_loader.dataset)


def train(model, train_loader, test_loader, args):
    """
    Training a CapsuleNet
    :param model: the CapsuleNet model
    :param train_loader: torch.utils.data.DataLoader for training data
    :param test_loader: torch.utils.data.DataLoader for test data
    :param args: arguments
    :return: The trained model
    """
    print('Begin Training' + '-'*70)
    from time import time
    import csv
    logfile = open(args.save_dir + '/log.csv', 'w')
    logwriter = csv.DictWriter(logfile, fieldnames=['epoch', 'loss', 'val_loss', 'val_acc'])
    logwriter.writeheader()

    t0 = time()
    optimizer = Adam(model.parameters(), lr=args.lr)
    lr_decay = lr_scheduler.ExponentialLR(optimizer, gamma=args.lr_decay)
    best_val_acc = 0.
    for epoch in range(args.epochs):
        model.train()  # set to training mode
        lr_decay.step()  # decrease the learning rate by multiplying a factor `gamma`
        ti = time()
        training_loss = 0.0
        for i, (x, y) in enumerate(train_loader):  # batch training
            y = torch.zeros(y.size(0), 10).scatter_(1, y.view(-1, 1), 1.)  # change to one-hot coding
            x, y = Variable(x.cuda()), Variable(y.cuda())  # convert input data to GPU Variable

            optimizer.zero_grad()  # set gradients of optimizer to zero
            y_pred, x_recon = model(x, y)  # forward
            loss = caps_loss(y, y_pred, x, x_recon, args.lam_recon)  # compute loss
            loss.backward()  # backward, compute all gradients of loss w.r.t all Variables
            training_loss += loss.data[0] * x.size(0)  # record the batch loss
            optimizer.step()  # update the trainable parameters with computed gradients

        # compute validation loss and acc
        val_loss, val_acc = test(model, test_loader, args)
        logwriter.writerow(dict(epoch=epoch, loss=training_loss / len(train_loader.dataset),
                                val_loss=val_loss, val_acc=val_acc))
        print("==> Epoch %02d: loss=%.5f, val_loss=%.5f, val_acc=%.4f, time=%ds"
              % (epoch, training_loss / len(train_loader.dataset),
                 val_loss, val_acc, time() - ti))
        if val_acc > best_val_acc:  # update best validation acc and save model
            best_val_acc = val_acc
            torch.save(model.state_dict(), args.save_dir + '/epoch%d.pkl' % epoch)
            print("best val_acc increased to %.4f" % best_val_acc)
    logfile.close()
    torch.save(model.state_dict(), args.save_dir + '/trained_model.pkl')
    print('Trained model saved to \'%s/trained_model.h5\'' % args.save_dir)
    print("Total time = %ds" % (time() - t0))
    print('End Training' + '-' * 70)
    return model

if __name__ == '__main__':
    x = torch.rand([16, 1, 40, 200])
    m = CapsuleNet([1, 40, 200], 203, 3)
    y_pred, x_recon = m(x)
    print(y_pred.shape)

    import argparse
    import os

    # setting the hyper parameters
    parser = argparse.ArgumentParser(description="Capsule Network on MNIST.")
    parser.add_argument('--epochs', default=50, type=int)
    parser.add_argument('--batch_size', default=100, type=int)
    parser.add_argument('--lr', default=0.001, type=float,
                        help="Initial learning rate")
    parser.add_argument('--lr_decay', default=0.9, type=float,
                        help="The value multiplied by lr at each epoch. Set a larger value for larger epochs")
    parser.add_argument('--lam_recon', default=0.0005 * 784, type=float,
                        help="The coefficient for the loss of decoder")
    parser.add_argument('-r', '--routings', default=3, type=int,
                        help="Number of iterations used in routing algorithm. should > 0")  # num_routing should > 0
    parser.add_argument('--shift_pixels', default=2, type=int,
                        help="Number of pixels to shift at most in each direction.")
    parser.add_argument('--data_dir', default='./data',
                        help="Directory of data. If no data, use \'--download\' flag to download it")
    parser.add_argument('--download', action='store_true',
                        help="Download the required data.")
    parser.add_argument('--save_dir', default='./result')
    parser.add_argument('-t', '--testing', action='store_true',
                        help="Test the trained model on testing dataset")
    parser.add_argument('-w', '--weights', default=None,
                        help="The path of the saved weights. Should be specified when testing")
    args = parser.parse_args()
    print(args)
    if not os.path.exists(args.save_dir):
        os.makedirs(args.save_dir)

    # load data
    train_loader, test_loader = load_data(args.data_dir, download=False, batch_size=args.batch_size)

    # define model
    model = CapsuleNet(input_size=[1, 28, 28], classes=10, routings=3)
    print(model)

    # train or test
    if args.weights is not None:  # init the model weights with provided one
        model.load_state_dict(torch.load(args.weights))
    if not args.testing:
        train(model, train_loader, test_loader, args)
    else:  # testing
        if args.weights is None:
            print('No weights are provided. Will test using random initialized weights.')
        test_loss, test_acc = test(model=model, test_loader=test_loader, args=args)
        print('test acc = %.4f, test loss = %.5f' % (test_acc, test_loss))