(七)详解pytorch中的交叉熵损失函数nn.BCELoss()、nn.BCELossWithLogits(),二分类任务如何定义损失函数,如何计算准确率、如何预测
最近在做交叉熵的魔改,所以需要好好了解下交叉熵,遂有此文。
关于交叉熵的定义请自行百度,相信点进来的你对其基本概念不陌生。
本文将结合PyTorch,介绍离散形式的交叉熵在二分类以及多分类中的应用。注意,本文出现的二分类交叉熵和多分类交叉熵,本质上都是一个东西,二分类交叉熵可以看作是多分类交叉熵的一个特例,只不过在PyTorch中对应方法的实现方式不同(不同之处将在正文详细讲解)。
好了,废话少叙,正文开始~
https://zhuanlan.zhihu.com/p/369699003
一、二分类交叉熵
其中,是总样本数,
是第
个样本的所属类别,
是第
个样本的预测值,一般来说,它是一个概率值。
上栗子:
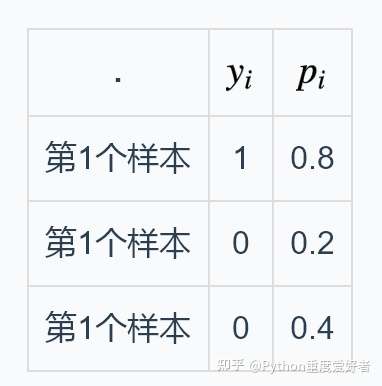
按照上面的公式,交叉熵计算如下:

其实,在PyTorch中已经内置了BCELoss,它的主要用途是计算二分类问题的交叉熵,我们可以调用该方法,并将结果与上面手动计算的结果做个比较:

嗯,结果是一致的。
需要注意的是,输入BCELoss中的预测值应该是个概率。
上面的栗子直接给出了预测的,这是符合要求的。但在更一般的二分类问题中,网络的输出取值是整个实数域(可正可负可为0)。
为了由这种输出值得到对应的,你可以在网络的输出层之后新加一个
Sigmoid层,这样便可以将输出值的取值规范到0和1之间,这就是交叉熵公式中的。
当然,你也可以不更改网络输出,而是在将输出值送入交叉熵公式进行性计算之前,手动用Simgmoid函数做一个映射。
在PyTorch中,甚至提供了BCEWithLogitsLoss方法,它可以直接将输入的值规范到0和1 之间,相当于将Sigmoid和BCELoss集成在了一个方法中。
还是举个栗子来具体进行说明:假设pred是shape为[4,2]的tensor,其中4代表样本个数,2代表该样本分别属于两个类别的概率(前提是规范到了0和1之间,否则就是两个实数域上的值,记住,现在我们讨论的是二分类);target是shape为[4]的tensor,4即样本数。
pred=torch.randn(4,2)#预测值
target=torch.rand(4).random_(0,2)#真实类别标签
在使用任何一种方法之前,都需要先对target做独热编码,否则target和pred维度不匹配:
#将target进行独热编码
onehot_target=torch.eye(2)[target.long(), :]
在做编码前,target看起来长这样:
tensor([0., 1., 1., 1.])
编码后,target变成了这样:
tensor([[1., 0.],
[0., 1.],
[0., 1.],
[0., 1.]])
现在,target的shape也是[4,2]了,和pred的shape一样,所以下面可以开始计算交叉熵了。
- 使用
Sigmoid和BCELoss计算交叉熵
先使用nn.Sigmoid做一下映射:

可以看到,映射后的取值已经被规范到了0和1之间。
然后使用BCELoss进行计算:

- 只使用
BCELossWithLogits计算交叉熵

两种方法的计算结果完全一致。不过官方建议使用BCELossWithLogits,理由是能够提升数值计算稳定性。
以后,当你使用PyTorch内置的二分类交叉熵损失函数时,只要保证输入的预测值和真实标签的维度一致(N,...),且输入的预测值是一个概率即可。满足这两点,一般就能避免常见的错误了。
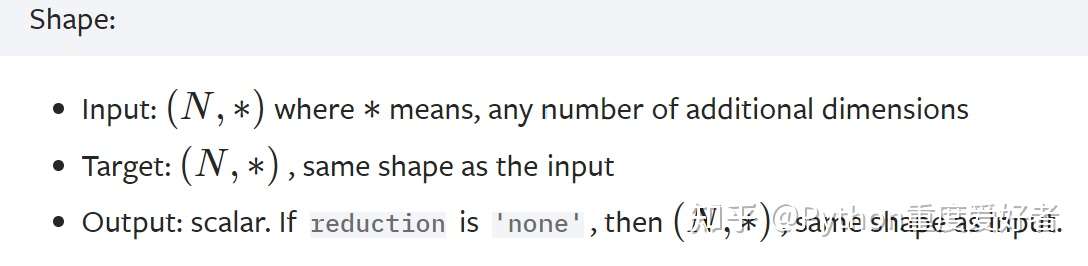
(BCELoss的使用)
关于二分类交叉熵的介绍就到这里,接下来介绍多分类交叉熵。
二、多分类交叉熵
其中,N代表样本数,K代表类别数,代表第i个样本属于类别c的概率,
,
,可以看作一个one-hot编码(若第i个样本属于类别c,则对应位置的
取1,否则取0)。
这个公式乍看上去有点复杂,其实不难。不妨取第个样本,计算这个样本的交叉熵,公式如下:
假设N=2, K=3,即总共3个样本,3个类别,样本的数据如下
|. | |
|
|
|
|
| | :--------: | :--------:| :------: |:------:| | 第1个样本 | 0| 1 |0|0.2|0.3|0.5| | 第2个样本 | 1| 0 |0|0.3|0.2|0.5| | 第3个样本 | 0| 0 |1|0.4|0.4|0.2|
看吧,最终的交叉熵只不过是做了N这样的计算,然后平均一下,加个负号:
你可能已经发现,这里的之和为1。没错,这是网络的输出做了softmax后得到的结果。在上一部分关于二分类的问题中,输入交叉熵公式的网络预测值必须经过
Sigmoid进行映射,而在这里的多分类问题中,需要将Sigmoid替换成Softmax,这是两者的一个重要区别!
现在让我们用代码来实现上面的计算过程:
#预测值,假设已做softmax pred=torch.tensor([[0.2,0.3,0.5],[0.3,0.2,0.5],[0.4,0.4,0.2]]) #真实类别标签 target=torch.tensor([1,0,2]) # 对真实类别标签做 独热编码 one_hot = F.one_hot(target).float() """ one_hot: tensor([[0., 1., 0.], [1., 0., 0.], [0., 0., 1.]]) """ #对预测值取log log=torch.log(pred) #计算最终的结果 res=-torch.sum(one_hot*log)/target.shape[0] print(res)# tensor(1.3391)
这和我们之前手动计算的结果是一样的。代码很简单,只需注意代码中的one_hot*log是逐元素做乘法。
以上是其内部实现原理。在实际使用时,为了方便,PyTorch已经封装好了以上过程,你只需要调用一下相应的方法或函数即可。
在PyTorch中,有一个叫做nll_loss的函数,可以帮助我们更快的实现上述计算,此时无需对target进行独热编码,于是代码可简化如下:
import torch.nn.functional as F #预测值,已做softmax pred=torch.tensor([[0.2,0.3,0.5],[0.3,0.2,0.5],[0.4,0.4,0.2]]) #真实类别标签,此时无需再做one_hot,因为nll_loss会自动做 target=torch.tensor([1,0,2]) #对预测值取log log=torch.log(pred) #计算最终的结果 res=F.nll_loss(log, target) print(res)# tensor(1.3391)
等等,还没完。在PyTorch中,最常用于多分类问题的,是CrossEntropyLoss.
它可以看作是softmax+log+nll_loss的集成。
上面的栗子中的预测值是已经做完softmax之后的,为了说明CrossEntropyLoss的原理,我们换一个预测值没有做过softmax的新栗子,这种栗子也是我们通常会遇到的情况:
#4个样本,3分类 pred=torch.rand(4,3) #真实类别标签 target=torch.tensor([0,1,0,2]) 先按照softmax+log+nll_loss的步骤走一遍: logsoftmax=F.log_softmax(pred) """ logsoftmax: tensor([[-0.8766, -1.4375, -1.0605], [-1.0188, -0.9754, -1.3397], [-0.8926, -1.0962, -1.3615], [-1.0364, -0.8817, -1.4645]]) """ res=F.nll_loss(logsoftmax,target) pritnt(res)#tensor(1.0523) 直接使用CrossEntropyLoss: res=F.cross_entropy(pred, target) print(res)#tensor(1.0523)
结果是一样的。

(CrossEntropyLoss的使用)
三、总结
1、对于二分类任务,网络输出和标签维度:
import torch import torch.nn as nn loss = nn.BCELoss() pre = torch.tensor([0.8, 0.2, 0.6, 0.1]) label = torch.tensor([1., 0., 1., 1.]) print(loss(pre, label)) pre = torch.tensor([[0.2, 0.8], [0.8, 0.2], [0.4, 0.6], [0.9, 0.1]]) label = torch.tensor([[0., 1.], [1., 0.], [0., 1.], [0., 1.]]) print(loss(pre, label)) pre = torch.tensor([[0.8], [0.2], [0.6], [0.1]]) label = torch.tensor([[1.], [0.], [1.], [1.]]) print(loss(pre, label))
输出为:
D:\Users\zxr20\Anaconda3\envs\pt\python.exe F:/semantics/wrapper/test.py tensor(0.8149) tensor(0.8149) tensor(0.8149) Process finished with exit code 0
也就是说,网络输出的维度是一维或者二维都可以, label不用one-hot编码也可以。
前提是,网络输出必须是经过torch.sigmoid函数映射成[0,1]之间的小数。
如前面,一个batch是4, 也就是4个样本。
如果使用第一种方式,计算准确率时候,要这样:
一、第一种方式:
(1)网络输出时候,就要将数值进行sigmoid
(2)损失函数loss = nn.BCELoss()
(3)计算准确率时候如下:
def binary_acc(self, preds, y): preds = torch.round(preds) correct = torch.eq(preds, y).float() acc = correct.sum() / len(correct) return acc
(4)预测时候:
preds = torch.round(preds)
(5)送入critiation
loss = criterion(distence, label.float())
二、第二种方式:
(1)网络输出时候,不用sigmoid
def forward(self, data1, data2): out1, (h1, c1) = self.lstm(data1) out2, (h2, c2) = self.lstm(data2) pre1 = out1[:, -1, :] pre2 = out2[:, -1, :] pre = torch.cat([pre1, pre2], dim=1) out = self.fc(pre) return out
(2)损失函数
self.criterion = nn.BCEWithLogitsLoss().to(self.device)
(3)计算准确率时候如下:
def binary_acc(self, preds, y): preds = torch.round(torch.sigmoid(preds)) correct = torch.eq(preds, y).float() acc = correct.sum() / len(correct) return acc
(4)预测时候
preds = torch.round(torch.sigmoid(preds))


 浙公网安备 33010602011771号
浙公网安备 33010602011771号