(五)对抗训练详解

https://spaces.ac.cn/archives/7234

https://fyubang.com/2019/10/15/adversarial-train/

一、KERAS实现

当前，说到深度学习中的对抗，一般会有两个含义：一个是生成对抗网络（Generative Adversarial Networks，GAN），代表着一大类先进的生成模型；另一个则是跟对抗攻击、对抗样本相关的领域，它跟GAN相关，但又很不一样，它主要关心的是模型在小扰动下的稳健性。本博客里以前所涉及的对抗话题，都是前一种含义，而今天，我们来聊聊后一种含义中的“对抗训练”。

本文包括如下内容：

1、对抗样本、对抗训练等基本概念的介绍；

2、介绍基于快速梯度上升的对抗训练及其在NLP中的应用；

3、给出了对抗训练的Keras实现（一行代码调用）；

4、讨论了对抗训练与梯度惩罚的等价性；

5、基于梯度惩罚，给出了一种对抗训练的直观的几何理解。

方法介绍 #

近年来，随着深度学习的日益发展和落地，对抗样本也得到了越来越多的关注。在CV领域，我们需要通过对模型的对抗攻击和防御来增强模型的稳健型，比如在自动驾驶系统中，要防止模型因为一些随机噪声就将红灯识别为绿灯。在NLP领域，类似的对抗训练也是存在的，不过NLP中的对抗训练更多是作为一种正则化手段来提高模型的泛化能力！

这使得对抗训练成为了NLP刷榜的“神器”之一，前有微软通过RoBERTa+对抗训练在GLUE上超过了原生RoBERTa，后有我司的同事通过对抗训练刷新了CoQA榜单。这也成功引起了笔者对它的兴趣，遂学习了一番，分享在此。

基本概念 #

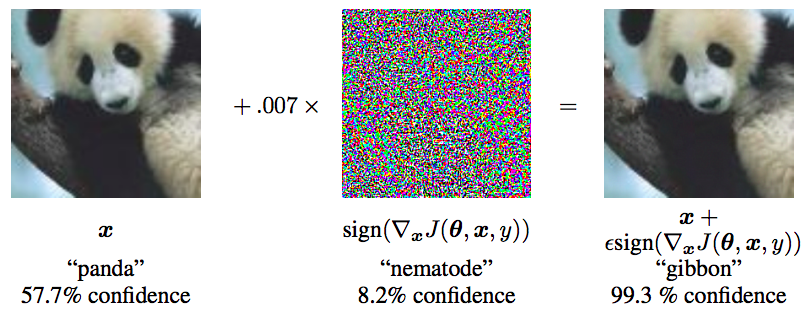
要认识对抗训练，首先要了解“对抗样本”，它首先出现在论文《Intriguing properties of neural networks》之中。简单来说，它是指对于人类来说“看起来”几乎一样、但对于模型来说预测结果却完全不一样的样本，比如下面的经典例子：

对抗样本经典例子。来自论文《Explaining and Harnessing Adversarial Examples》

理解对抗样本之后，也就不难理解各种相关概念了，比如“对抗攻击”，其实就是想办法造出更多的对抗样本，而“对抗防御”，就是想办法让模型能正确识别更多的对抗样本。所谓对抗训练，则是属于对抗防御的一种，它构造了一些对抗样本加入到原数据集中，希望增强模型对对抗样本的鲁棒性；同时，如本文开篇所提到的，在NLP中它通常还能提高模型的表现。

Min-Max #

总的来说，对抗训练可以统一写成如下格式

min θ E (x, y) \sim D [max Δ x \in Ω L (x + Δ x, y; θ)]

其中 $D$

这个式子可以分步理解如下：

1、往属于 $x$

2、当然 $Δ x$

3、每个样本都构造出对抗样本 $x + Δ x$

4、反复交替执行1、2、3步。

由此观之，整个优化过程是 $max$

快速梯度 #

现在的问题是如何计算 $Δ x$

Δ x = ϵ \nabla x L (x, y; θ) (2)

$D$

Δ x = ϵ \nabla x L ( x , y ; θ ) ∥ \nabla x L ( x , y ; θ ) ∥

$D$

min θ E (x, y) \sim D [L (x + Δ x, y; θ)] (4)

$D$

此外，对抗训练还有一种方法，叫做Projected Gradient Descent（PGD），其实就是通过多迭代几步来达到让 $L (x + Δ x, y; θ)$

回到NLP #

对于CV领域的任务，上述对抗训练的流程可以顺利执行下来，因为图像可以视为普通的连续实数向量， $Δ x$

一个自然的想法是像论文《Adversarial Training Methods for Semi-Supervised Text Classification》一样，将扰动加到Embedding层。这个思路在操作上没有问题，但问题是，扰动后的Embedding向量不一定能匹配上原来的Embedding向量表，这样一来对Embedding层的扰动就无法对应上真实的文本输入，这就不是真正意义上的对抗样本了，因为对抗样本依然能对应一个合理的原始输入。

那么，在Embedding层做对抗扰动还有没有意义呢？有！实验结果显示，在很多任务中，在Embedding层进行对抗扰动能有效提高模型的性能。

实验结果 #

既然有效，那我们肯定就要亲自做实验验证一下了。怎么通过代码实现对抗训练呢？怎么才能做到用起来尽可能简单呢？最后用起来的效果如何呢？

思路分析 #

对于CV任务来说，一般输入张量的shape是 $(b, h, w, c)$

对于NLP任务来说，原则上也要对Embedding层的输出进行同样的操作，Embedding层的输出shape为 $(b, n, d)$

不过，我们可以退而求其次。Embedding层的输出是直接取自于Embedding参数矩阵的，因此我们可以直接对Embedding参数矩阵进行扰动。这样得到的对抗样本的多样性会少一些（因为不同样本的同一个token共用了相同的扰动），但仍然能起到正则化的作用，而且这样实现起来容易得多。

代码参考 #

基于上述思路，这里给出Keras下基于FGM方式对Embedding层进行对抗训练的参考实现：

https://github.com/bojone/keras_adversarial_training

核心代码如下：

def adversarial_training(model, embedding_name, epsilon=1):
    """给模型添加对抗训练
    其中model是需要添加对抗训练的keras模型，embedding_name
    则是model里边Embedding层的名字。要在模型compile之后使用。
    """
    if model.train_function is None:  # 如果还没有训练函数
        model._make_train_function()  # 手动make
    old_train_function = model.train_function  # 备份旧的训练函数

    # 查找Embedding层
    for output in model.outputs:
        embedding_layer = search_layer(output, embedding_name)
        if embedding_layer is not None:
            break
    if embedding_layer is None:
        raise Exception('Embedding layer not found')

    # 求Embedding梯度
    embeddings = embedding_layer.embeddings  # Embedding矩阵
    gradients = K.gradients(model.total_loss, [embeddings])  # Embedding梯度
    gradients = K.zeros_like(embeddings) + gradients[0]  # 转为dense tensor

    # 封装为函数
    inputs = (model._feed_inputs +
              model._feed_targets +
              model._feed_sample_weights)  # 所有输入层
    embedding_gradients = K.function(
        inputs=inputs,
        outputs=[gradients],
        name='embedding_gradients',
    )  # 封装为函数

    def train_function(inputs):  # 重新定义训练函数
        grads = embedding_gradients(inputs)[0]  # Embedding梯度
        delta = epsilon * grads / (np.sqrt((grads**2).sum()) + 1e-8)  # 计算扰动
        K.set_value(embeddings, K.eval(embeddings) + delta)  # 注入扰动
        outputs = old_train_function(inputs)  # 梯度下降
        K.set_value(embeddings, K.eval(embeddings) - delta)  # 删除扰动
        return outputs

    model.train_function = train_function  # 覆盖原训练函数

定义好上述函数后，给Keras模型增加对抗训练就只需要一行代码了：

# 写好函数后，启用对抗训练只需要一行代码
adversarial_training(model, 'Embedding-Token', 0.5)

需要指出的是，由于每一步算对抗扰动也需要计算梯度，因此每一步训练一共算了两次梯度，因此每步的训练时间会翻倍。

效果比较 #

为了测试实际效果，笔者选了中文CLUE榜的两个分类任务：IFLYTEK和TNEWS，模型选择了中文BERT base。在CLUE榜单上，BERT base模型在这两个数据上的成绩分别是60.29%和56.58%，经过对抗训练后，成绩为62.46%、57.66%，分别提升了2%和1%！

无对抗训练 加对抗训练 IFLYTEK 60.29 % 62.46 % TNEWS 56.58 % 57.66 %

训练脚本请参考：task_iflytek_adversarial_training.py。

当然，同所有正则化手段一样，对抗训练也不能保证每一个任务都能有提升，但从目前大多数“战果”来看，它是一种非常值得尝试的技术手段。此外，BERT的finetune本身就是一个非常玄乎（靠人品）的过程，前些时间论文《Fine-Tuning Pretrained Language Models: Weight Initializations, Data Orders, and Early Stopping》换用不同的随机种子跑了数百次finetune实验，发现最好的结果能高出好几个点，所以如果你跑了一次发现没提升，不妨多跑几次再下结论。

延伸思考 #

在这一节中，我们从另一个视角对上述结果进行分析，从而推出对抗训练的另一种方法，并且得到一种关于对抗训练的更直观的几何理解。

梯度惩罚 #

假设已经得到对抗扰动 $Δ x$

$D$

\nabla θ L (x, y; θ) + ⟨ \nabla θ \nabla x L (x, y; θ), Δ x ⟩ (6)

$D$

1 2 ϵ ∥ \nabla x L ( x , y ; θ ) ∥ 2 (8)

$D$

事实上，这个结果不是新的，据笔者所知，它首先出现论文《Improving the Adversarial Robustness and Interpretability of Deep Neural Networks by Regularizing their Input Gradients》里。只不过这篇文章不容易搜到，因为你一旦搜索“adversarial training gradient penalty”等关键词，出来的结果几乎都是WGAN-GP相关的东西。

几何图像 #

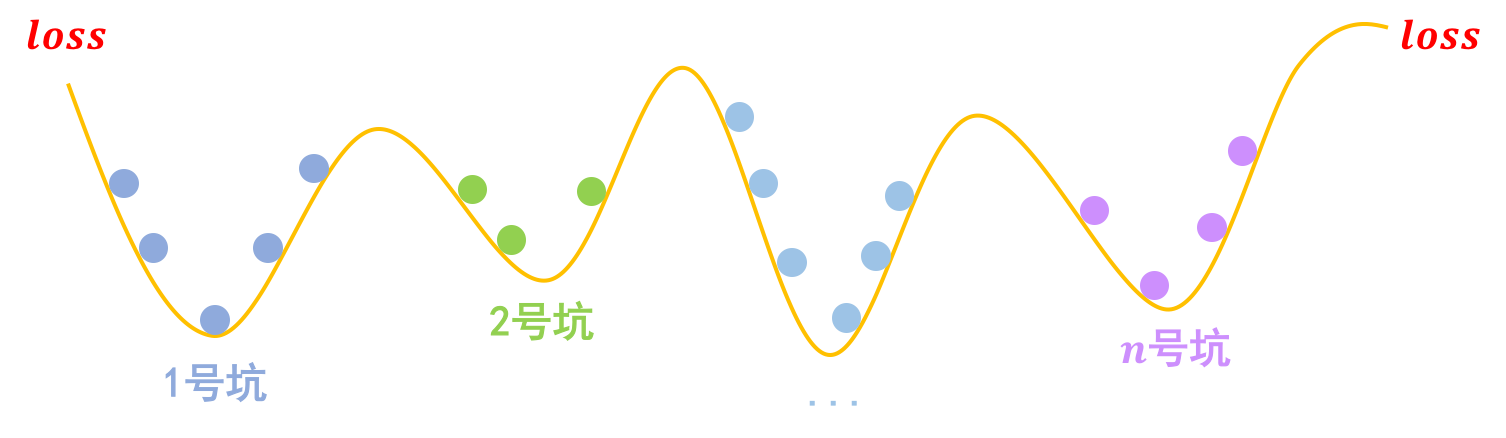
事实上，关于梯度惩罚，我们有一个非常直观的几何图像。以常规的分类问题为例，假设有 $n$

分类问题就是挖坑，然后将同类样本放在同一个坑内

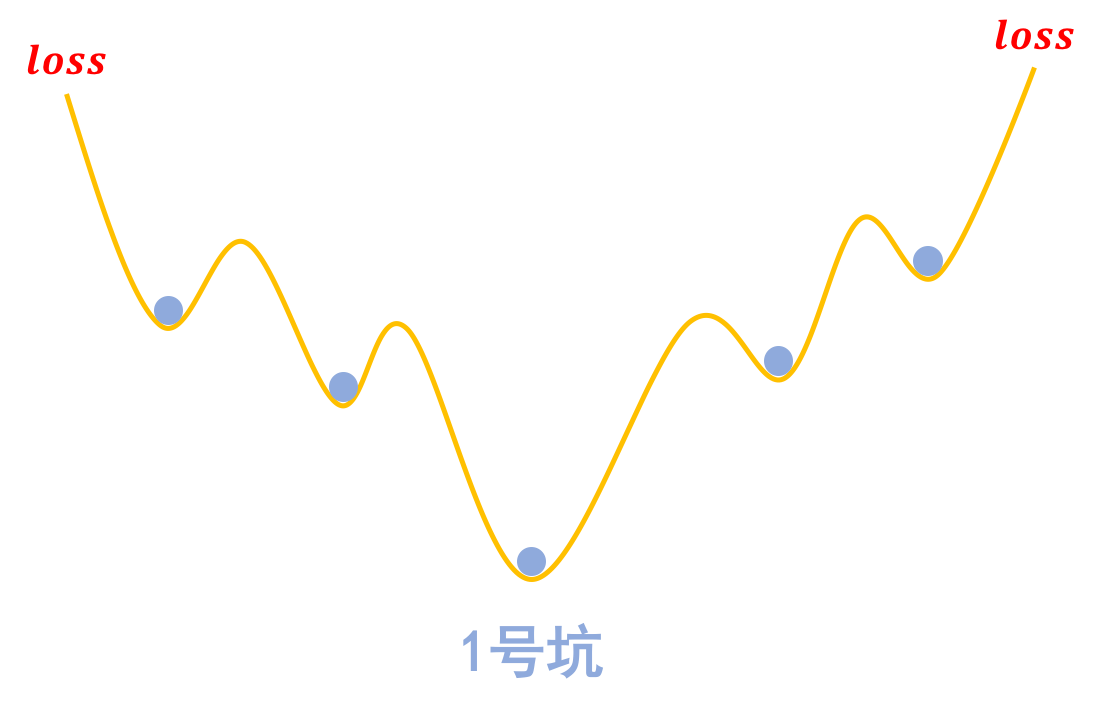
梯度惩罚则说“同类样本不仅要放在同一个坑内，还要放在坑底”，这就要求每个坑的内部要长这样：

对抗训练希望每个样本都在一个“坑中坑”的坑底

为什么要在坑底呢？因为物理学告诉我们，坑底最稳定呀，所以就越不容易受干扰呀，这不就是对抗训练的目的么？

“坑底”最稳定。受到干扰后依然在坑底附近徘徊，不容易挑出坑（跳出坑往往意味着分类错误）

那坑底意味着什么呢？极小值点呀，导数（梯度）为零呀，所以不就是希望 $‖ \nabla_{x} L (x, y; θ) ‖$

L约束 #

我们还可以从L约束（Lipschitz约束）的角度来看梯度惩罚。所谓对抗样本，就是输入的小扰动导致输出的大变化，而关于输入输出的控制问题，我们之前在文章《深度学习中的L约束：泛化与生成模型》就已经探讨过。一个好的模型，理论上应该是“输入的小扰动导致导致输出的小变化”，而为了做到这一点，一个很常用的方案是让模型满足L约束，即存在常数 $L$

∥ f (x 1) - f (x 2) ∥ \leq L ∥ x 1 - x 2 ∥ (9)

$D$

美中不足的是，谱归一化是对模型的每一层权重都进行这样的操作，结果就是神经网络的每一层都满足L约束，这是不必要的（我们只希望整个模型满足L约束，不必强求每一层都满足），因此理论上来说L约束会降低模型表达能力，从而降低模型性能。而在WGAN系列模型中，为了让判别器满足L约束，除了谱归一化外，还有一种常见的方案，那就是梯度惩罚。因此，梯度惩罚也可以理解为一个促使模型满足L约束的正则项，而满足L约束则能有效地抵御对抗样本的攻击。

代码实现 #

既然梯度惩罚号称能有类似的效果，那必然也是要接受实验验证的了。相比前面的FGM式对抗训练，其实梯度惩罚实现起来还容易一些，因为它就是在loss里边多加一项罢了，而且实现方式是通用的，不用区分CV还是NLP。

Keras参考实现如下：

def sparse_categorical_crossentropy(y_true, y_pred):
    """自定义稀疏交叉熵
    这主要是因为keras自带的sparse_categorical_crossentropy不支持求二阶梯度。
    """
    y_true = K.reshape(y_true, K.shape(y_pred)[:-1])
    y_true = K.cast(y_true, 'int32')
    y_true = K.one_hot(y_true, K.shape(y_pred)[-1])
    return K.categorical_crossentropy(y_true, y_pred)


def loss_with_gradient_penalty(y_true, y_pred, epsilon=1):
    """带梯度惩罚的loss
    """
    loss = K.mean(sparse_categorical_crossentropy(y_true, y_pred))
    embeddings = search_layer(y_pred, 'Embedding-Token').embeddings
    gp = K.sum(K.gradients(loss, [embeddings])[0].values**2)
    return loss + 0.5 * epsilon * gp


model.compile(
    loss=loss_with_gradient_penalty,
    optimizer=Adam(2e-5),
    metrics=['sparse_categorical_accuracy'],
)

可以看到，定义带梯度惩罚的loss非常简单，就两行代码而已。需要指出的是，梯度惩罚意味着参数更新的时候需要算二阶导数，但是Tensorflow和Keras自带的loss函数不一定支持算二阶导数，比如K.categorical_crossentropy支持而K.sparse_categorical_crossentropy不支持，遇到这种情况时，需要自定重新定义loss。

效果比较 #

还是前面两个任务，结果如下表。可以看到，梯度惩罚能取得跟FGM基本一致的结果。

无对抗训练 加对抗训练 加梯度惩罚 IFLYTEK 60.29 % 62.46 % 62.31 % TNEWS 56.58 % 57.66 % 57.81 %

完整的代码请参考：task_iflytek_gradient_penalty.py。

本文小结 #

本文简单介绍了对抗训练的基本概念和推导，着重讲了其中的FGM方法并给出了Keras实现，实验证明它能提高一些NLP模型的泛化性能。此外，本文还讨论了对抗学习与梯度惩罚的联系，并给出了梯度惩罚的一种直观的几何理解。

二、pytorch实现

最近，微软的FreeLB-Roberta [1] 靠着对抗训练 (Adversarial Training) 在GLUE榜上超越了Facebook原生的Roberta，追一科技也用到了这个方法仅凭单模型 [2] 就在CoQA榜单中超过了人类，似乎“对抗训练”一下子变成了NLP任务的一把利器。刚好笔者最近也在看这方面的内容，所以开一篇博客，讲一下。

GLUE Leaderboard

CoQA Leaderboard

提到“对抗”，相信大多数人的第一反应都是CV中的对抗生成网络 (GAN)，殊不知，其实对抗也可以作为一种防御机制，并且经过简单的修改，便能用在NLP任务上，提高模型的泛化能力。关键是，对抗训练可以写成一个插件的形式，用几行代码就可以在训练中自由地调用，简单有效，使用成本低。不过网上的大多数博客对于NLP中的对抗训练都介绍得比较零散且无代码实现，笔者在这篇博客中，对NLP任务中的对抗训练做了一个简单的综述，并提供了插件形式的PyTorch实现。

本文专注于NLP对抗训练的介绍，对对抗攻击基础感兴趣的读者，可以看这几篇博客及论文 [3] [4] [5]，这里就不赘述了。不想要理解理论细节的读者也可以直接看最后的代码实现。

对抗样本

我们常常会听到“对抗样本”、“对抗攻击”、“对抗训练”等等这些令人头秃的概念，为了让大家对“对抗”有个更清晰的认识，我们先把这些概念捋捋清楚。

Taxonomy of Adversarial

Szegedy在14年的ICLR中 [6] 提出了对抗样本这个概念。如上图，对抗样本可以用来攻击和防御，而对抗训练其实是“对抗”家族中防御的一种方式，其基本的原理呢，就是通过添加扰动构造一些对抗样本，放给模型去训练，以攻为守，提高模型在遇到对抗样本时的鲁棒性，同时一定程度也能提高模型的表现和泛化能力。

那么，什么样的样本才是好的对抗样本呢？对抗样本一般需要具有两个特点：

相对于原始输入，所添加的扰动是微小的；
能使模型犯错。

下面是一个对抗样本的例子，决定就是你啦，胖达：

一只胖达加了点扰动就被识别成了长臂猿

对抗训练的基本概念

GAN之父Ian Goodfellow在15年的ICLR中 [7] 第一次提出了对抗训练这个概念，简而言之，就是在原始输入样本 $x$

min θ - log P (y | x + r a d v; θ)

其中， $y$

This linear behavior suggests that cheap, analytical perturbations of a linear model should also damage neural networks.

于是，他提出了 Fast Gradient Sign Method (FGSM) ，来计算输入样本的扰动。扰动可以被定义为：

r a d v = ϵ \cdot sgn (▽ x L (θ, x, y))

其中， $sgn$

在 [7] 中，Goodfellow还总结了对抗训练的两个作用：

提高模型应对恶意对抗样本时的鲁棒性；
作为一种regularization，减少overfitting，提高泛化能力。

Min-Max 公式

在 [7] 中，对抗训练的理论部分被阐述得还是比较intuitive，Madry在2018年的ICLR中 [8]总结了之前的工作，并从优化的视角，将问题重新定义成了一个找鞍点的问题，也就是大名鼎鼎的Min-Max公式：

min θ E (x, y) \sim D [max r a d v \in S L (θ, x + r a d v

该公式分为两个部分，一个是内部损失函数的最大化，一个是外部经验风险的最小化。

内部max是为了找到worst-case的扰动，也就是攻击，其中， $L$
外部min是为了基于该攻击方式，找到最鲁棒的模型参数，也就是防御，其中 $D$

Madry认为，这个公式简单清晰地定义了对抗样本攻防“矛与盾”的两个问题：如何构造足够强的对抗样本？以及，如何使模型变得刀枪不入？剩下的，就是如何求解的问题了。

从 CV 到 NLP

以上提到的一些工作都还是停留在CV领域的，那么问题来了，可否将对抗训练迁移到NLP上呢？答案是肯定的，但是，我们得考虑这么几个问题：

首先，CV任务的输入是连续的RGB的值，而NLP问题中，输入是离散的单词序列，一般以one-hot vector的形式呈现，如果直接在raw text上进行扰动，那么扰动的大小和方向可能都没什么意义。Goodfellow在17年的ICLR中 [9] 提出了可以在连续的embedding上做扰动：

Because the set of high-dimensional one-hot vectors does not admit inﬁnitesimal perturbation, we deﬁne the perturbation on continuous word embeddings instead of discrete word inputs.

乍一思考，觉得这个解决方案似乎特别完美。然而，对比图像领域中直接在原始输入加扰动的做法，在embedding上加扰动会带来这么一个问题：这个被构造出来的“对抗样本”并不能map到某个单词，因此，反过来在inference的时候，对手也没有办法通过修改原始输入得到这样的对抗样本。我们在上面提到，对抗训练有两个作用，一是提高模型对恶意攻击的鲁棒性，二是提高模型的泛化能力。在CV任务，根据经验性的结论，对抗训练往往会使得模型在非对抗样本上的表现变差，然而神奇的是，在NLP任务中，模型的泛化能力反而变强了，如[1]中所述：

While adversarial training boosts the robustness, it is widely accepted by computer vision researchers that it is at odds with generalization, with classiﬁcation accuracy on non-corrupted images dropping as much as 10% on CIFAR-10, and 15% on Imagenet (Madry et al., 2018; Xie et al., 2019). Surprisingly, people observe the opposite result for language models (Miyato et al., 2017; Cheng et al., 2019), showing that adversarial training can improve both generalization and robustness.

因此，在NLP任务中，对抗训练的角色不再是为了防御基于梯度的恶意攻击，反而更多的是作为一种regularization，提高模型的泛化能力。

有了这些“思想准备”，我们来看看NLP对抗训练的常用的几个方法和具体实现吧。

NLP中的两种对抗训练 + PyTorch实现

Fast Gradient Method（FGM）

上面我们提到，Goodfellow在15年的ICLR [7] 中提出了Fast Gradient Sign Method（FGSM），随后，在17年的ICLR [9]中，Goodfellow对FGSM中计算扰动的部分做了一点简单的修改。假设输入的文本序列的embedding vectors $[v_{1}, v_{2}, \dots, v_{T}]$

r a d v g = ϵ \cdot g / | | g | | 2 = ▽ x

实际上就是取消了符号函数，用二范式做了一个scale，需要注意的是：这里的norm计算的是，每个样本的输入序列中出现过的词组成的矩阵的梯度norm。原作者提供了一个TensorFlow的实现 [10]，在他的实现中，公式里的 $x$

class FGM():
    def __init__(self, model):
        self.model = model
        self.backup = {}

    def attack(self, epsilon=1., emb_name='emb.'):
        # emb_name这个参数要换成你模型中embedding的参数名
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name:
                self.backup[name] = param.data.clone()
                norm = torch.norm(param.grad)
                if norm != 0:
                    r_at = epsilon * param.grad / norm
                    param.data.add_(r_at)

    def restore(self, emb_name='emb.'):
        # emb_name这个参数要换成你模型中embedding的参数名
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name: 
                assert name in self.backup
                param.data = self.backup[name]
        self.backup = {}

需要使用对抗训练的时候，只需要添加五行代码：

# 初始化
fgm = FGM(model)
for batch_input, batch_label in data:
    # 正常训练
    loss = model(batch_input, batch_label)
    loss.backward() # 反向传播，得到正常的grad
    # 对抗训练
    fgm.attack() # 在embedding上添加对抗扰动
    loss_adv = model(batch_input, batch_label)
    loss_adv.backward() # 反向传播，并在正常的grad基础上，累加对抗训练的梯度
    fgm.restore() # 恢复embedding参数
    # 梯度下降，更新参数
    optimizer.step()
    model.zero_grad()

PyTorch为了节约内存，在backward的时候并不保存中间变量的梯度。因此，如果需要完全照搬原作的实现，需要用register_hook接口[11]将embedding后的中间变量的梯度保存成全局变量，norm后面两维，计算出扰动后，在对抗训练forward时传入扰动，累加到embedding后的中间变量上，得到新的loss，再进行梯度下降。不过这样实现就与我们追求插件式简单好用的初衷相悖，这里就不赘述了，感兴趣的读者可以自行实现。

Projected Gradient Descent（PGD）

内部max的过程，本质上是一个非凹的约束优化问题，FGM解决的思路其实就是梯度上升，那么FGM简单粗暴的“一步到位”，是不是有可能并不能走到约束内的最优点呢？当然是有可能的。于是，一个很intuitive的改进诞生了：Madry在18年的ICLR中[8]，提出了用Projected Gradient Descent（PGD）的方法，简单的说，就是“小步走，多走几步”，如果走出了扰动半径为 $ϵ$

x t + 1 g (x t) = Π x + S (x t + α g (x t)

其中 $S = {r \in R^{d} : | | r | |_{2} \leq ϵ}$

class PGD():
    def __init__(self, model):
        self.model = model
        self.emb_backup = {}
        self.grad_backup = {}

    def attack(self, epsilon=1., alpha=0.3, emb_name='emb.', is_first_attack=False):
        # emb_name这个参数要换成你模型中embedding的参数名
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name:
                if is_first_attack:
                    self.emb_backup[name] = param.data.clone()
                norm = torch.norm(param.grad)
                if norm != 0:
                    r_at = alpha * param.grad / norm
                    param.data.add_(r_at)
                    param.data = self.project(name, param.data, epsilon)

    def restore(self, emb_name='emb.'):
        # emb_name这个参数要换成你模型中embedding的参数名
        for name, param in self.model.named_parameters():
            if param.requires_grad and emb_name in name: 
                assert name in self.emb_backup
                param.data = self.emb_backup[name]
        self.emb_backup = {}
        
    def project(self, param_name, param_data, epsilon):
        r = param_data - self.emb_backup[param_name]
        if torch.norm(r) > epsilon:
            r = epsilon * r / torch.norm(r)
        return self.emb_backup[param_name] + r
        
    def backup_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                self.grad_backup[name] = param.grad.clone()
    
    def restore_grad(self):
        for name, param in self.model.named_parameters():
            if param.requires_grad:
                param.grad = self.grad_backup[name]

使用的时候，要麻烦一点：

pgd = PGD(model)
K = 3
for batch_input, batch_label in data:
    # 正常训练
    loss = model(batch_input, batch_label)
    loss.backward() # 反向传播，得到正常的grad
    pgd.backup_grad()
    # 对抗训练
    for t in range(K):
        pgd.attack(is_first_attack=(t==0)) # 在embedding上添加对抗扰动, first attack时备份param.data
        if t != K-1:
            model.zero_grad()
        else:
            pgd.restore_grad()
        loss_adv = model(batch_input, batch_label)
        loss_adv.backward() # 反向传播，并在正常的grad基础上，累加对抗训练的梯度
    pgd.restore() # 恢复embedding参数
    # 梯度下降，更新参数
    optimizer.step()
    model.zero_grad()

在[8]中，作者将这一类通过一阶梯度得到的对抗样本称之为“一阶对抗”，在实验中，作者发现，经过PGD训练过的模型，对于所有的一阶对抗都能得到一个低且集中的损失值，如下图所示：

样本+随机扰动在两种模型下的loss值

我们可以看到，面对约束空间 $S$

实验对照

为了说明对抗训练的作用，笔者选了四个GLUE中的任务进行了对照试验。实验代码是用的Huggingface的transfomers/examples/run_glue.py [12]，超参都是默认的，对抗训练用的也是相同的超参。

任务	Metrics	BERT-Base	FGM	PGD
MRPC	Accuracy	83.6	86.8	85.8
CoLA	Matthew’s corr	56.0	56.0	56.8
STS-B	Person/Spearman corr.	89.3/88.8	89.3/88.8	89.3/88.9
RTE	Accuracy	64.3	66.8	64.6

我们可以看到，对抗训练还是有效的，在MRPC和RTE任务上甚至可以提高三四个百分点。不过，根据我们使用的经验来看，是否有效有时也取决于数据集。毕竟：

缘，妙不可言~

总结

这篇博客梳理了NLP对抗训练发展的来龙去脉，介绍了对抗训练的数学定义，并对于两种经典的对抗训练方法，提供了插件式的实现，做了简单的实验对照。由于笔者接触对抗训练的时间也并不长，如果文中有理解偏差的地方，希望读者不吝指出。

一个彩蛋：Virtual Adversarial Training

除了监督训练，对抗训练还可以用在半监督任务中，尤其对于NLP任务来说，很多时候输入的无监督文本多的很，但是很难大规模地进行标注，那么就可以参考[13]中提到的Virtual Adversarial Training进行半监督训练。

首先，我们抽取一个随机标准正态扰动（ $d \sim N (0, I) \in R^{d}$

g x' = ▽ x' D K L (p (\cdot | x; θ) | | p (

然后，用得到的梯度，计算对抗扰动，并进行对抗训练：

min θ x * D K L (p (\cdot | x; θ) | | p (\cdot | x *

实现方法跟FGM差不多，这里就不给出了。

Reference

[1]：FreeLB: Enhanced Adversarial Training for Language Understanding. https://arxiv.org/abs/1909.11764
[2]：Technical report on Conversational Question Answering. https://arxiv.org/abs/1909.10772
[3]：EYD与机器学习：对抗攻击基础知识（一）. https://zhuanlan.zhihu.com/p/37260275
[4]：Towards a Robust Deep Neural Network in Text Domain A Survey. https://arxiv.org/abs/1902.07285
[5]：Adversarial Attacks on Deep Learning Models in Natural Language Processing: A Survey. https://arxiv.org/abs/1901.06796
[6]：Intriguing properties of neural networks. https://arxiv.org/abs/1312.6199
[7]：Explaining and Harnessing Adversarial Examples. https://arxiv.org/abs/1412.6572
[8]：Towards Deep Learning Models Resistant to Adversarial Attacks. https://arxiv.org/abs/1706.06083
[9]：Adversarial Training Methods for Semi-Supervised Text Classification. https://arxiv.org/abs/1605.07725
[10]：Adversarial Text Classification原作实现. https://github.com/tensorflow/models/blob/e97e22dfcde0805379ffa25526a53835f887a860/research/adversarial_text/adversarial_losses.py
[11]：register_hook api. https://www.cnblogs.com/SivilTaram/p/pytorch_intermediate_variable_gradient.html
[12]：huggingface的transformers. https://github.com/huggingface/transformers/tree/master/examples
[13]：Distributional Smoothing with Virtual Adversarial Training. https://arxiv.org/abs/1507.00677

posted @ 2021-03-08 11:03 jasonzhangxianrong 阅读(4555) 评论(0) 编辑收藏举报

刷新页面返回顶部

(五)对抗训练详解

一、KERAS实现

方法介绍 #

基本概念 #

Min-Max #

快速梯度 #

回到NLP #

实验结果 #

思路分析 #

代码参考 #

效果比较 #

延伸思考 #

梯度惩罚 #

几何图像 #

L约束 #

代码实现 #

效果比较 #

本文小结 #

二、pytorch实现

对抗样本

对抗训练的基本概念

Min-Max 公式

从 CV 到 NLP

NLP中的两种对抗训练 + PyTorch实现

Fast Gradient Method（FGM）

Projected Gradient Descent（PGD）

实验对照

总结

一个彩蛋：Virtual Adversarial Training

Reference

公告