pytorch（二十四）：卷积神经网络

一、概念

 

 

卷积神经网络主要是由输入层、卷积层、激活函数、池化层、全连接层、损失函数组成，表面看比较复杂，其实质就是特征提取以及决策推断。

要使特征提取尽量准确，就需要将这些网络层结构进行组合，比如经典的卷积神经网络模型AlexNet:5个卷积层+3个池化层+3个连接层结构。

2.1 卷积（convolution）

卷积的作用就是提取特征，因为一次卷积可能提取的特征比较粗糙，所以多次卷积，以及层层纵深卷积，层层提取特征（千万要区别于多次卷积，因为每一层里含有多次卷积）。

这里可能就有小伙伴问：为什么要进行层层纵深卷积，而且还要每层多次？

你可以理解为物质A有自己的多个特征（高、矮、胖、瘦、、、），所以在物质A上需要多次提取，得到不同的特征，然后这些特征组合后发生化学反应生成物质B，

而物质B又有一些新的专属于自己的特征，所以需要进一步卷积。这是我个人的理解，不对的话或者有更形象的比喻还请不吝赐教啊。

 

在卷积层中，每一层的卷积核是不一样的。比如AlexNet

第一层：96*11*11（96表示卷积核个数，11表示卷积核矩阵宽*高） stride（步长） = 4  pad（边界补零） = 0

第二层：256*5*5 stride（步长） = 1  pad（边界补零） = 2

第三，四层：384*3*3 stride（步长） = 1  pad（边界补零） = 1

第五层：256*3*3 stride（步长） = 1  pad（边界补零） = 2

卷积的篇幅说了这么多，那么到底是如何进行运算的呢，虽说网络上关于卷积运算原理铺天盖地，但是个人总感觉讲得不够透彻，或者说本人智商有待提高，

希望通过如下这幅图（某位大神的杰作）来使各位看官们能够真正理解。

 

 

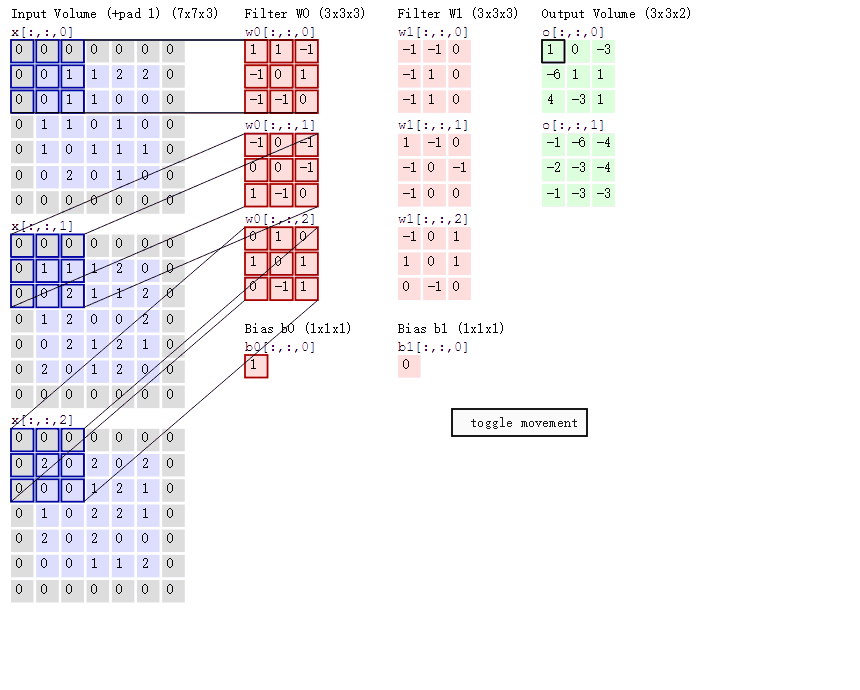
这里举的例子是一个输入图片（5*5*3），卷积核（3*3*3），有两个（Filter W0，W1），偏置b也有两个（Bios b0，b1），卷积结果Output Volumn（3*3*2），步长stride = 2。

输入：7*7*3 是因为 pad = 1 （在图片边界行和列都补零，补零的行和的数目是1），

（对于彩色图片，一般都是RGB3种颜色，号称3通道，7*7指图片高h * 宽w）

，补零的作用是能够提取图片边界的特征。

卷积核深度为什么要设置成3呢？这是因为输入是3通道，所以卷积核深度必须与输入的深度相同。至于卷积核宽w，高h则是可以变化的，但是宽高必须相等。

卷积核输出o[0,0,0] = 3 （Output Volumn下浅绿色框结果），这个结果是如何得到的呢？ 其实关键就是矩阵对应位置相乘再相加（千万不要跟矩阵乘法搞混淆啦）

=> w0[:,:,0] * x[:,:,0]蓝色区域矩阵(R通道) +  w0[:,:,1] * x[:,:,1]蓝色区域矩阵（G通道）+  w0[:,:,2] * x[:,:,2]蓝色区域矩阵（B通道） + b0（千万不能丢，因为 y = w * x + b）

第一项  => 0 * 1 + 0 * 1 + 0 * 1 + 0 * (-1) + 1 * (-1) + 1 * 0 + 0 * (-1) + 1 * 1 + 1 * 0  =  0

第二项 => 0 * (-1) + 0 * (-1) + 0 * 1 + 0 * (-1) + 0 * 1 + 1 * 0 + 0 * (-1) + 2 * 1 + 2 * 0 = 2

第三项 => 0 * 1 + 0 * 0 + 0 * (-1) + 0 * 0 + 2 * 0 + 2 * 0 + 0 * 1 + 0 * (-1) + 0 * (-1) = 0

卷积核输出o[0,0,0] = > 第一项 + 第二项 + 第三项 + b0 = 0 + 2 + 0 + 1 = 3

o[0,0,1] = -5 又是如何得到的呢？

因为这里的stride = 2 ，所以 输入的窗口就要滑动两个步长，也就是红色框的区域，而运算跟之前是一样的

第一项  => 0 * 1 + 0 * 1 + 0 * 1 + 1 * (-1) + 2 * (-1) + 2 * 0 + 1 * (-1) + 1 * 1 + 2 * 0 = -3

第二项 => 0 * (-1) + 0 * (-1) + 0 * 1 + 1 * (-1) + 2 * 1 + 0 * 0 + 2 * (-1) + 1 * 1 + 1 * 0 = 0

第三项 => 0 * 1 + 0 * 0 + 0 * (-1) + 2 * 0 + 0 * 0 + 1 * 0 + 0 * 1 + 2 * (-1) + 1 * (-1)  = - 3

卷积核输出o[0,0,1] = > 第一项 + 第二项 + 第三项 + b0 = (-3) + 0 + (-3) + 1 = -5

之后以此卷积核窗口大小在输入图片上滑动，卷积求出结果，因为有两个卷积核，所有就有两个输出结果。

这里小伙伴可能有个疑问，输出窗口是如何得到的呢？

这里有一个公式：输出窗口宽 w = (输入窗口宽 w - 卷积核宽 w + 2 * pad)/stride  + 1 ，输出高 h  = 输出窗口宽 w

以上面例子， 输出窗口宽 w = ( 5 - 3 + 2 * 1)/2 + 1 = 3 ，则输出窗口大小为 3 * 3，因为有2个输出，所以是 3*3*2。

2.2 Relu激活函数

相信看过卷积神经网络结构（CNN）的伙伴们都知道，激活函数无处不在，特别是CNN中，在卷积层后，全连接（FC）后都有激活函数Relu的身影，

那么这就自然不得不让我们产生疑问：

问题1、为什么要用激活函数？它的作用是什么？

问题2、在CNN中为什么要用Relu，相比于sigmoid，tanh，它的优势在什么地方？

对于第1个问题：由 y = w * x + b 可知，如果不用激活函数，每个网络层的输出都是一种线性输出，而我们所处的现实场景，其实更多的是各种非线性的分布。

这也说明了激活函数的作用是将线性分布转化为非线性分布，能更逼近我们的真实场景。

对于第2个问题： 先看sigmoid，tanh分布

他们在 x -> 时，输出就变成了恒定值，因为求梯度时需要对函数求一阶偏导数，而不论是sigmoid，还是tanhx，他们的偏导都为0，

也就是存在所谓的梯度消失问题，最终也就会导致权重参数w ， b 无法更新。相比之下，Relu就不存在这样的问题，另外在 x > 0 时，

Relu求导 = 1，这对于反向传播计算dw，db，是能够大大的简化运算的。

使用sigmoid还会存在梯度爆炸的问题，比如在进行前向传播和反向传播迭代次数非常多的情况下，sigmoid因为是指数函数，其结果中

某些值会在迭代中累积，并成指数级增长，最终会出现NaN而导致溢出。

2.3 池化

池化层一般在卷积层+ Relu之后，它的作用是：

1、减小输入矩阵的大小（只是宽和高，而不是深度），提取主要特征。（不可否认的是，在池化后，特征会有一定的损失，所以，有些经典模型就去掉了池化这一层）。

它的目的是显而易见的，就是在后续操作时能降低运算。

2、一般采用mean_pooling（均值池化）和max_pooling（最大值池化），对于输入矩阵有translation（平移），rotation（旋转），能够保证特征的不变性。

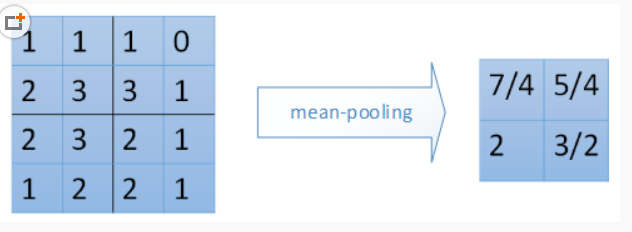
mean_pooling 就是输入矩阵池化区域求均值，这里要注意的是池化窗口在输入矩阵滑动的步长跟stride有关，一般stride = 2.（图片是直接盗过来，这里感谢原创）

最右边7/4 => (1 + 1 + 2 + 3)/4

 

 

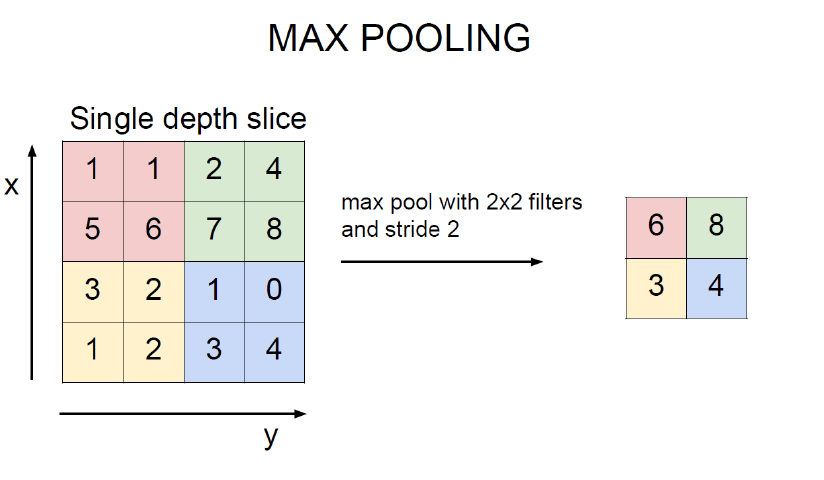
max_pooling 最大值池化，就是每个池化区域的最大值放在输出对应位置上。

2.4 全连接（full connection）

作用：分类器角色，将特征映射到样本标记空间，本质是矩阵变换（affine）。

至于变换的实现见后面的代码流程图，或者最好是跟一下代码，这样理解更透彻。

2.5 损失函数（softmax_loss）

作用：计算损失loss，从而求出梯度grad。

常用损失函数有:MSE均方误差，SVM（支持向量机）合页损失函数，Cross Entropy交叉熵损失函数。

这几种损失函数目前还看不出谁优谁劣，估计只有在具体的应用场景中去验证了。至于这几种损失函数的介绍，

大家可以去参考《常用损失函数小结》https://blog.csdn.net/zhangjunp3/article/details/80467350，这个哥们写得比较详细。

在后面的代码实例中，用到的是softmax_loss，它属于Cross Entropy交叉熵损失函数。

softmax计算公式：

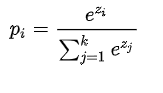
其中， 是要计算的类别  的网络输出，分母是网络输出所有类别之和（共有  个类别）， 表示第  类的概率。

交叉熵损失：

 

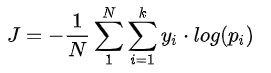
其中， 是类别  的真实标签， 表示第  类的概率， 是样本总数， 是类别数。

梯度:

     =        当   != 

     =    - 1   当   = 

其中  表示真实标签对应索引下预测的目标值， 类别索引。

这个有点折磨人，原理讲解以及推导请大家可以参考这位大神的博客：http://www.cnblogs.com/zongfa/p/8971213.html。

2.6 前向传播（forward propagation）

前向传播包含之前的卷积，Relu激活函数，池化（pool），全连接(fc)，可以说，在损失函数之前操作都属于前向传播。

主要是权重参数w , b 初始化，迭代，以及更新w, b,生成分类器模型。

2.7 反向传播（back propagation）

反向传播包含损失函数，通过梯度计算dw，db，Relu激活函数逆变换，反池化，反全连接。

2.8 随机梯度下降（sgd_momentum）

作用：由梯度grad计算新的权重矩阵w

sgd公式：

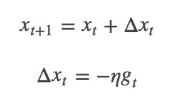
其中，η为学习率，g_t为x在t时刻的梯度。 

一般我们是将整个数据集分成n个epoch，每个epoch再分成m个batch，每次更新都利用一个batch的数据，而非整个训练集。

优点：batch的方法可以减少机器的压力，并且可以更快地收敛。

缺点：其更新方向完全依赖于当前的batch，因而其更新十分不稳定。

为了解决这个问题，momentum就横空出世了，具体原理详解见下路派出所（这名字霸气）的博客http://www.cnblogs.com/callyblog/p/8299074.html。

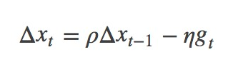
momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。

这样一来，可以在一定程度上增加稳定性，从而学习地更快，并且还有一定摆脱局部最优的能力：

其中，ρ 即momentum，表示要在多大程度上保留原来的更新方向，这个值在0-1之间，在训练开始时，由于梯度可能会很大，所以初始值一般选为0.5；

当梯度不那么大时，改为0.9。η 是学习率，即当前batch的梯度多大程度上影响最终更新方向，跟普通的SGD含义相同。ρ 与 η 之和不一定为1。

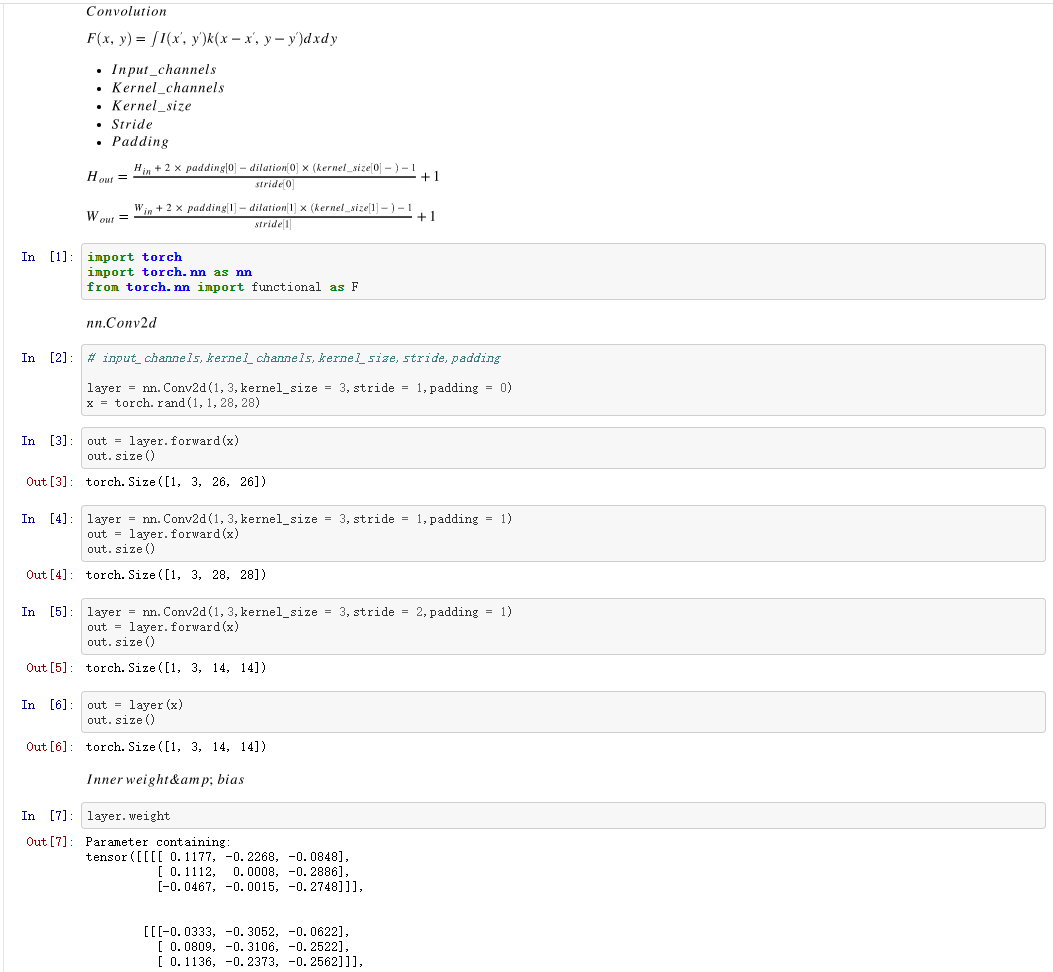
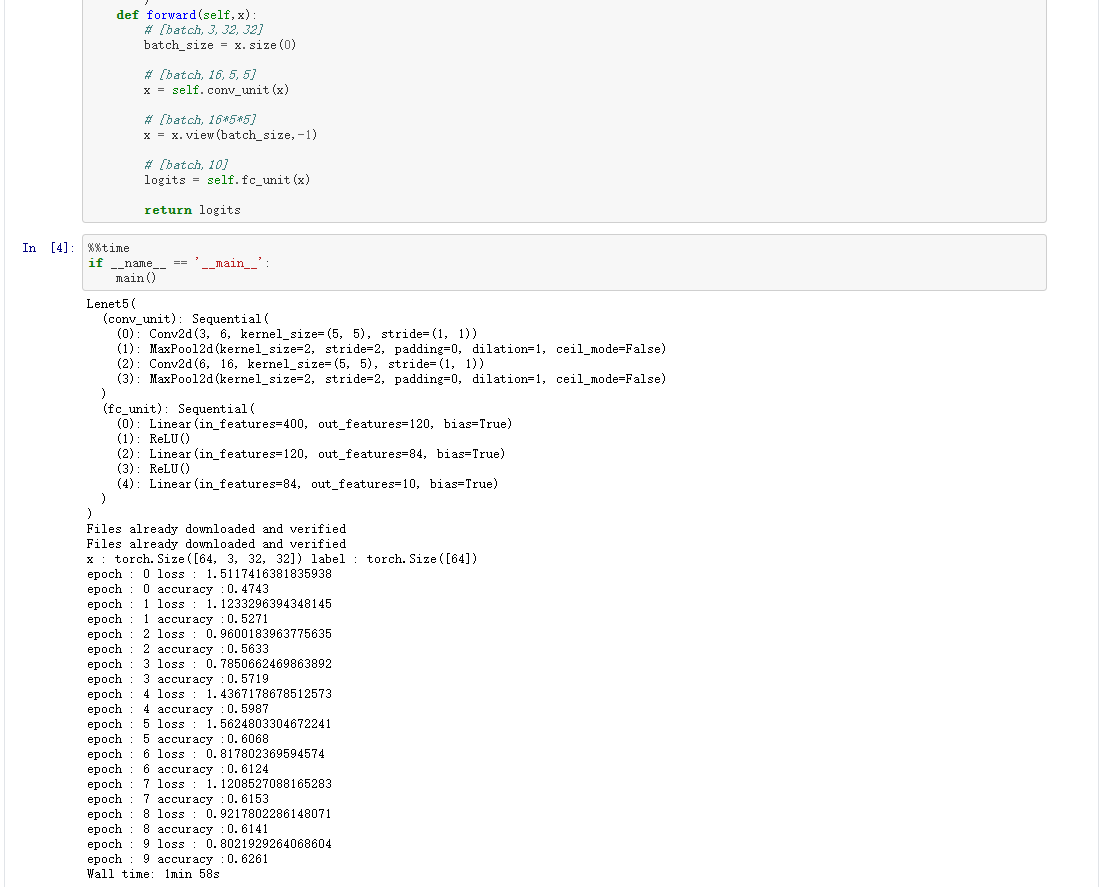
二、pytorch实现

 

 

 

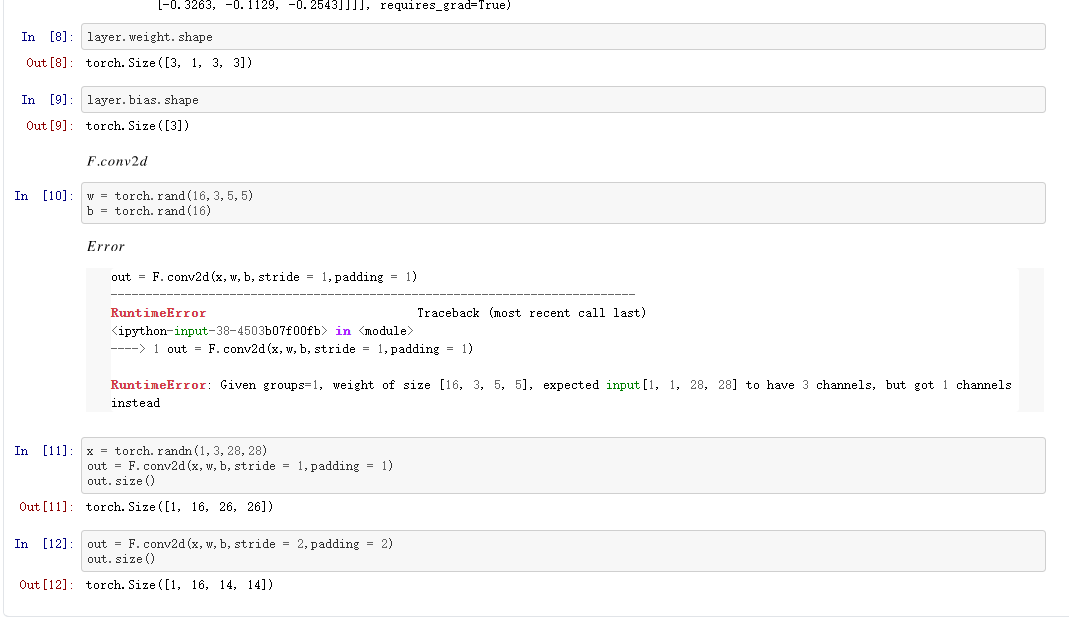
 三、Pooling-Sampling

 

 

 

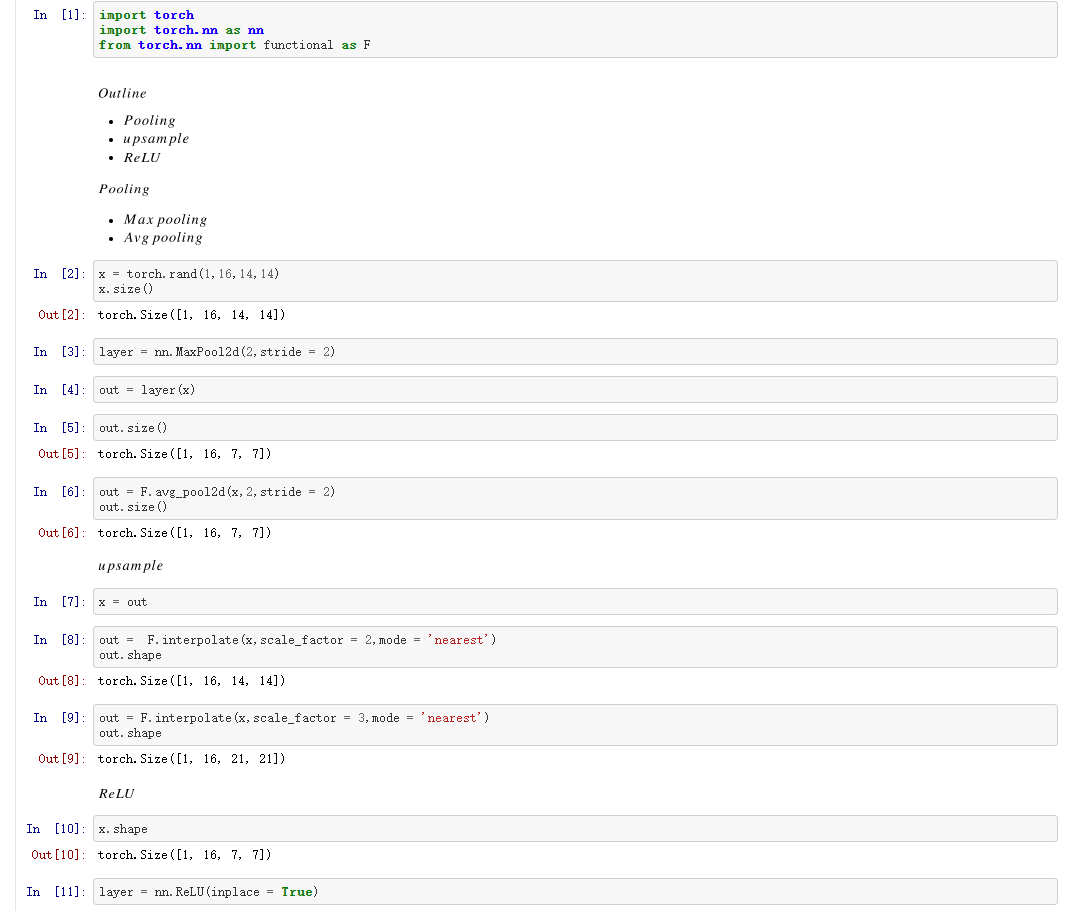
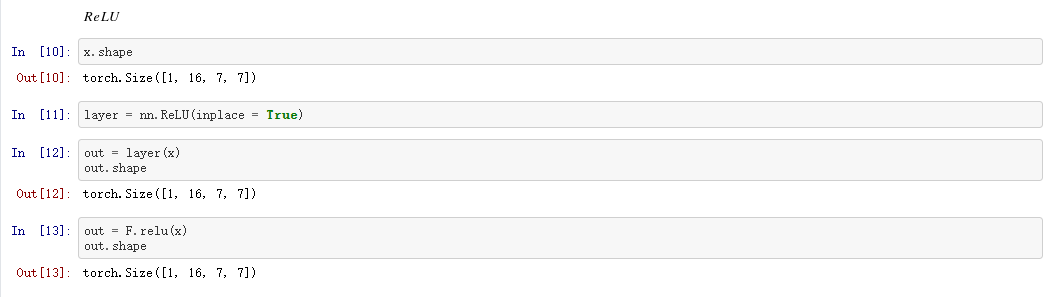
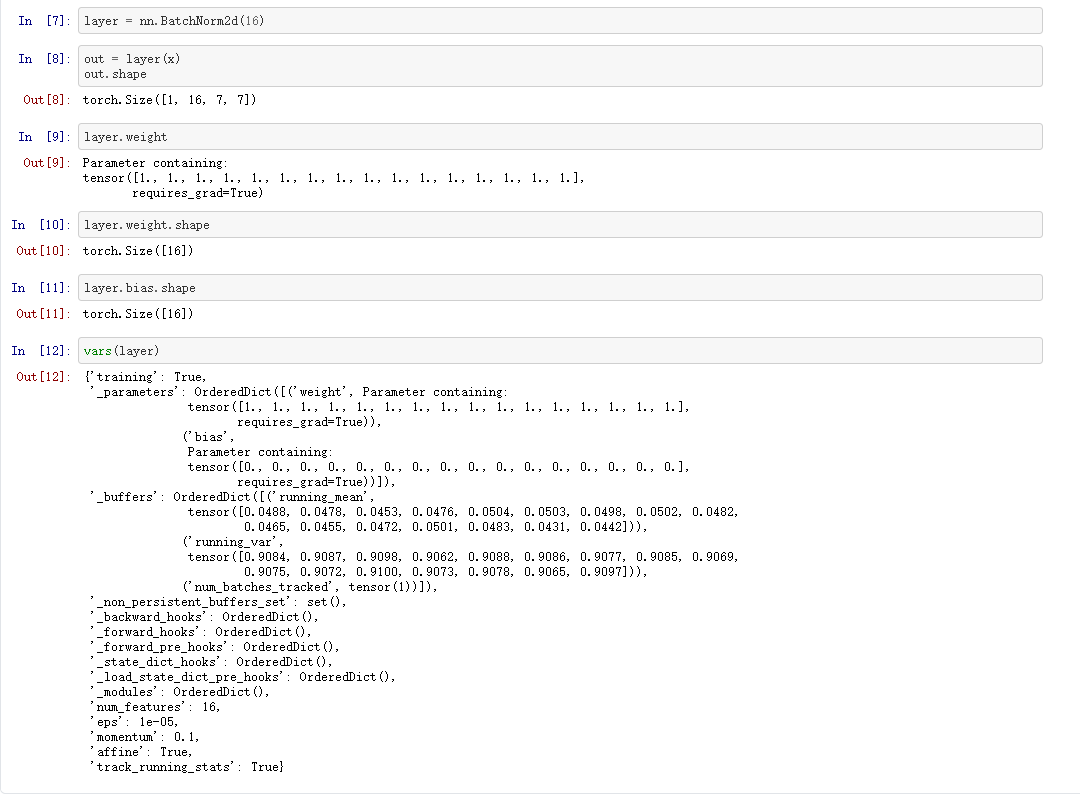
 四、BatchNorm

 

 

 

 

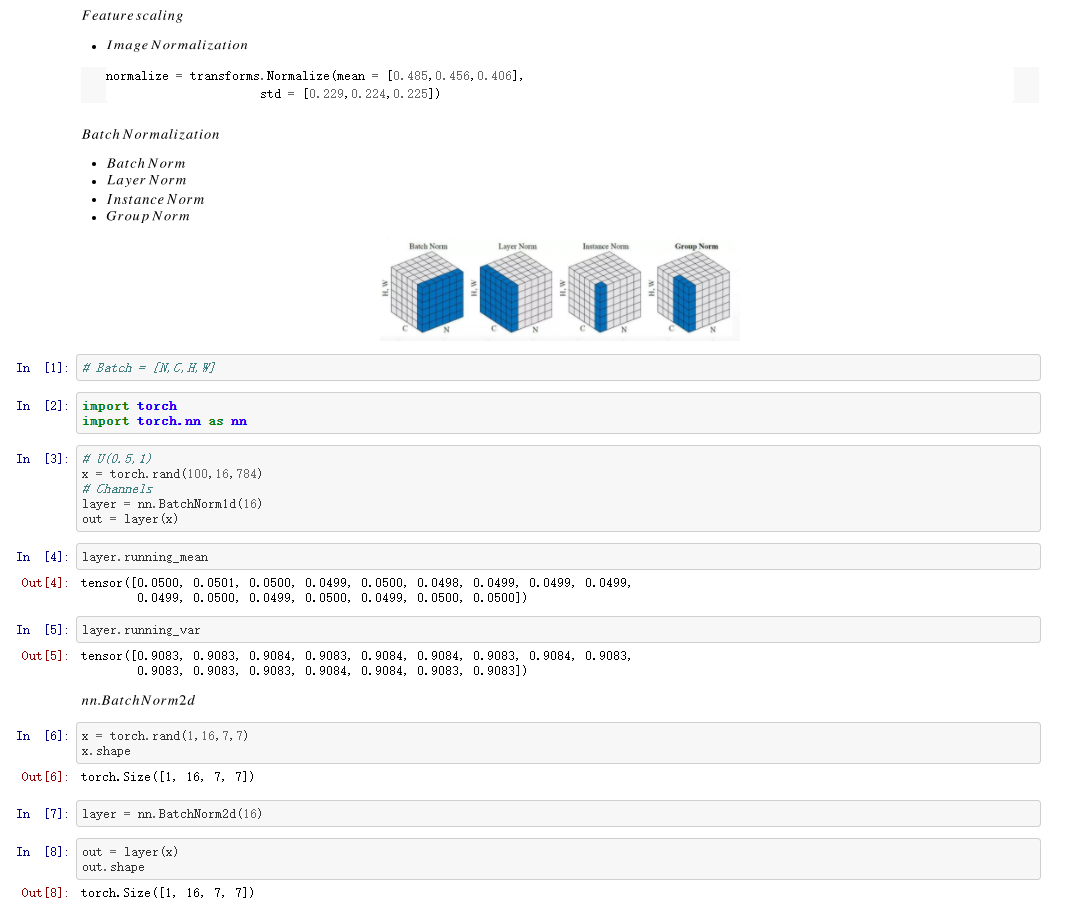
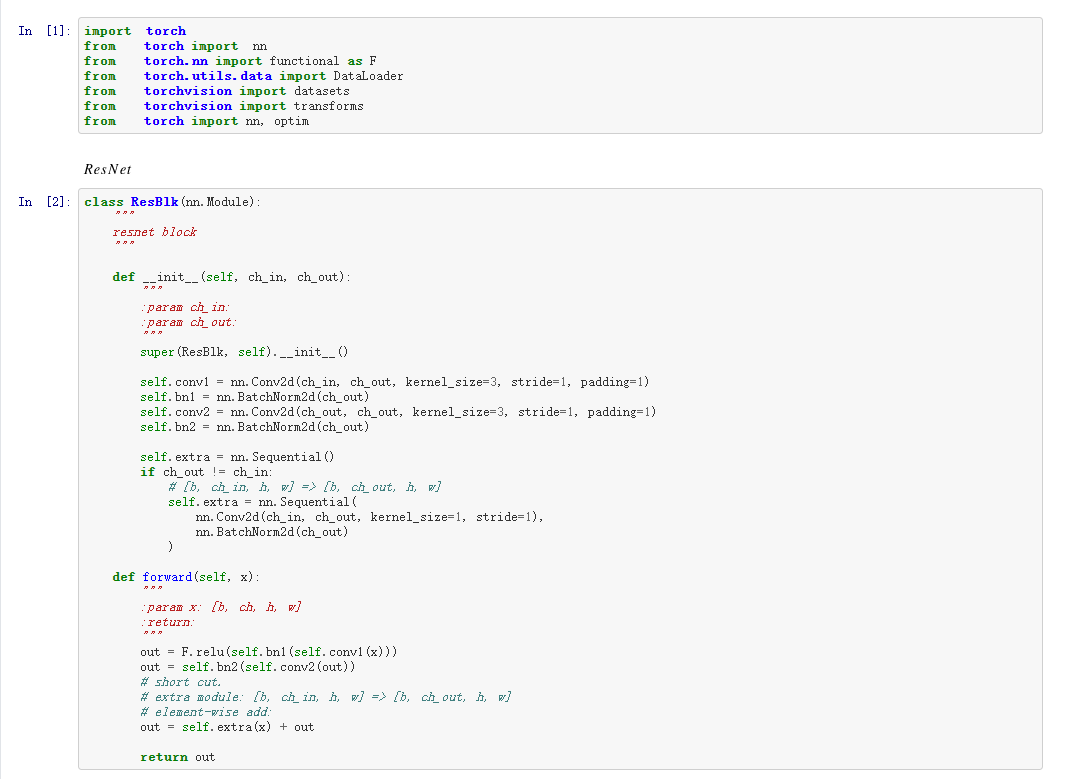
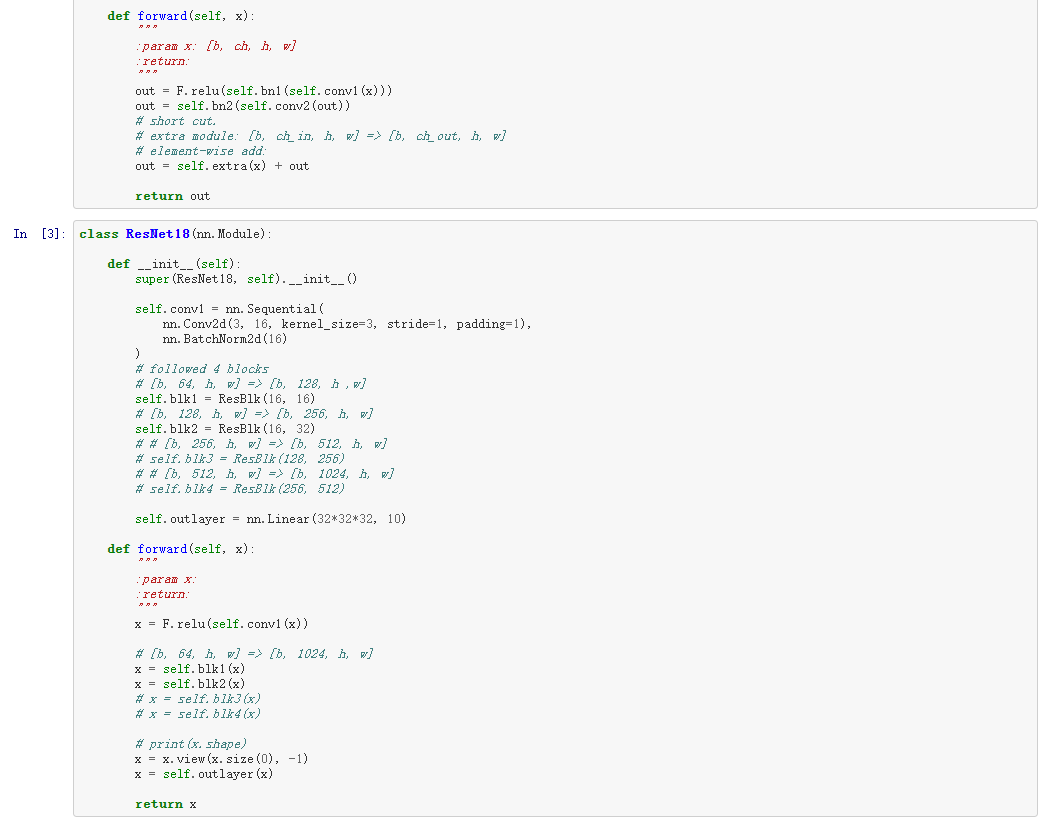
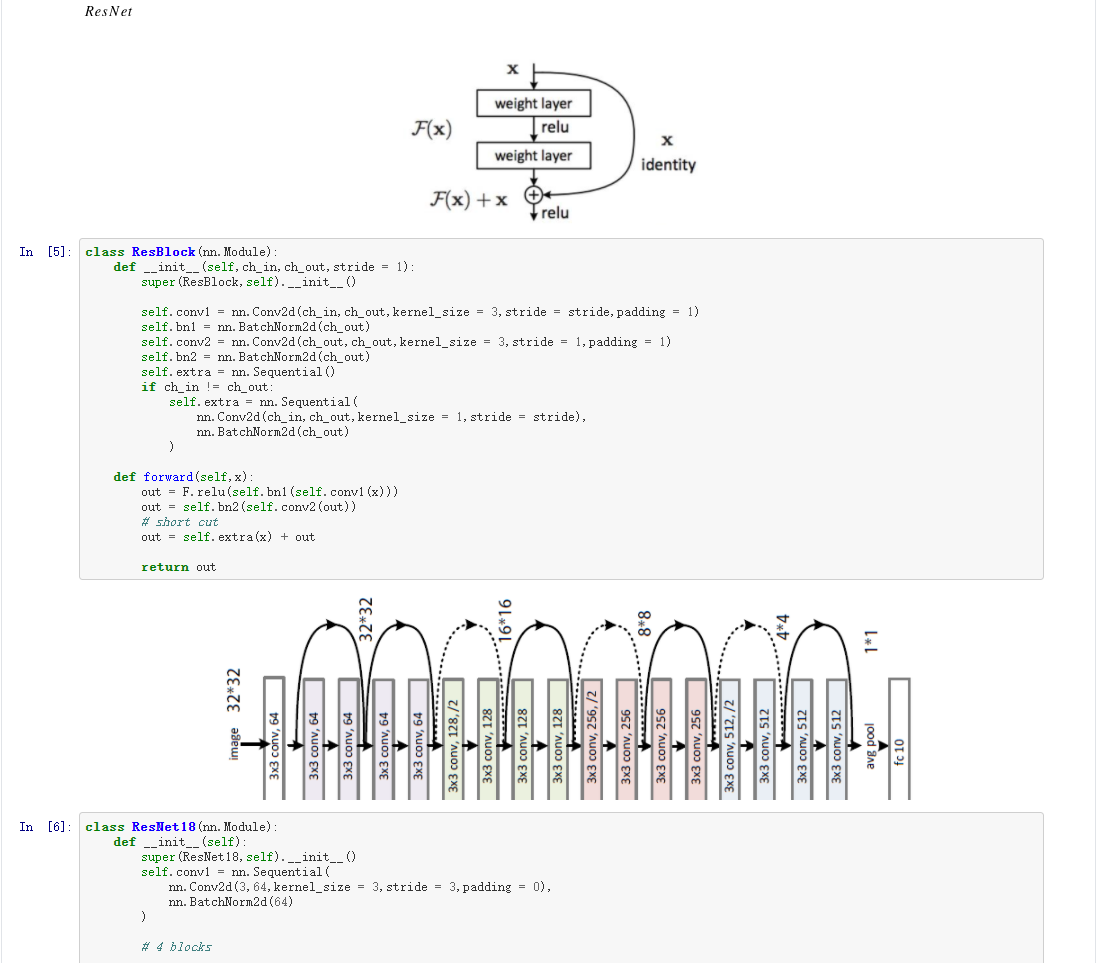
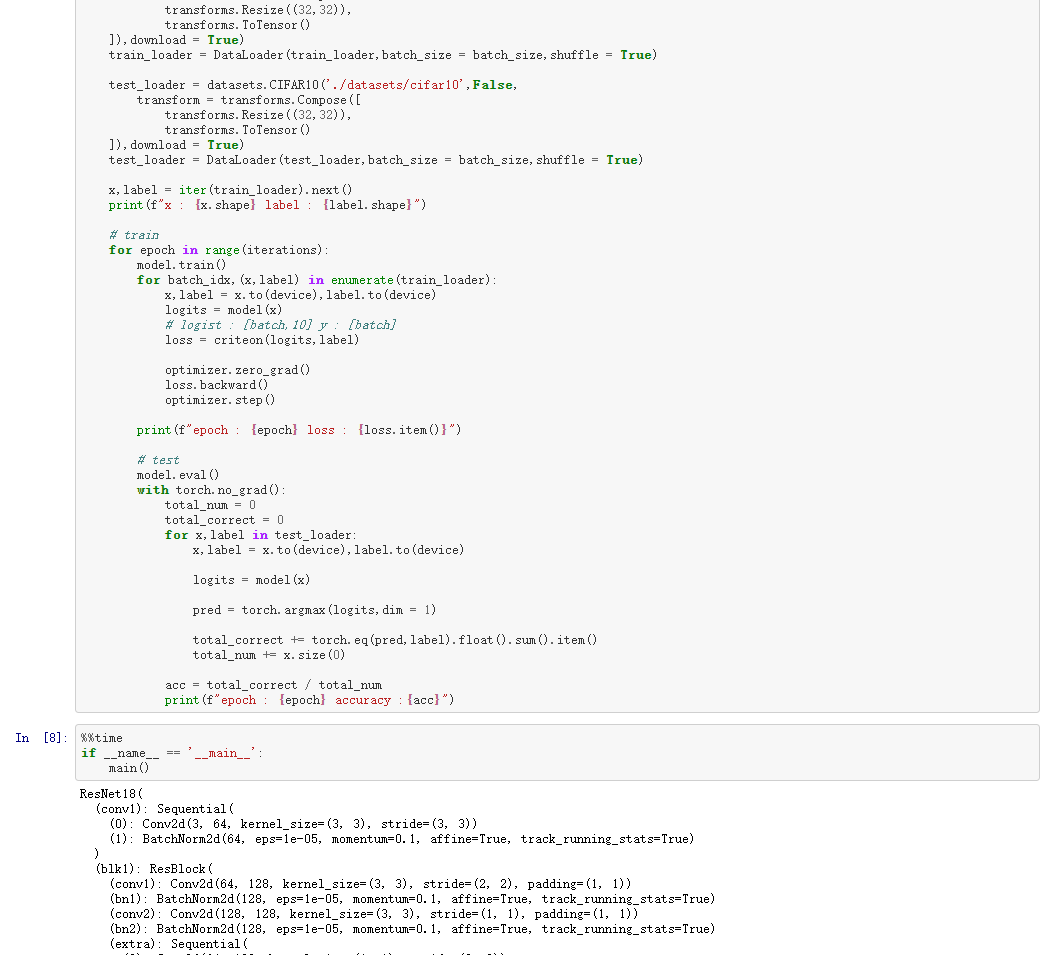
 五、ResNet

 

 

 

 六、数据增强

 

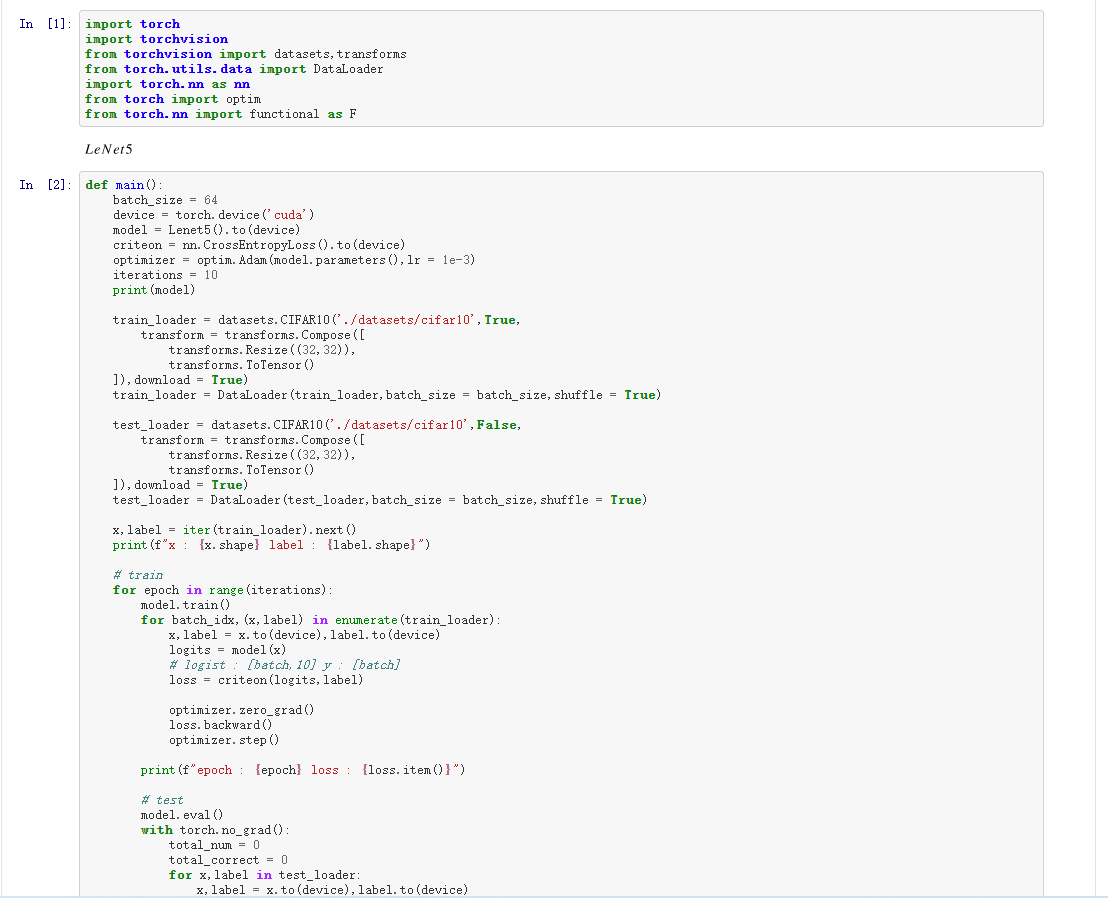
 七、CIFAR10