欧拉定理

回顾

再看一下前置知识

一定要熟悉欧拉函数的三条性质

正文

欧拉定理

若\(a\)与\(m\)互质，则\(a^{\varphi(m)}\equiv 1\pmod{m}\)。其中\(\varphi()\)为欧拉函数。

证明：设\(\leq m\)且与\(m\)互质的正整数的集合为\(T=\{x_1,x_2,x_3,...,x_{\varphi(m)}\}\)

令\(S={ax_1\%m,ax_2\%m,...,ax_{\varphi(m)}}\%m\)

任取\(i\in\{1,\varphi(m)\}\)

因为\(\gcd(a,m)=1,\gcd(x_i,m)=1\)

所以\(\gcd(ax_i,m)=1\)

所以\(\gcd(ax_i\%m,m)=1\)（辗转相除法）

因为\(S\)中的元素\(ax_i\%m\)于\(m\)互质且均小于\(m\)，所以\(S=T\)。

接下来的推导请看图

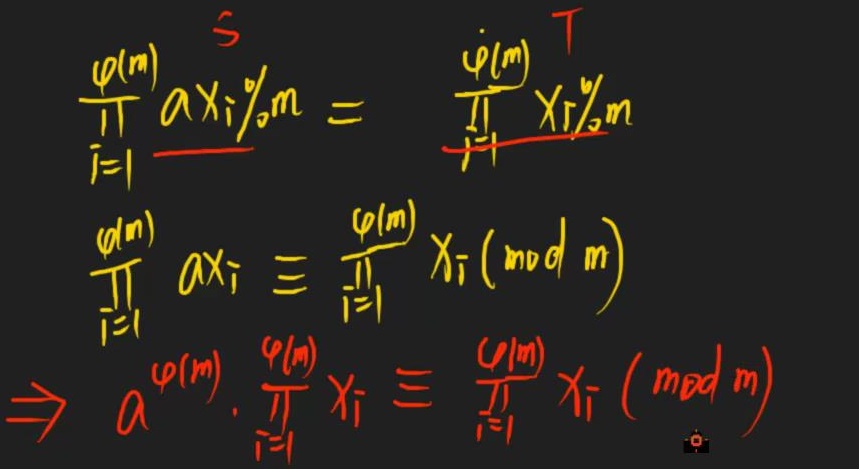
因为\(x_i\)与\(m\)互质，两边的一大坨约掉，证毕。

欧拉定理的推论

对于任意正整数\(b\)

\(a^b\equiv a^{b\%\varphi(m)}\pmod{m}\)

证明：

设\(b=q\varphi(m)+r\)，其中\(r=b\%\varphi(m)\)

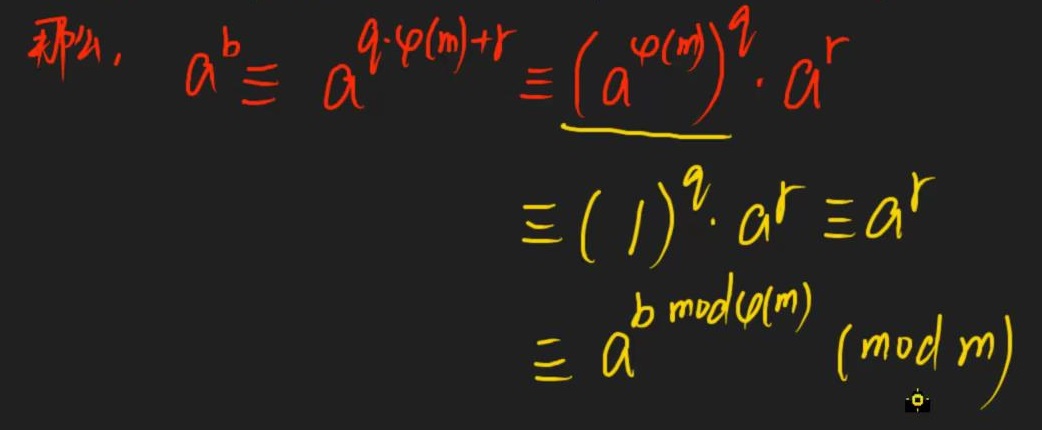
扩展欧拉定理

\(a,m\)不需要互质

若\(b\geq \varphi(m)\)，则\(a^b\equiv a^{b\%\varphi(m)+\varphi(m)}\pmod{m}\)

证明不会。

应用

当\(b\)特别大时，先对\(b\)关于\(\varphi(m)\)取模，然后再计算，对\(m\)取模

有的人会问，如果\(b<\varphi(m)\)怎么办呢？直接快速幂啊！！！

P5091 【模板】扩展欧拉定理

模板题

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn = 1e8 + 5;
int phi(int n) //欧拉函数, 也可以用O(sqrt N)的线性方法 
{
    int res = n;
    for(int i = 2; i * i <= n; i++)
    {
        if(n % i == 0)
            res = res / i * (i - 1);
        while(n % i == 0)
            n /= i;
    }
    if(n > 1)
        res = res / n * (n - 1);
    return res;
}
int qpow(int a, int b, int p) //快速幂 
{
	int res = 1;
	while(b)
	{
		if(b & 1) res = res * a % p;
		a = a * a % p;
		b >>= 1;
	}
	return res;
}
signed main()
{
	int a, m, b = 0;
	cin >> a >> m;
	char c = getchar();
	while(!isdigit(c)) c = getchar();
	int PH = phi(m);
	bool fl = false;
	while(isdigit(c))
	{
		int cur = c - '0';
		b = b * 10 + cur;
		if(b >= PH)
		{
			b %= PH;
			fl = true; //注意扩展欧拉定理的适用条件 
		}
		c = getchar();
	}
	if(fl) cout << qpow(a, b + PH, m);
	else cout << qpow(a,b,m);
	return 0;
}