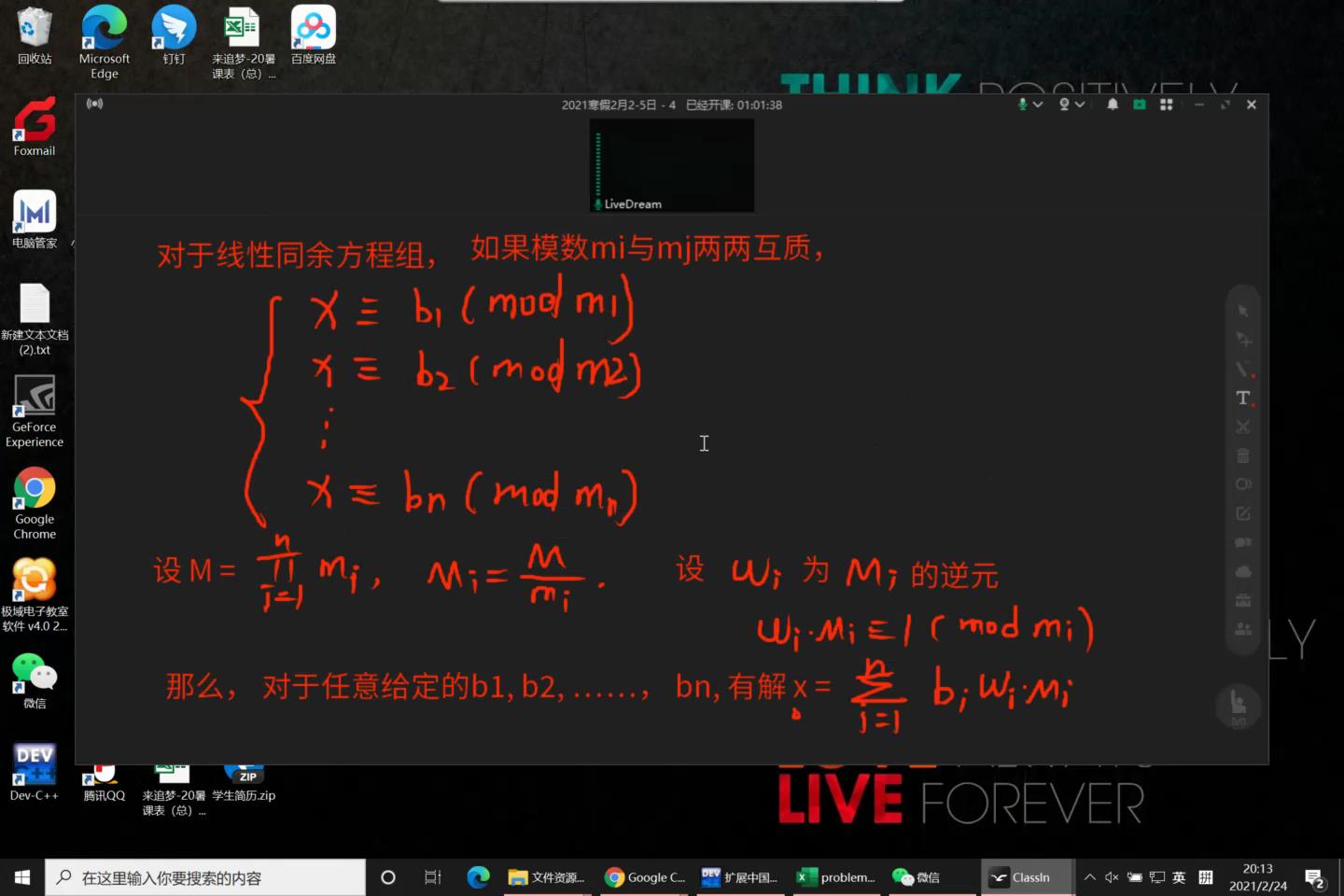
中国剩余定理和扩展中国剩余定理

中国剩余定义

应用场景

求模数互质的线性同余方程组。

三三数之余二，五五数之余三，七七数之余二

转化为数学公式为

\[\begin{cases} x\equiv 2\pmod{3}\\ x\equiv 3\pmod{5}\\ x\equiv 2\pmod{7} \end{cases} \]

证明

\[\begin{cases} x\equiv 2\pmod{3}\\ x\equiv 3\pmod{5}\\ x\equiv 2\pmod{7} \end{cases} \]

我们转化成\(n\)个互不相关的方程组。

\[\begin{cases} n_1\equiv 2\pmod{3}\\ n_2\equiv 3\pmod{5}\\ n_3\equiv 2\pmod{7} \end{cases} \]

我们想办法将\(n_1,n_2,n_3\)和\(x\)关联起来。emm

\(x=n_1+n_2+n_3\)显然不对

那么我们分别给\(n_1\)给一个\(35\)的系数（\(5\times 7\)）其他的类似。

所以我们有

\[\begin{cases} n_1=35\times m_1\\ n_2=21\times m_2\\ n_3=15\times m_3 \end{cases} \]

然后代回去得到

\[\begin{cases} 35\times m_1\equiv 2\pmod{3}\\ 21\times m_2\equiv 3\pmod{5}\\ 15\times m_3\equiv 2\pmod{7} \end{cases} \]

用逆元求一下就好了。

总结：

Code：洛谷P1495【模板】中国剩余定理(CRT)

#include <bits/stdc++.h>
#define int long long
using namespace std;
int exgcd(int a, int b, int &x, int &y)
{
	if(b == 0)
	{
		x = 1, y = 0;
		return a;
	}
	int d = exgcd(b, a % b, y, x);
	y -= (a / b) * x;
	return d;
} 
int inv(int a, int p)
{
	int x, y;
	exgcd(a, p, x, y);
	return (x % p + p) % p;
}
int CRT(vector<pair<int, int> > vec)
{
	int n = vec.size(), ans = 0;
	int M = 1;
	for(int i = 0; i < n; i ++)
		M *= vec[i].first;
	for(int i = 0; i < n; i ++)
	{
		int Mi = M / vec[i].first;
		ans += (vec[i].second * Mi * inv(Mi, vec[i].first)) % M;
	}
	return ans % M;
}
signed main()
{
	int n;
	vector<pair<int, int> > vec; // ans % first = second % first
	ios::sync_with_stdio(false);
	cin >> n;
	for(int i = 1; i <= n; i ++)
	{
		int fir, sec;
		cin >> fir >> sec;
		vec.push_back(make_pair(fir, sec));
	}
	cout << CRT(vec);
	return 0;
}

扩展中国剩余定理

应用场景

求模数不一定互质的线性同余方程组。

\[\begin{cases} x\equiv b_1\pmod{p_1}\\ x\equiv b_2\pmod{p_2}\\ x\equiv b_3\pmod{p_3}\\ ......\\ x\equiv b_n\pmod{p_n}\\ \end{cases} \]

证明

我们使用数学归纳法来证明：

首先我们只看第一个方程\(x\equiv b_1\pmod{p_1}\)

很容易得出解

假设对于前\(k\)个方程有解\(x_0\)

我们假设\(M=lcm(m_1,m_2,...,m_k)\)

我们前\(k+1\)个方程组的解显然是\(x_0\)再加上\(i\)倍的\(M\)构成，我们令它为\(x\)

那我们简单移一个项\(iM\equiv b_{k+1}-x_0\equiv{m_{k+1}}\)

我们用逆元解一下就好了，这么反复迭代，我们就可以求出最终的解了。

Code：洛谷P4777【模板】扩展中国剩余定理（EXCRT）

#include <bits/stdc++.h>
#define int long long
using namespace std;
int exgcd(int a, int b, int &x, int &y)
{
	if(b == 0)
	{
		x = 1, y = 0;
		return a;
	}
	int d = exgcd(b, a % b, y, x);
	y -= (a / b) * x;
	return d;
}
signed main()
{
	ios::sync_with_stdio(false);
	int n;
	cin >> n;
	int m, b, x, y, k;
	cin >> m >> b;
	bool flag = false;
	int lcm = m, ans = b;
	if(n == 100000 && m == 4 && b == 1) //面向数据编程，滑稽
	{
		cout << 785779359157;
		return 0;
	}
	for(int i = 2; i <= n; i ++)
	{
		cin >> m >> b;
		b = (b - ans % m + m) % m;
		int d = exgcd(lcm, m, x, y);
		if(b % d != 0)
			flag = true;
		else
			k = x * (b / d) % m;
		ans += k * lcm;
		lcm = lcm / d * m;
		ans = (ans % lcm + lcm) % lcm;
	}
	if(flag)
		cout << -1;
	else
		cout << ans;
	return 0;
}