AC自动机---好东西
前言
正文
AC自动机到底是什么呢?\(Trie+KMP\)
我们的AC自动机和KMP有什么区别呢?
AC自动机可以同时匹配很多个模式串,而KMP只可以匹配一个模式串。
那么我们来看一道例题:传送门
我们可以想到对于每一个字符串进行一次KMP,然鹅会TLE。
AC自动机就是一个算法,它可以同时进行多次KMP。
我们举一个例子:
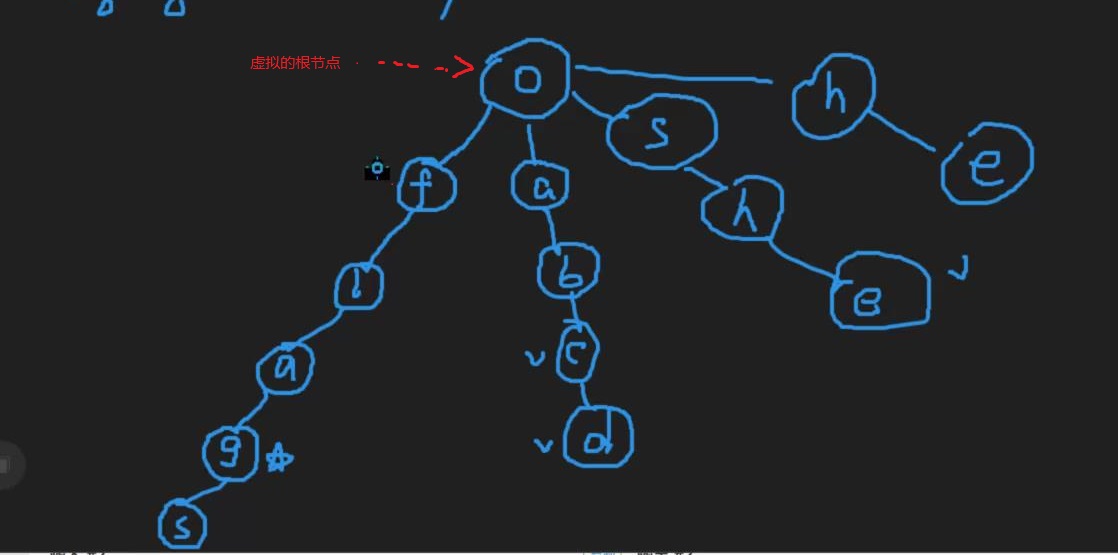
我们可以惊奇的发现:
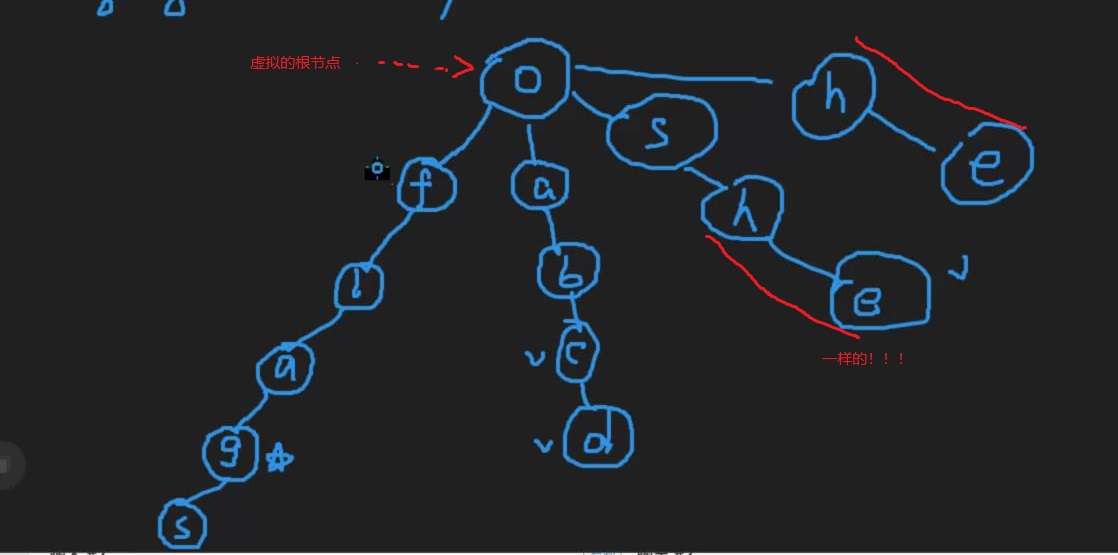
这里\(she\)的后缀\(he\),和\(he\)是一样的,这时候我们想到了什么,这和我们的KMP算法突然相似了起来?
我们可以建立一个\(fail_{cur}\)的数组,在\(she\)后的\(e\)建立一个指向\(he\)中的\(e\)的指针,和KMP中的\(next\)数组很想。像这样
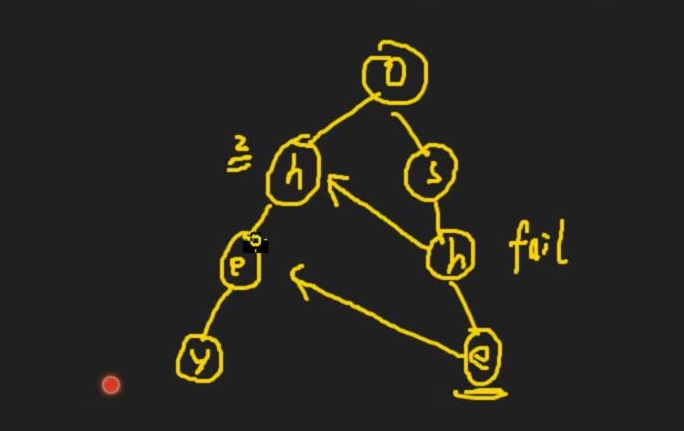
我们就可以很方便的进行匹配了。
现在我们的关键就在于如何求出\(fail\)。
我们观察到这一个\(fail\)数组是可以递归地定义地,我们想用常规方法很难给出求法
这时,我们的数学归纳法就起作用了。
数学归纳法是什么意思呢?就是假设我们的上一步已经求得结果,我们用上一步的结果来求这一个结果。我们就可以从一些基础的情况推出所有的情况了。
假设我们有一点\(trie[cur][i]\),它的父亲\(cur\),若\(cur\)的\(fail\)已经求出,那么只会有两种情况
- 我们的\(trie[cur][i]\)不为空,那么就直接把\(fail[trie[cur][i]]=fail[cur][i]\),意思就是在自己的\(fail_{cur}\)下寻找一个\(i\)代表的数组。
- 若\(trie[cur][i]\)为空,直接把这个点\(trie[cur][i]=trie[fail[cur]][i]\),直接跑到\(fail\)那里去。
这样就好了。
我们查找的时候就一个字符一个字符的找,每一次针对一个字符,不停地根据\(fail\)往上跳,直到跳不动为止。
在这个过程中,我们要注意统计一次答案,就要把\(Trie\)中的计数器\(cnt\)清空为\(-1\),代表跳到这里就跳不了了。
我们就可以轻松的打出代码
Code:
#include<iostream>
#include<queue>
using namespace std;
const int N = 1000005;
int trie[N][28], tot, num[N], fail[N];
queue<int> q;
void insert(string s)
{
int cur = 0;
for(int i = 0; i < s.size(); i++)
{
if(trie[cur][s[i]-'a'] == 0)
{
tot++;
trie[cur][s[i]-'a'] = tot;
}
cur = trie[cur][s[i]-'a'];
}
num[cur]++; //统计以cur结尾的单词出现的次数
return ;
}
void get_fail() //bfs构建fail数组
{
for(int i = 0; i < 26; i++) //根结点下面直接连的第一层结点,fail直接指向根结点0
if(trie[0][i])
q.push(trie[0][i]);
while(q.empty() == false) //队列中维护能够拓展fail值的结点
{
int cur = q.front();
q.pop();
for(int i = 0; i < 26; i++)
{
if(trie[cur][i])
{
//失配时,以trie[u][i]结尾的后缀尽量在trie中找一个与之相同的前缀(类似KMP)
fail[trie[cur][i]] = trie[fail[cur]][i];
q.push(trie[cur][i]);
}
else //节点不存在,往上连,最多回到根结点0, 注意是trie不是fail数组
trie[cur][i] = trie[fail[cur]][i];
}
}
return ;
}
int query(string t) //询问,t是文本串
{
int cur = 0, res = 0; //cur表示trie中的结点
for(int i = 0; i < t.size(); i++)
{
cur = trie[cur][t[i] - 'a']; //获取t[i]所对应的结点
for(int j = cur; j && num[j] != -1; j = fail[j])
{
res += num[j];
num[j] = -1; //标记为统计过
}
}
return res;
}
int main()
{
int n;
string s;
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> s;
insert(s);
}
cin >> s; //文本串
get_fail();
cout << query(s);
return 0;
}
扩展
P3796 【模板】AC自动机(加强版)
我们注意到这道题中题目强调了:保证不存在两个相同的模式串
这就意味着我们的\(Trie\)树中没有一个叶子节点会有两个模式串同时经过。
那么我们用\(id\)数组可以记录是哪个模式串的叶子节点。
我们在查询的时候再统计\(num\)数组
有的人会问这不会有误差吗?
没有关系,我们只关注叶子节点的\(num\)值,其它的可能会错,但是那不重要。
就好了
Code
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 1000005;
int trie[N][28], tot, num[N], fail[N], id[N], ans[N], n;
queue<int> q;
void insert(string s, int k) //k表示第几个模式串
{
int cur = 0;
for(int i = 0; i < s.size(); i++)
{
if(trie[cur][s[i]-'a'] == 0)
{
tot++;
trie[cur][s[i]-'a'] = tot;
}
cur = trie[cur][s[i]-'a'];
}
id[cur] = k;
return ;
}
void get_fail() //bfs构建fail数组
{
for(int i = 0; i < 26; i++)
{
if(trie[0][i])
q.push(trie[0][i]);
}
while(q.empty() == false)
{
int cur = q.front();
q.pop();
for(int i = 0; i < 26; i++)
{
if(trie[cur][i])
{
fail[trie[cur][i]] = trie[fail[cur]][i];
q.push(trie[cur][i]);
}
else
trie[cur][i] = trie[fail[cur]][i];
}
}
return ;
}
int query(string t) //询问
{
int cur = 0, res = 0; //cur表示trie中的结点
for(int i = 0; i < t.size(); i++)
{
cur = trie[cur][t[i] - 'a']; //获取t[i]所对应的结点
for(int j = cur; j != 0; j = fail[j])
num[j]++;
}
for(int i = 0; i <= tot; i++) //tot结点编号
{
if(id[i] != 0)
{
res = max(res, num[i]);
ans[id[i]] = num[i];
}
}
return res;
}
void work()
{
string s[155];
for(int i = 1; i <= n; i++)
{
cin >> s[i];
insert(s[i], i);
}
string ss;
cin >> ss;
get_fail();
int maxi = query(ss);
cout << maxi << "\n";
for(int i = 1; i <= n; i++)
if(ans[i] == maxi)
cout << s[i] << "\n";
return ;
}
int main()
{
while(cin >> n && n != 0)
{
memset(num, 0, sizeof(num));
memset(trie, 0, sizeof(trie));
memset(id, 0, sizeof(id));
memset(fail, 0, sizeof(fail));
tot = 0;
work();
}
return 0;
}
P5357 【模板】AC自动机(二次加强版)
二次加强版,顾名思义,它一定有一些别的要求
当我们用上一题的代码提交的话------\(TLE\)!
怎么办?注意:数据不保证任意两个模式串不相同。
在统计中,我们原本有id[cur] = k;
我们用vector<int> id[]来解决问题
但是还是会\(TLE\)
我们考虑一个极限状况,文本串和模式串都为aaaaaaa
那么它的\(fail\)数组就会指向自己的父亲。
我们的目标串每移动一个位置,我们就必须用\(fail\)数组往上跳\(n\)次。
那么为甚么会这么慢呢?原来是在上一道题目中它保证每一个模式串都不同,就不会出现这种极限的状况。
我们在这里思考一下,能不能在统计的时候只改变一次就可以了。
我们回顾一下\(fail\)数组的含义,它是记录最长的前后缀相等......
这就意味着我们只要在一个节点匹配成功,它\(fail\)数组所指向的点也会出现。
此时我们意识到\(fail\)指针构成了一个\(DAG\),我们就可以用一个树形DP来统计这一个节点对其他节点的贡献。
这就很nice了
代码实现很简单(指思路)
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N = 200005;
int trie[N][28], tot, dp[N], fail[N], id[N], ans[N], head[N], cnt, n;
queue<int> q;
struct node
{
int to, nxt;
}edges[N];
void addedge(int a, int b)
{
cnt++;
edges[cnt].to = b;
edges[cnt].nxt = head[a];
head[a] = cnt;
return ;
}
void insert(string s, int k) //k表示第几个模式串
{
int cur = 0;
for(int i = 0; i < s.size(); i++)
{
if(trie[cur][s[i]-'a'] == 0)
{
tot++;
trie[cur][s[i]-'a'] = tot;
}
cur = trie[cur][s[i]-'a'];
}
id[k] = cur; //记录第k个模式串在trie树中以cur结点结尾
return ;
}
void get_fail() //bfs构建fail数组
{
for(int i = 0; i < 26; i++)
{
if(trie[0][i])
q.push(trie[0][i]);
}
while(q.empty() == false)
{
int cur = q.front();
q.pop();
for(int i = 0; i < 26; i++)
{
if(trie[cur][i])
{
fail[trie[cur][i]] = trie[fail[cur]][i];
q.push(trie[cur][i]);
}
else
trie[cur][i] = trie[fail[cur]][i];
}
}
return ;
}
void counting(string t) //询问
{
int cur = 0; //cur表示trie中的结点
for(int i = 0; i < t.size(); i++)
{
cur = trie[cur][t[i] - 'a']; //获取t[i]所对应的结点
dp[cur]++; //cur结点经过的次数
}
return ;
}
void dfs(int cur, int fa) //树形DP, 统计子结点对父节点的贡献
{
for(int i = head[cur]; i != 0; i = edges[i].nxt)
{
int to = edges[i].to;
if(to == fa) //实际上不需要记录fa, why?
continue;
dfs(to, cur);
dp[cur] += dp[to];
}
return ;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
{
string s;
cin >> s;
insert(s, i);
}
string ss;
cin >> ss;
get_fail(); //求fail数组
counting(ss); //统计每个结点经过的次数,但是不再用fail跳
//由fail数组建边, 做树形DP, 统计每个点的子树对其自身的贡献
for(int i = 1; i <= tot; i++)
addedge(fail[i], i);
dfs(0, -1); //树形DP
for(int i = 1; i <= n; i++) //输出每个模式串i对应的trie结点id[i]被经过的次数dp[id[i]]
cout << dp[id[i]] << "\n";
return 0;
}
这道题给我们了一些启发
- AC自动机除了一颗\(Trie\)树之外,还有一个\(fail\)树
- 所以我们可以将树上DP,树上查分,莫队,甚至树链剖分和AC自动机结合起来形成一些毒瘤的题目
P3041 [USACO12JAN]Video Game G
这道题很好!!!
我们很容易的想出这个问题的子问题,文本串长度为\(k-1,k-2......\)
我们想到DP,定义\(dp_i\)表示长度为\(i\)的文本串能够得到的最大得分
但是这样不好转移,我们就增加一维\(dp_{i,j}\)表示字符串长度为\(i\)且在\(Trie\)树中\(j\)节点
状态伪代码
dp[i][trie[j][c]]=max(dp[i][trie[j][c]], dp[i-1][j]+val[trie[j][c]]);
这样定义我们能跑树形DP了吗?不能,这个状态有两维,有后效性
我们可以用树形DP来预处理,就是在GetFail函数中加一行val[cur]+=val[fail[cur]]
就可以啦!!!!
#include <bits/stdc++.h>
using namespace std;
const int MX = 305;
int trie[MX][26], fail[MX], val[MX], total, n, k, dp[1005][MX];
void ins(string s)
{
int len = s.size(), cur = 0;
for(int i = 0; i < len; i ++)
{
int to = s[i] - 'A';
if(trie[cur][to] == 0)
trie[cur][to] = ++ total;
cur = trie[cur][to];
}
val[cur] ++;
return ;
}
void GetFail()
{
queue<int> q;
for(int i = 0; i < 3; i++)
{
if(trie[0][i])
q.push(trie[0][i]);
}
while(q.empty() == false)
{
int cur = q.front();
q.pop();
for(int i = 0; i < 3; i++)
{
if(trie[cur][i])
{
fail[trie[cur][i]] = trie[fail[cur]][i];
q.push(trie[cur][i]);
}
else
trie[cur][i] = trie[fail[cur]][i];
}
val[cur] += val[fail[cur]];
}
return ;
}
void DP(int k)
{
memset(dp, 0xcf, sizeof(dp));
for(int i = 0; i <= k; i++)
dp[i][0] = 0;
for(int i = 1; i <= k; i++)
for(int j = 0; j <= total; j++)
for(int c = 0; c < 3; c++)
dp[i][trie[j][c]] = max(dp[i][trie[j][c]], dp[i-1][j] + val[trie[j][c]]);
return ;
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> k;
for(int i = 1; i <= n; i ++)
{
string s;
cin >> s;
ins(s);
}
GetFail();
DP(k);
int anss = INT_MIN;
for(int i = 0; i <= total; i ++)
anss = max(dp[k][i], anss);
cout << anss;
return 0;
}
总结
AC自动机是一个好东西!!!!
题目清单:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号