可持久化字典树学习笔记

引子

我们回忆一下，可持久化可以解决哪些问题？

我们通常用可持久化来解决区间询问，将区间转化成历史版本

可持久化字典树

加入我们有\(4\)个单词\(cxc,cxd,cyc,cyt\)

我们用每一个版本代表插入之后的字典树，我们就得到了如下的图。

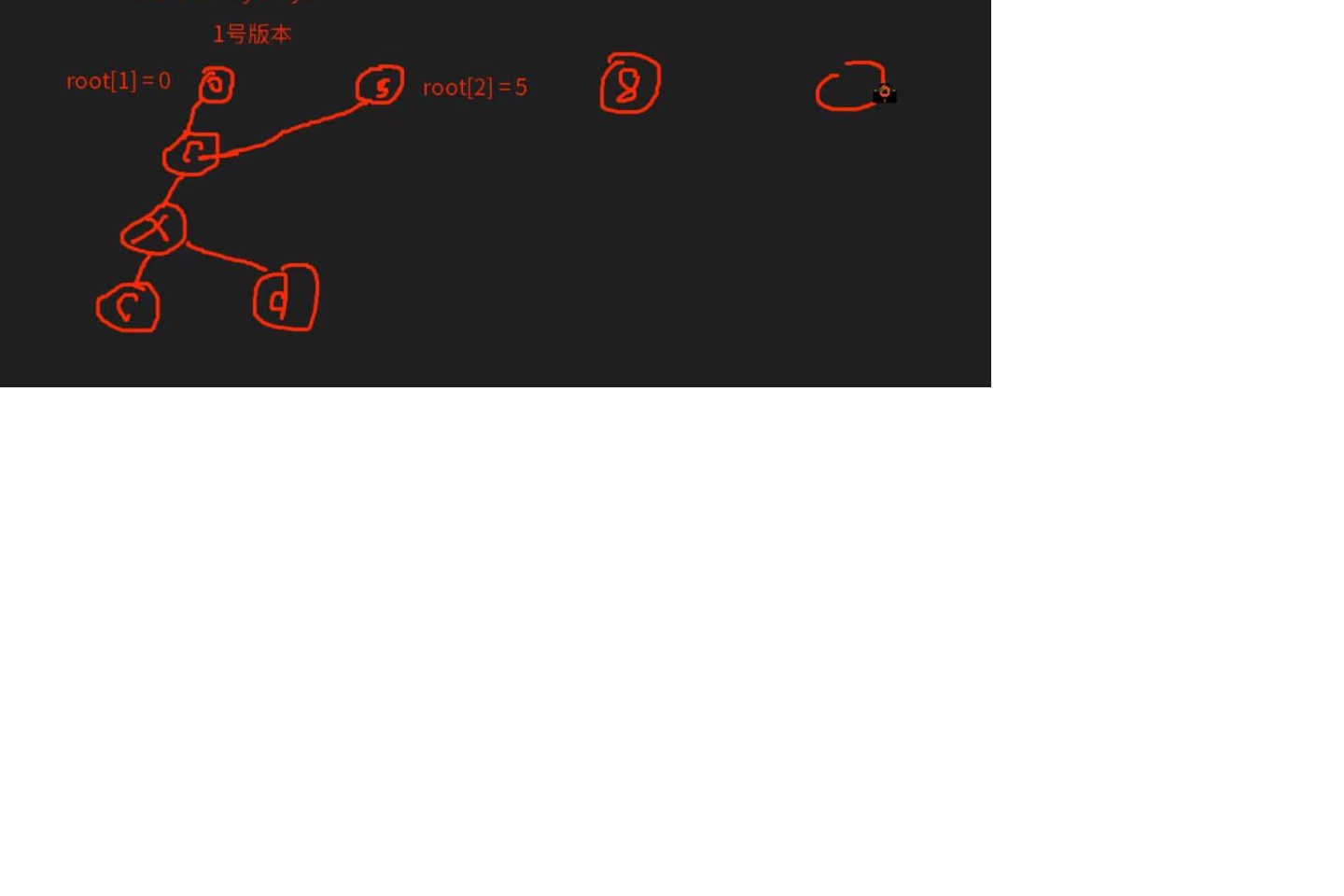
类似的，我们也可以得到可持久化01字典树建树的方法

例题

最大异或和

我们首先想到前缀和，所以我们用一个01trie树维护异或的前缀和，然后考虑询问

对于右端点，我们直接以\(root_r\)为根来进行查找

关键是左端点，我们对于每一个节点，我们记录一个\(last_i\)数组，表示以\(i\)为根节点时，最大的版本编号。

这时我们在查找的时候判断一下，这个节点的\(last\)是否低于\(l\)。

我们就可以轻松的打出这样代码

#include<iostream>
using namespace std;
const int N = 600010;
int trie[N * 24][2], last[N * 24]; // last[i]表示结点以i为根节点的子树中最大的版本编号 
int s[N], root[N], n, m, tot;


void insert(int i, int k, int p, int q) //第i个串s[i]的第k位， p是上一个版本， q是当前版本 
{
    if(k < 0) 
    {
        last[q] = i; //第i个字符串出现的最后一个版本（版本最后会转化成s序列的区间） 
        return;
    }
    int c = s[i] >> k & 1;
    if(p) 
        trie[q][c ^ 1] = trie[p][c ^ 1]; //只有0，1两个孩子，q自己的孩子是c，则连到p的是c^1 
    trie[q][c] = ++tot; //新建结点 
    insert(i, k - 1, trie[p][c], trie[q][c]);
    last[q] = last[trie[q][c]];
    return ;
}

int query(int cur, int val, int k, int left) //left左边界 
{
    if(k < 0) //二进制数位到最低位 
        return s[last[cur]] ^ val;
    int c = val >> k & 1;
    if(last[trie[cur][c ^ 1]] >= left)
        return query(trie[cur][c ^ 1], val, k - 1, left);
    return query(trie[cur][c], val, k - 1, left);
}

int main() 
{
    cin >> n >> m;
    last[0] = -1;
    tot = 1;
    root[0] = tot;
    insert(0, 23, 0, root[0]);
    for(int i = 1; i <= n; i++) 
    {
        int x;
        cin >> x;
        s[i] = s[i - 1] ^ x;
        root[i] = ++tot;
        insert(i, 23, root[i - 1], root[i]); //10^7次方的底数23 
    }
    for(int i = 1; i <= m; i++) 
    {
        string op;
        cin >> op;
        if(op == "A") 
        {
            int x; 
            cin >> x;
            root[++n] = ++tot;
            s[n] = s[n - 1] ^ x;
            insert(n, 23, root[n - 1], root[n]);
        }
        else 
        {
            int l, r, x;
            cin >> l >> r >> x; 
            cout << query(root[r - 1], x ^ s[n], 23, l - 1) << "\n";
        }
    }
    return 0; 
}