Kruskal 重构树学习笔记

Kruskal 重构树学习笔记

可以干什么

求那些最大值最小，或者最小值最大

如何实现

在Kruskal最小生成树中加入一些东西，比如

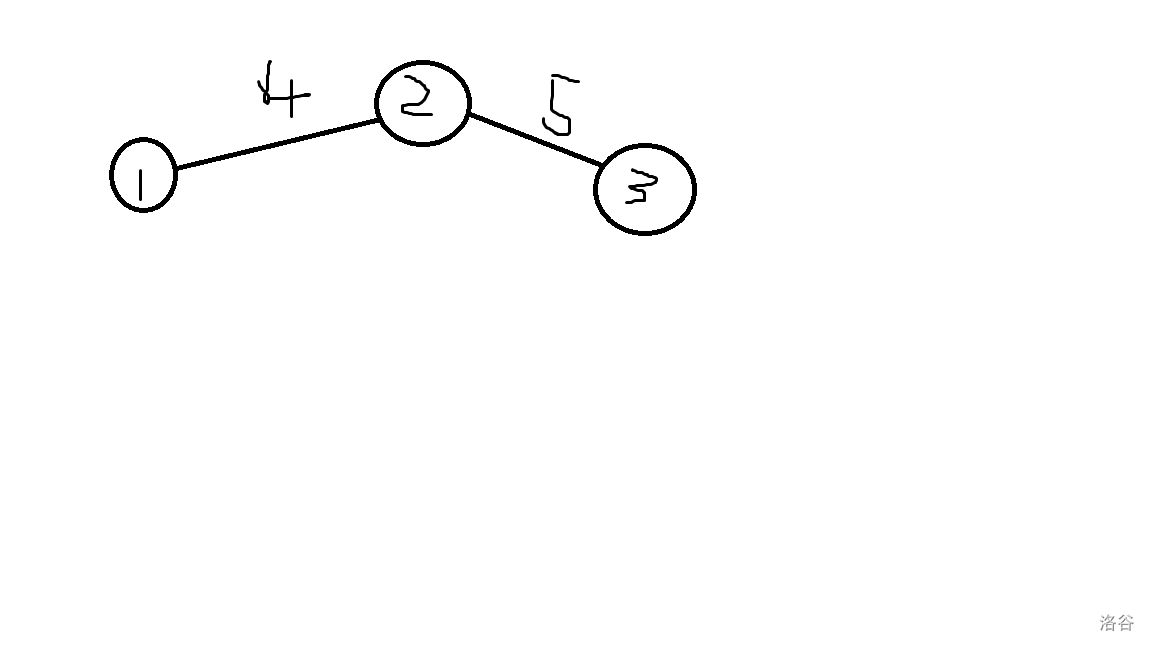
这时，我们在做最小生成树的时候，加入一个神奇的建树，就会得到：

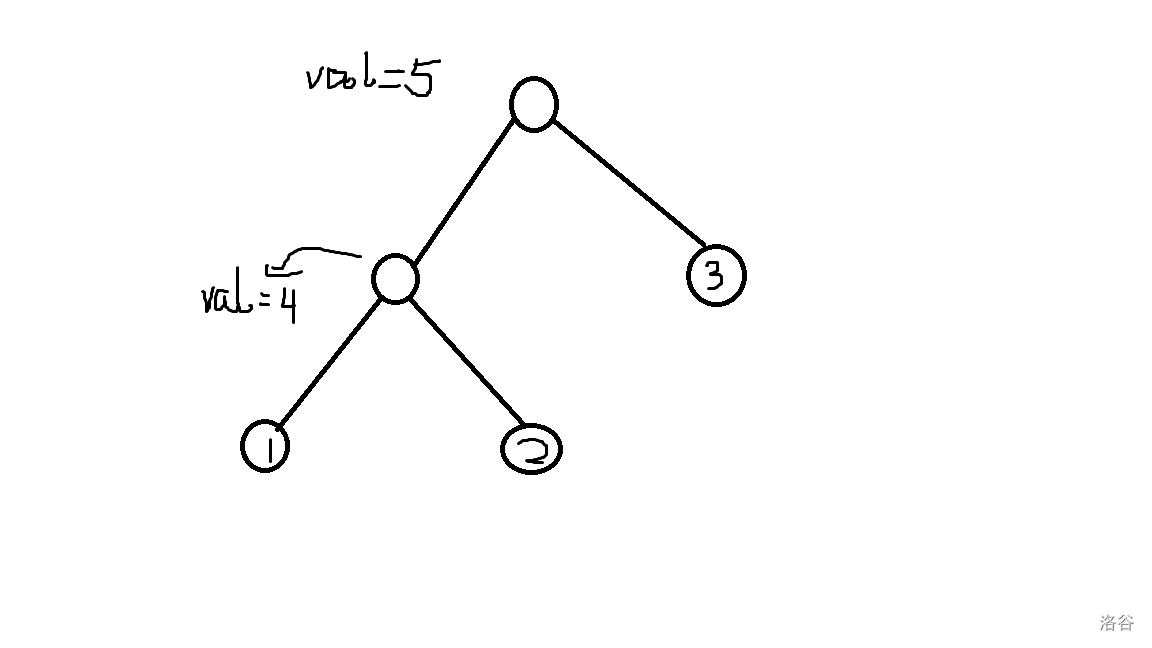
此时我们要求2到3的路径上的最大边权是\(lca(2,3)\)的\(val\)值。

这就很香了，如果要求最小值怎么办，我们就做最大生成树就好了。

阿巴阿巴

例题

luogu P1967 货车运输

板子题，直接上代码。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 500005;
int n, m, s, cnt, point;
int head[maxn], d[maxn], dp[maxn][21], lg[maxn], fa[maxn], val[maxn]; 
struct node
{
    int to, next;
}e[2 * maxn]; 

struct edge
{
	int x, y, z;
}edges[maxn];

void add_edge(int u, int v)
{
    e[cnt].to = v;
    e[cnt].next = head[u];
    head[u] = cnt;
	cnt++;
    return;
}               

void pre_process(int cur, int father)  
{
    d[cur] = d[father] + 1;  
    dp[cur][0] = father; 
    for(int i = 1; (1 << i) <= d[cur]; i++)
        dp[cur][i] = dp[dp[cur][i-1]][i-1];  
    for(int i = head[cur]; i != -1; i = e[i].next)
    {
        int v = e[i].to;  
        if(v != father)  
        	pre_process(v, cur);
    }
    return ;
}                               

int lca(int a, int b)  
{
    if(d[a] > d[b])
		swap(a, b); 
    for(int i = lg[n]; i >= 0; i--)   
        if(d[a] <= d[b] - (1 << i))  
            b = dp[b][i];       
    if(a == b)
        return a;                 
    for(int i = lg[n]; i >= 0; i--)
        if(dp[a][i] != dp[b][i])
        {
        	a = dp[a][i];
			b = dp[b][i]; 
		}
    return dp[a][0];  
}

bool cmp(edge a, edge b)
{
    return a.z > b.z;
}

int find(int x)
{
	if(fa[x] == x)
		return x;
	return fa[x] = find(fa[x]);
}

void kruskal()
{
	point = n; 
	for(int i = 1; i <= n; i++)
		fa[i] = i;
    sort(edges + 1, edges + m + 1, cmp); 
    for(int i = 1; i <= m; i++)
    {
        int a = find(edges[i].x); 
		int b = find(edges[i].y); 
        if(a != b) 
        {
            point++;
            val[point] = edges[i].z;
            fa[a] = fa[b] = fa[point] = point;
            add_edge(a, point);
            add_edge(point, a);
            add_edge(b, point);
            add_edge(point, b);
        }
    }
    return ;
}

int main()
{
	cin >> n >> m;
	for(int i = 1; i <= m; i++)
		cin >> edges[i].x >> edges[i].y >> edges[i].z;
	memset(head, -1, sizeof(head));
	kruskal();
	lg[0] = -1;
	for(int i = 1; i <= point; i++)
	{
		lg[i] = lg[i >> 1] + 1;
	}
	
	pre_process(point, 0);
	int q; 
	cin >> q;
	for(int i = 1; i <= q; i++)
	{
		int x, y;
		cin >> x >> y;
		if(find(x) != find(y))
			cout << -1 << endl;
		else
		{
			int tmp = lca(x, y);
		cout << val[tmp] << endl;
		}
	}
	return 0;
}