《数据结构与算法分析-C语言描述》第三章 表、栈和队列 学习笔记
前言->本章重点:
1.介绍抽象数据类型(ADT的概念)
2.阐述如何对表进行有效的操作
3.介绍栈ADT及其在实现递归方面的应用
4.介绍队列ADT及其在操作系统和算法设计中的应用
3.1 抽象数据类型
抽象数据类型(abstract data type,ADT)是一些操作的集合。抽象数据类型是数学的抽象:在ADT的定义中根本没涉及如何实现操作的集合。这可以看作是模块化设计的扩充。
3.2 表ADT
我们将处理一般的形如A1,A2,A3...An的表。我们说,这个表的大小是N,我们称大小为0的表为空表(empty list)。
现在我们讨论 在表ADT上进行的操作的集合。PrintList和MakeEmpty是常用的操作,其功能显而易见;Find返回关键字首次出现的位置;Insert和Delete一般是从表的某个位置插人和删除某个关键字;而FindKth 则返回某个位置上(作为参数而被指定)的元素。
3.2.1 表的简单数组实现
局限性:数组的大小一旦确定就无法改变,通常需要估计的大一些,从而会浪费大量的空间,这是严重的局限,特别是针对于许多未知大小的表。
执行时间:
PrintList和Find为O(n),FindKth为O(1),而Insert和Delete:最坏为O(n),花费是昂贵的,例如,在位置0的插人(这实际上是做一个新的第一元素)首先需要将整个数组后移一个位置以空出空间来,而删除第一个元素则需要将表中的所有元素前移一个位置,因此这两种操作的最坏情况为O(N)。
分析:因为插入和删除的运行时间是如此的慢以及表的大小还必须事先已知,所以简单数组一般不用来实现表这种结构。
3.2.2 链表
引入:为了避免插入和删除的线性开销,我们允许表可以不连续存储。
定义:链表由一系列不必在内存中相连的结构组成。每一个结构均含有表元素和指向包含该元素后继元的结构的指针。我们称之为Next指针。最后一个单元的Next 指针指向 NULL;该值由C定义并且不能与其他指针混淆。ANSI C规定 NULL为零。

执行时间:
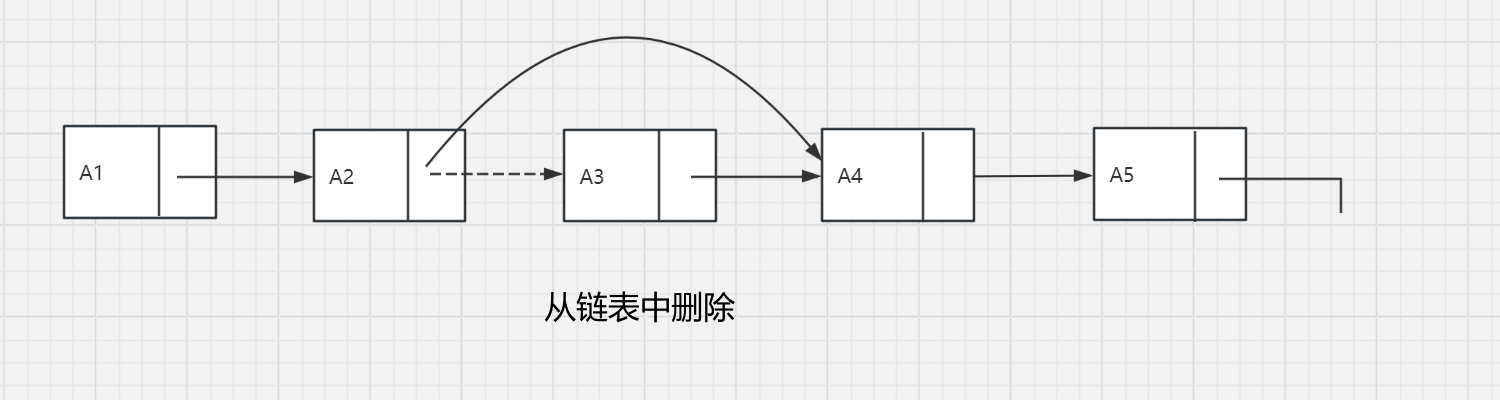
PrintList和Find为O(n),FindKth为O(n)。而Delete可以通过修改一个指针实现,Insert需要使用一次malloc调用从系统中得到一个新单元,并进行两次指针调整。如下图所示。

3.2.3 程序设计实现
head指针的引入:上面的描述存在一些问题,第一,并不存在从所给定义出发在表的前面插入元素的真正显性的方法。第二,从表的前面实行删除是一个特殊情况,因为它改变了表的起始端;编程中的疏忽将会造成表的丢失。第三个问题涉及一般的删除。虽然上述指针的移动很简单,但是删除算法要求我们记住被删除元素前面的表元。
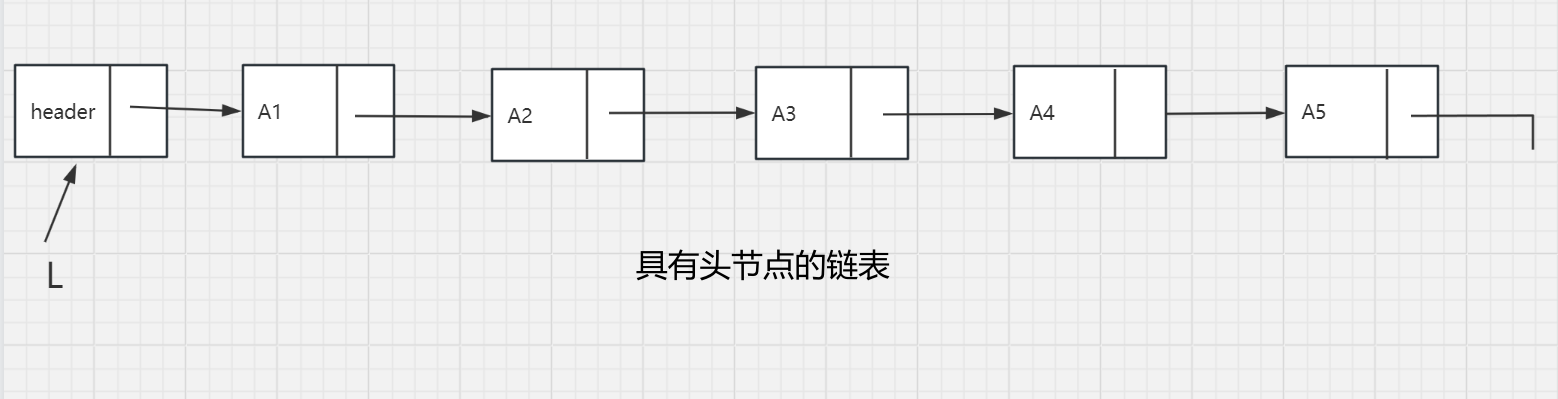
ADT的例程:
/*list.h*/
#ifndef _LIST_H
typedef int ElementType;
struct Node;
typedef struct Node * PtrToNode;
typedef PtrToNode List;
typedef PtrToNode Position;
List MakeEmpty(List L);//生成一个空链表
int IsEmpty(List L);//判断是否为空链表
int IsLast(List L,Position P);//判断是否是最后一个节点
Position Find(List L,ElementType X);//查找含有元素X的结点
Position FindPrevious(List L,ElementType X); //查找含有元素X的结点的前驱元
void Insert(List L,Position P,ElementType X);//在P位置之后,插入一个元素为X的结点
void Delete(List L,Position P);//删除P结点
void DeleteList(List L);//删除链表
Position Header(List L);//返回表头结点
Position First(List L);//返回第一个结点
Position Advance(Position P); //返回P结点的后继元
ElementType Retrieve(Position P);//返回P结点的元素
#endif
struct Node{
ElementType Element;
Position Next;
};
/*list.c*/
# include "list.h"
# include <stdlib.h>
# include <stdio.h>
//生成一个空链表
List MakeEmpty(List L){
if (L != NULL) {
DeleteList(L);
}else{
L = (List)malloc(sizeof(struct Node));
if(L==NULL){
printf("out of space!\n");
exit(1);
}
L->Next=NULL;
}
return L;
}
//判断是否为空链表
int IsEmpty(List L){
return L->Next == NULL;
}
//判断是否是最后一个节点
int IsLast(List L,Position P){
return P->Next == NULL;
}
//查找含有元素X的结点(找不到P为NULL)
Position Find(List L,ElementType X){
Position P = L->Next;
while(P && P->Element!=X){
P = P->Next;
}
return P;
}
//查找含有元素X的结点的前驱元 (找不到P为最后一个元素)
Position FindPrevious(List L,ElementType X){
Position P = L;
while(P->Next && P->Next->Element!=X){
P = P->Next;
}
return P;
}
//在P位置之后,插入一个元素为X的结点
void Insert(List L,Position P,ElementType X){
Position TempCell;
TempCell = (Position)malloc(sizeof(struct Node));
if (TempCell == NULL) {
printf("out of space!\n");
exit(1);
}
TempCell->Element = X;
TempCell->Next = P->Next;
P->Next = TempCell;
}
//删除P结点
void Delete(List L,ElementType X){
Position PreviousCell,TmpCell;
PreviousCell = FindPrevious(L,X);
if(!IsLast(L,PreviousCell)){
TmpCell = PreviousCell->Next;
PreviousCell->Next=TmpCell->Next;
free(TmpCell);
}
}
//删除链表(表头还在)
void DeleteList(List L){
Position P = L->Next;
Position TempCell;
while(P!=NULL){
TempCell = P->Next;
free(P);
P=TempCell;
}
}
//返回表头结点
Position Header(List L){
return L;
}
//返回第一个结点
Position First(List L){
return L->Next;
}
//返回P结点的后继元
Position Advance(Position P){
return P->Next;
}
//返回P结点的元素
ElementType Retrieve(Position P){
return P->Element;
}
3.2.4 常见的错误
1."memory access violation"或"segmentation violation",这种信息通常意味着有指针变量包含了伪地址。一种情况是未初始化变量P就直接使用,P未定义就不可能指向内存中的有效部分;一种情况是如果P是Null,那么指向是非法的。
2.何时使用或何时不使用malloc来获取一个新的单元。我们必须记住,声明指向一个结构的指针并不创建该结构,而只是给出足够的空间容纳结构可能会使用的地址。创建尚未被声明过的记录的惟一方法是使用malloc库函数。
警告:malloc(sizeof(PtrToNode))是合法的,但是它并不给结构体分配足够的空间。它只给指针分配一个空间。
3.2.5 双链表
引入:为了实现倒叙扫描链表,另外,简化了删除操作,我们不需要找到前驱元。

3.2.6 循环链表
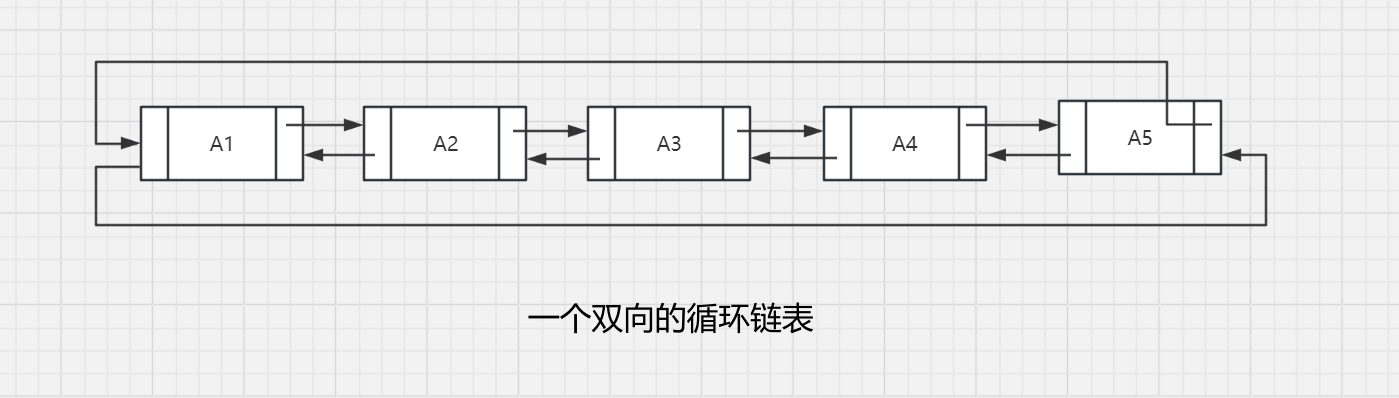
让最后的单元反过来直指第一个单元是一种流行的做法。它可以有表头,也可以没有表头(若有表头,则最后的单元就指向它),并且还可以是双向链表(第一个单元的前驱元指针指向最后的单元)。图3-17 显示了一个无表头的双向循环链表。
3.2.7 三个使用链表的例子
1.多项式
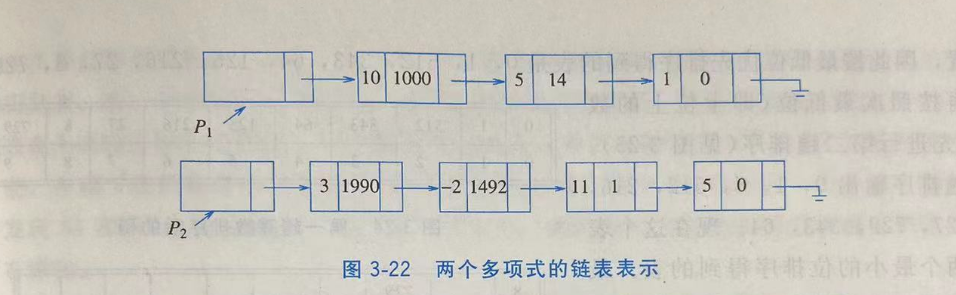
我们可以用表来定义一种关于一元(具有非负次幂)多项式的抽象数据类型。令$F(X) = \sum_{i=0}NA_iX$。如果大部分系数非零,那么我们可以用一个简单数组来存储这些系数。然后可以编写一些对多项式进行加、减、乘、微分及其他操作的例程。
但如果P(X)=10X1000+5X14+1,且P(X)=3X1990-2X1492+ 11X + 5,那么运行时间就可能不可接受了。可以看出,大部分的时间都花在了乘以0和单步调试两个输人多项式的大量不存在的部分上。这总是我们不愿看到的。
数组实现
//多项式ADT的数组实现的类型声明
typedef struct{
int CoeffArray[ MaxDegree+1];
int HighPower;//最高次幂
} * Polynomial;
//将多项式初始化为零
void ZeroPolynomial(Polynomial Poly){
int i;
for(i=0;i<=MaxDegree;i++){
Poly->CoeffArray[i]=0;
}
Poly->HighPower=0;
}
//两个多项式相加
void AddPolynomial(const Polynomial Poly1,const Polynomial Poly2,Polynomial PolySum){
int i;
ZeroPolynomial(PolySum);
PolySum->HighPower=Max(Poly1->HighPower,Poly2->HighPower);
for(i=0;i<=PolySum->HighPower;i++){
PolySum->CoeffArray[i]=Poly1->CoeffArray[i]+Poly2->CoeffArray[i];
}
}
//两个多项式相乘
void MultPolynomial(const Polynomial Poly1,const Polynomial Poly2,Polynomial PolyMult){
int i,j;
ZeroPolynomial(PolyMult);
PolyMult->HighPower=Poly1->HighPower+Poly2->HighPower;
for(i=0;i<=Poly1->HighPower;i++){
for(j=0;i<=Poly2->HighPower;i++){
PolyMult->CoeffArray[i+j]+=Poly1->CoeffArray[i]*Poly2->CoeffArray[j];
}
}
}
单链表实现(但这个时候,相乘或者相加要注意合并同类项)
//多项式ADT的链表表示
typedef struct Node *PtrToNode;
struct Node {
int Coefficient;//系数
int Exponent;//指数
PtrToNode Next;
};
typedef PtrToNode Polynomial;
2.基数排序
使用链表的第二个例子叫做基数排序(radix sort)。基数排序有时也称为卡式排序(card sort),因为直到现代计算机出现之前,它一直用于对老式穿孔卡的排序。
如果我们有N个整数,范围从1到M(或从0到M-1),我们可以利用这个信息得到一种快速的排序,叫做桶式排序(bucket sort)。我们留置一个数组,称之为 Count,大小为M,并初始化为零。于是,Count有M个单元(或桶),开始时他们都是空的。当Ai被读入时Count[Ai]增1。在所有的输人被读进以后,扫描数组Gount,打印输出排好序的表。该算法花费O(M+N)。
基数排序是这种方法的推广。了解方法含义的最容易的方式就是举例说明。设我们有10个数,范围在0到999之间,我们将其排序。一般说来,这是0到N^P-1间的N个数,P是某个常数。显然,我们不能使用桶式排序,那样桶就太多了。我们的策略是使用多趟桶式排序。
我们用最低(有效)“位”优先的方式进行桶式排序。有可能多于一个数落入相同的桶中,但有别于原始的桶式排序,这些数可能不同,因此我们把它们放到一个表中。注意,所有的数可能都有某位数字,因此如果使用简单数组表示表,那么每个数组必然大小为N,总的空间需求是 O(N^2)。下面例子说明10个数的桶式排序的具体做法。
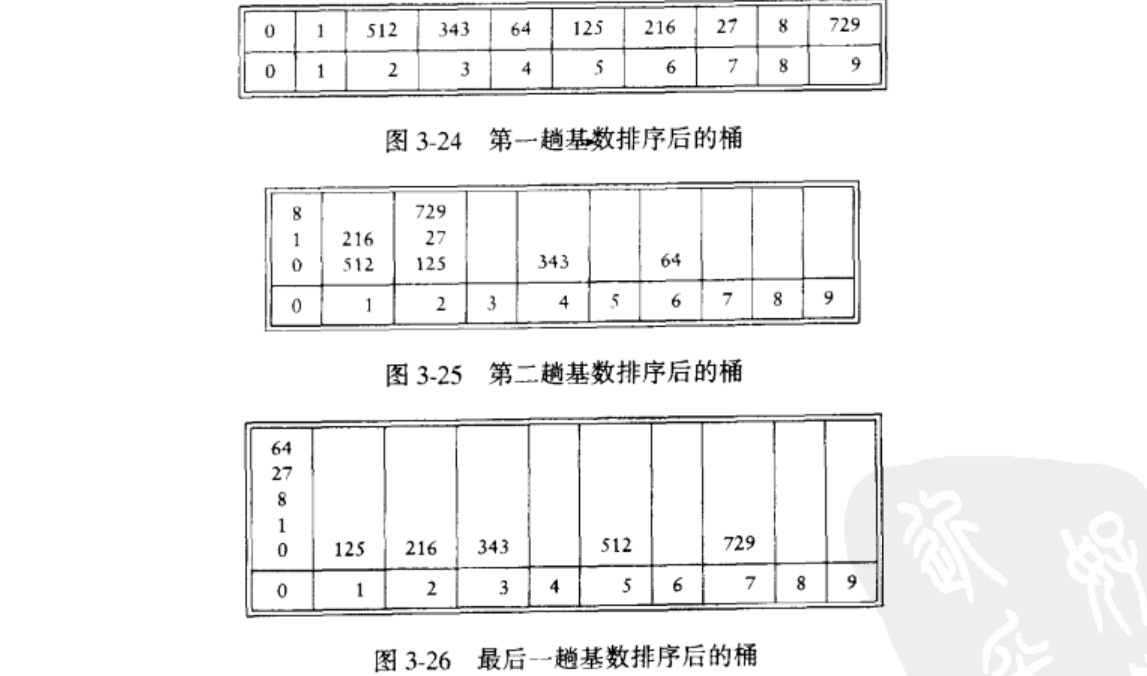
为使算法能够得出正确的结果,要注意唯一出错的可能是如果两个数出自同一个桶但顺序却是错误的。不过,前面各趟排序保证了当几个数进入一个桶的时候,它们是以排序的顺序进入的。该排序的运行时间是O(P(N+B)),其中P是排序的趟数,N是要被排序的元素的个数,而B是桶数。本例中,B=N。
3.多重表
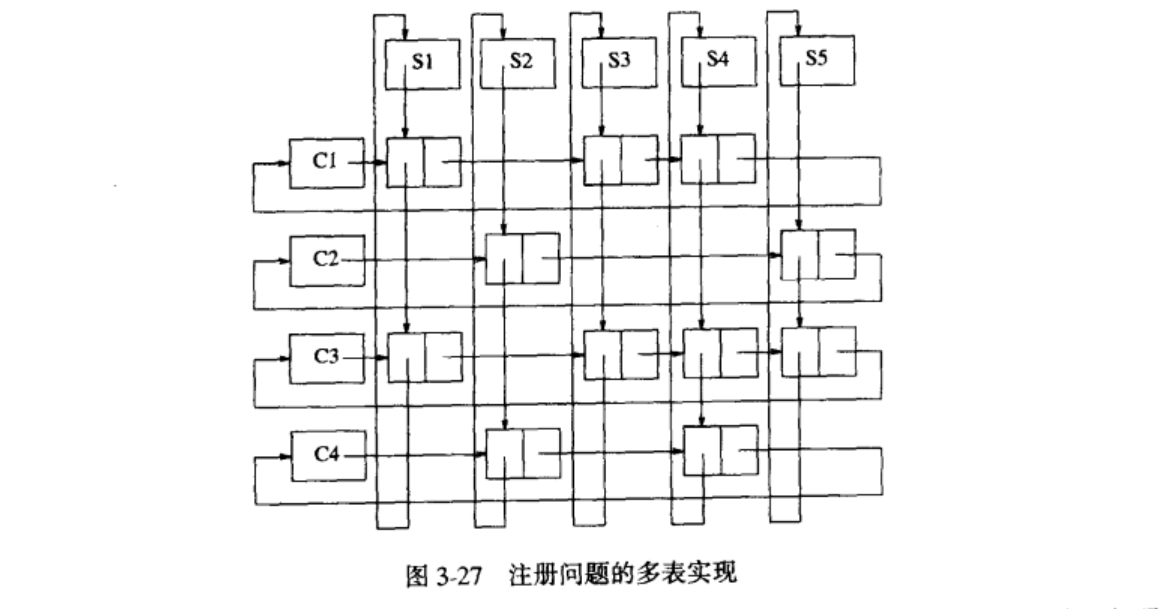
我们的最后一个例子阐述链表的更复杂的应用。一所有40000名学生和2500门课程的大学需要生成两种类型的报告。第一个报告列出每个课程的注册者,第二个报告列出每个学生注册的课程。
常用的实现方法是使用二维数组。这样一个数组将有1亿项。平均大约一个学生注册三门课程,因此实际上有意义的数据只有120000项,大约占0.1%。现在需要的是列出每个课程及每个课程所包含的学生的表。我们也需要每个学生及其每个学生所注册的课程的表。图 3-27 显示实现的方法。
3.2.8 链表的游标实现
诸如BASIC和FORTRAN等许多语言都不支持指针。如果需要链表而又不能使用指针,那么就必须使用另外的实现方法。我们将描述这种方法并称为游标(cursor)实现法。
在链表的指针实现中有两个重要的特点:
1.数据存储在一组结构体中。每一个结构体包含有数据以及指向下一个结构体的指针。
2.一个新的结构体可以通过调用malloc而从系统全局内存(global memory)得到,并可通过调用 free 而被释放。
游标法必须能够模仿实现这两条特性。满足条件1的逻辑方法是要有一个全局的结构体数组。对于该数组中的任何单元,其数组下标可以用来代表一个地址。下面给出链表游标实现的声明。
struct Node{
ElementType Element;
Position Next;
};
struct Node CursorSpace[SpaceSize];
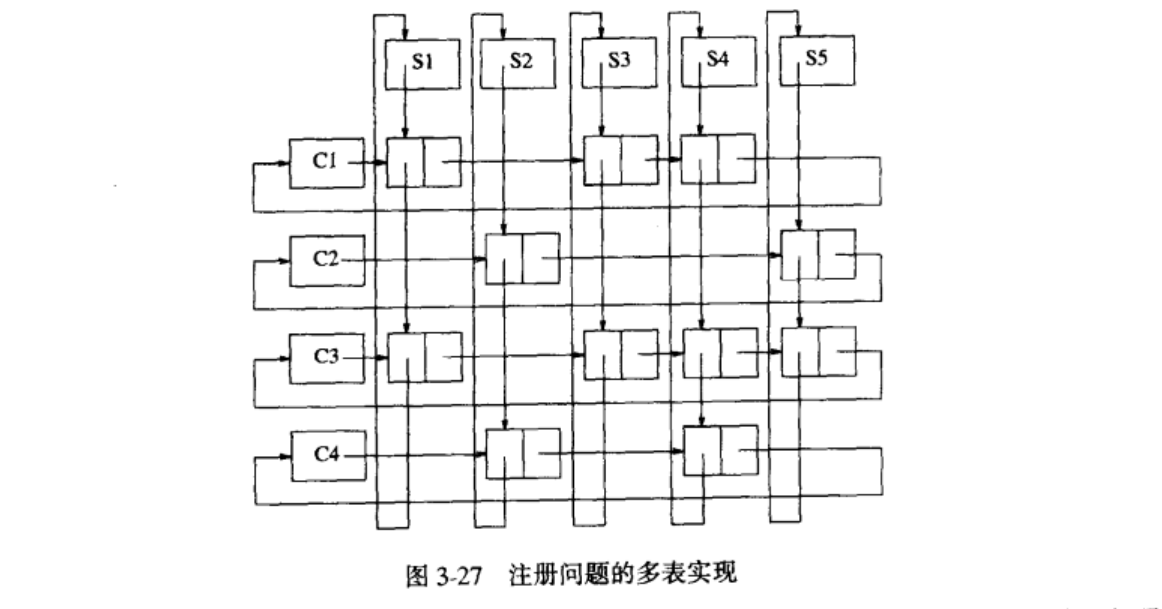
现在我们必须模拟条件2,让CursorSpace 数组中的单元代行 malloc和 free的职能。为此,我们将保留一个表(即{reelist),这个表由不在任何表中的单元构成。该表将用单元0作为表头。其初始配置如下图中表示。对于 Next,0的值等价于NULL指针。CursorSpace的初始化是一个简单的循环结构,为执行malloc 功能,将(在表头后面的)第一个元素从freelist 中删除。为了执行free功能,我们将该单元放在freelist的前端。注意,如果没有可用空间,那么我们的例程通过置P=0会正确的实现,他表示在没有空间可以用。
申请和释放空间代码如下:
//申请一块空间
static Position CursorAlloc(void){
Position P ;
P = CursorSpace[0].Next;
CursorSpace[0].Next = CursorSpace[P].Next
return P;
}
//释放一块空间
static void CursorFree(Position P) {
CursorSpace[P].Next = CursorSpace[0].Next;
CursorSpace[0].Next = p;
}
//初始化游标数组
void InitializeCursorSpace(void){
int i;
for (i = 0; i < SpaceSize - 1; i++){
CursorSpace[i].Next = i + 1;
}
CursorSpace[0].Element=0;
CursorSpace[i].Next = 0;
}
下面是游标实现链表的源代码:
cursor.h
#ifndef _Cursor_H
typedef int ElementType;
typedef int PtrToNode;
typedef PtrToNode List;
typedef PtrToNode Position;
#define SpaceSize 50
void InitializeCursorSpace(void);
List MakeEmpty(List L);
int IsEmpty(const List L);
int IsLast(const List L,const Position P);
Position Find(const List L,ElementType X);
Position FindPrevious(List L,ElementType X);
void Insert(List L,Position P,ElementType X);
void Delete(List L,ElementType X);
void DeleteList(List L);
Position Header(const List L);
Position First(const List L);
Position Advance(const Position P);
ElementType Retrieve(const Position P);
#endif
struct Node{
ElementType Element;
Position Next;
};
struct Node CursorSpace[SpaceSize];
cursor.c
#include <stdio.h>
#include "cursor.h"
//初始化游标数组
void InitializeCursorSpace(void){
int i;
for (i = 0; i < SpaceSize - 1; i++){
CursorSpace[i].Next = i + 1;
}
CursorSpace[0].Element=0;
CursorSpace[i].Next = 0;
}
//申请一块空间
static Position CursorAlloc(void){
Position P ;
P = CursorSpace[0].Next;
CursorSpace[0].Next = CursorSpace[P].Next
return P;
}
//释放一块空间
static void CursorFree(Position P) {
CursorSpace[P].Next = CursorSpace[0].Next;
CursorSpace[0].Next = p;
}
//生成一个空链表
List MakeEmpty(List L){
if (CursorSpace[L].Next != 0) {
DeleteList(L);
}
return L;
}
//判断是否为空链表
int IsEmpty(const List L){
return CursorSpace[L].Next == 0;
}
//判断是否是最后一个节点
int IsLast(const List L,const Position P){
return CursorSpace[P].Next == 0;
}
//查找含有元素X的结点(找不到P为NULL)
Position Find(const List L,ElementType X){
Position Temp = CursorSpace[L].Next;
while(Temp!=0 && CursorSpace[Temp].Element!=X){
Temp = CursorSpace[Temp].Next;
}
}
//查找含有元素X的结点的前驱元 (找不到P为最后一个元素)
Position FindPrevious(const List L,ElementType X){
Temp = CursorSpace[L].Next;
while(Temp!=0 && CursorSpace[Temp].Element!=X){
Temp = CursorSpace[Temp].Next;
}
}
//在P位置之后,插入一个元素为X的结点
void Insert(List L,Position P,ElementType X){
Position Temp = CursorAlloc();
if(Temp ==0 ){
printf("Out Of Space!!");
return;
}
CursorSpace[Temp].Element =X;
CursorSpace[Temp].Next = CursorSpace[P].Next;
CursorSpace[P].Next = Temp;
}
//删除P结点
void Delete(List L,ElementType X){
Position P = FindPrevious(L,X);
Position Temp;
if(!IsLast(L,P)){
Temp = CursorSpace[P].Next;
CursorSpace[P].Next = CursorSpace[Temp].Next;
CursorFree(Temp);
}
}
//删除链表(表头还在)
void DeleteList(List L){
Position P = CursorSpace[L].Next;
Position TempCell;
while(P!=0){
TempCell = CursorSpace[P].Next;
CursorFree(P);
P=TempCell;
}
}
//返回表头结点
Position Header(const List L){
return L;
}
//返回第一个结点
Position First(const List L){
return CursorSpace[L].Next;
}
//返回P结点的后继元
Position Advance(const Position P){
return CursorSpace[P].Next;
}
//返回P结点的元素
ElementType Retrieve(const Position P){
return CursorSpace[P].Element;
}
3.3 栈
引入:freelist 从字面上看表示一种有趣的数据结构。从freelist 删除的单元是刚刚由free 放在那里的单元。因此,最后被放在freelist的单元是被最先拿走的单元。有一种数据结构也具有这种性质,叫作栈(stack)。
3.3.2 栈模型
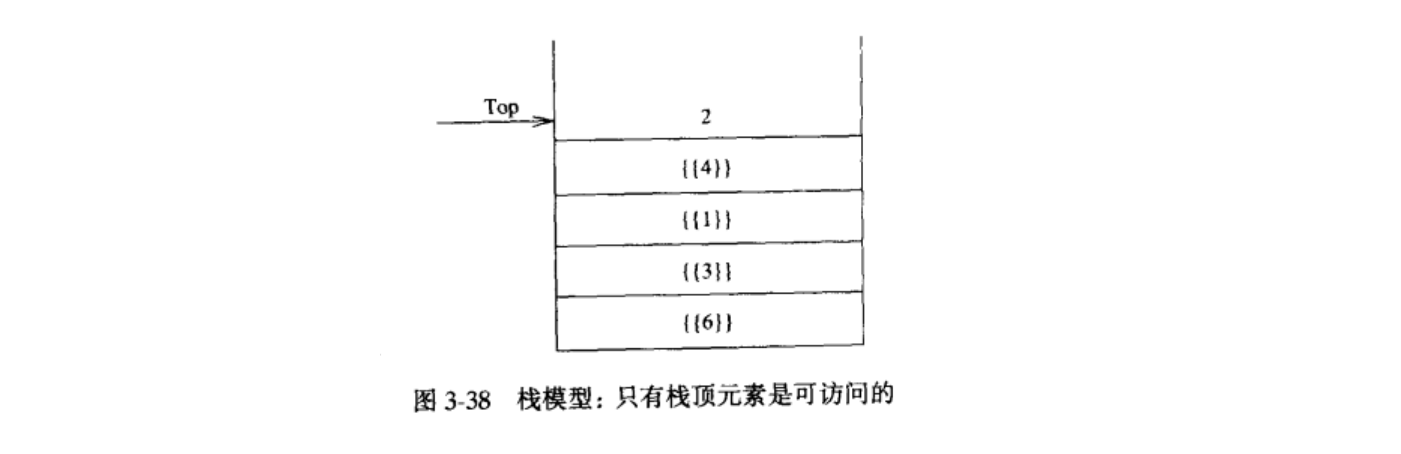
栈(stack)是限制插入和删除只能在一个位置上进行的表,该位置是表的末端,叫做栈的顶(top)。对栈的基本操作有Push(进栈)和Pop(出栈),前者相当于插入,后者则是删除最后插入的元素。最后插人的元素可以通过使用Top例程在执行Pop之前进行考查。对空栈进行的 Pop 或 Top 一般被认为是栈 ADT的错误。另一方面,当运行 Push 时空间用尽是一个实现错误,但不是 ADT错误。栈有时又叫做 LIFO(后进先出)表。
3.3.2 栈的实现
由于栈是一个表,因此任何实现表的方法都能实现栈。
1.链表实现
#ifndef _Stack_h
struct Node;
typedef struct Node *PtrToNode;
typedef PtrToNode Stack;
typedef int ElementType;
int IsEmpty(Stack S);
Stack CreateStack();
void DisposeStack(Stack S);
void MakeEmpty(Stack S);
void Push(Stack S,ElementType X);
ElementType Top(Stack S);
void Pop(Stack S);
#endif
struct Node{
ElementType Element;
PtrToNode Next;
};
#include "stack.h"
#include <stdio.h>
#include <stdlib.h>
//判断栈是否为空
int IsEmpty(Stack S){
return S->Next==NULL;
}
//创建一个空栈
Stack CreateStack(){
Stack S;
S = (Stack)malloc(sizeof(struct Node));
if(S==NULL){
printf("Error! Out Of Space!");
}
S->Next=NULL;
return S;
}
//重置栈
void DisposeStack(Stack S){
PtrToNode P,TempCell;
P = S->Next;
S->Next=NULL;
while(P){
TempCell = P->Next;
free(P);
P = TempCell;
}
free(S);
}
//使栈为空
void MakeEmpty(Stack S){
if(S==NULL){
printf("Error! Must use CreateStack first!");
}
while(!IsEmpty(S)){
Pop(S);
}
}
//进栈
void Push(Stack S,ElementType X){
PtrToNode tempCell;
tempCell = (PtrToNode)malloc(sizeof(struct Node));
if(tempCell==NULL){
printf("Error! Out Of Space!");
}else{
tempCell->Element = X;
tempCell->Next = S->Next;
S->Next=tempCell;
}
}
//栈顶元素
ElementType Top(Stack S){
if(!IsEmpty(S)){
return S->Next->Element;
}else{
printf("Error! Empty stack!!");
}
}
//出栈
void Pop(Stack S){
if(!IsEmpty(S)){
PtrToNode FirstCell = S->Next;
S->Next=FirstCell->Next;
free(FirstCell);
}else{
printf("Error! Empty stack!!");
}
}
2.数组实现
用一个数组实现栈是很简单的。每一个栈有一个TopOfStack,对于空栈它是-1(这就是空栈的初始化)。为了将某个元素X压入到该栈中,我们将TopOfStack加1,然后置Stack[TopOfStack]= X.其中 Stack是代表具体栈的数组。为了弹出栈元素,我们置返回值为 Stack[TopOfStack],然后 TopOfStack 减1。
注意,这些操作不仅以常数时间运行,而且是以非常快的常数时间运行。在某些机器上,若在带有自增和自减寻址功能的寄存器上操作,则(整数的)Push和Pop都可以写成一条机器指令。最现代化的计算机将栈操作作为它的指令系统的一部分,这个事实强化了这样一种观念,即栈很可能是在计算机科学中在数组之后最基本的数据结构。
一个影响栈的执行效率的问题是错误检测。我们的链表实现中是仔细地检查错误的。正如上面所描述的,对空栈的Pop或是对满栈的Push都将超出数组的界限并引起程序崩溃显然,我们不愿意出现这种情况。但是,如果把对这些条件的检测放到数组实现过程中,那就很可能要花费像实际栈操作那样多的时间。由于这个原因,除非在错误处理极其重要的场合(如在操作系统中),一般在栈例程中省去错误检测就成了普通的惯用手法。
#ifndef _Stack_h
struct StackRecord;
typedef struct StackRecord *Stack;
typedef int ElementType;
int IsEmpty(Stack S);
int IsFull(Stack S);
Stack CreateStack(int MaxElements);
void DisposeStack(Stack S);
void MakeEmpty(Stack S);
void Push(Stack S,Element X);
ElementType Top(Stack S);
void Pop(Stack S);
ElementType TopAndPop(Stack S);
#endif
#define EmptyTos (-1)
#define MinStackSize (5)
struct StackRecord{
int Capacity;//栈的容量
int TopOfStack;//栈头元素索引
ElementType * Array;
};
#include "stack.h"
int IsEmpty(Stack S){
return S->TopOfStack==EmptyTos;
}
void MakeEmpty(Stack S){
S->TopOfStack==EmptyTos;
}
int IsFull(Stack S){
return S->TopOfStack=S->Capacity-1;
}
Stack CreateStack(int MaxElements){
if(MaxElements<MinStackSize){
printf("Error!Stack size is too small!");
}else{
Stack S;
S = (Stack)malloc(sizeof(struct StackRecord));
if(S==NULL){
printf("Error!Out Of Space!");
}else{
S->Capacity = MaxElements;
S->Array = (ElementType*)malloc(MaxElements*sizeof(ElementType));
if(S->Array ==NULL){
printf("Error!Out Of Space!");
}else{
MakeEmpty(S);
return S;
}
}
}
}
void DisposeStack(Stack S){
if(S!=NULL){
free(S->Array);
free(S);
}
}
void Push(Stack S,Element X){
if(!IsFull(S)){
S->Array[++(S->TopOfStack)] = X;
}else{
printf("Error!Full Stack!");
}
}
ElementType Top(Stack S){
if(!IsEmpty(S)){
return S->Array[S->TopOfStack];
}else{
printf("Error!Empty Stack!");
return 0;
}
}
void Pop(Stack S){
if(!IsEmpty(S)){
S->TopOfStack--;
}else{
printf("Error!Empty Stack!");
}
}
ElementType TopAndPop(Stack S){
if(!IsEmpty(S)){
return S->Array[S->TopOfStack--];
}else{
printf("Error!Empty Stack!");
}
return 0 ;
}
3.3.3 应用
毫不奇怪,如果我们把操作限制于一个表,那么这些操作会执行得很快。然而,令人惊奇的是,这些少量的操作非常强大和重要。在栈的许多应用中,我们给出三个例子,第三个实例深刻说明程序是如何组织的。
1.平衡符号
编译器检查你的程序的语法错误,但是常常由于缺少一个符号(如遗漏一个花括号或是注释起始符)引起编译器列出上百行的诊断,而真正的错误并没有找出。
在这种情况下一个有用的工具就是检验是否每件事情都能成对出现的一个程序。于是每一个右花括号、右方括号及右圆括号必然对应其相应的左括号。序列“[()]”是合法的,但“[( ])"是错误的。显然,不值得为此编写一个大型程序,事实上检验这些事情是很容易的。为简单起见,我们仅就圆括号、方括号和花括号进行检验并忽略出现的任何其他字符。这个简单的算法用到一个栈,叙述如下:
做一个空栈。读入字符直到文件尾。
如果字符是一个开放符号,则将其推入栈中。
如果字符是一个封闭符号,则当栈空时报错。否则,将栈元素弹出。
如果弹出的符号不是对应的开放符号,则报错。
在文件尾,如果栈非空则报错。
你应该能够确信这个算法是会正确运行的。很清楚,它是线性的,事实上它只需对输入进行一趟检验。因此,它是在线(on-line)的,是相当快的。当报错时,决定如何处理需要做一些附加的工作--例如判断可能的原因。
2.1 后缀表达式求值
假设我们有一个便携计算器并想要计算一趟外出购物的花费。为此,我们将一列数据相加并将结果乘以1.06:它是所购物品的价格以及附加的地方税。如果购物各项花销为4.99.5.99,和6.99,那么输人这些数据的自然的方式将是4.99+5.99+6.99* 1.06=;随着计算器的不同,这个结果或者是所要的答案19.05,或者是科学容案18.39。
最简单的四功能计算器将给出第一个答案,但是许多先进的计算器是知道乘法的优先级是高于加法的。
另一方面,有些项是需要上税的而有些项则不是,因此,如果只有第一项和最后一项是要上税的,那么4.99* 1.06+5.99+6.99 * 1.06=将在科学计算器上给出正确的答案(18.69),而在简单计算器上给出错误的答案(19.37) 。
科学计算器一般包含括号,因此我们总可以通过加括号的方法得到正确的答案,但是使用简单计算器我们需要记住中间结果。该例的典型计算顺序可以是将4.99和1.06相乘并存为A,然后将5.99和A 相加,再将结果存人A。我们再将6.99和1.06相乘并将答案存为A2,最后将A和相Az加并将最后结果放人A。我们可以将这种操作顺序书写如下:
4.99 1.06* 5.99+6.99 1.06 * +
这个记法叫做后缀 或 逆波兰记法,其求值过程恰好就是我们上面所描述的过程。计算这个问题最容易的方法是使用一个栈。当见到一个数时就把它推入栈中;在遇到一个运算符时该算符就作用于从该栈弹出的两个数(符号)上,将所得结果推入栈中,例如,后缀表达式
6 5 2 3 + 8 * + 3 + *

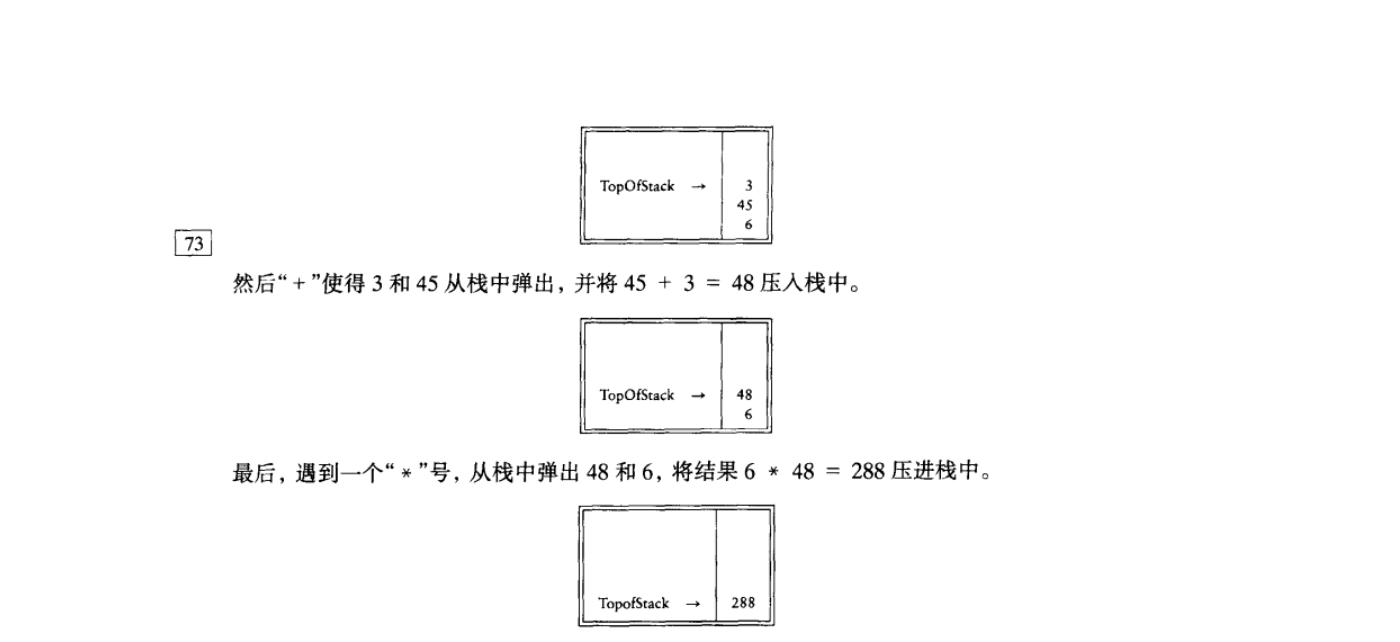
计算一个后缀表达式花费的时间是 (N),因为对输入中的每个元素的处理都是由一些栈操作组成从而花费常数时间。该算法的计算是非常简单的。注意,当一个表达式以后级记号给出时,没有必要知道任何优先规则。这是一个明显的优点。
代码实现:
bool isNumber(char* token) {
return strlen(token) > 1 || ('0' <= token[0] && token[0] <= '9');
}
int evalRPN(char** tokens, int tokensSize) {
int n = tokensSize;
int stack[n], top = 0;
for (int i = 0; i < n; i++) {
char* token = tokens[i];
if (isNumber(token)) {
stack[top++] = atoi(token);
} else {
char sign = token[0];
int m = stack[--top];
int n = stack[--top];
switch (sign) {
case '+':
stack[top++] = m + n;
break;
case '-':
stack[top++] = n - m;
break;
case '*':
stack[top++] = m * n;
break;
case '/':
stack[top++] = n / m;
break;
}
}
}
return stack[top - 1];
}
2.2中缀转后缀表达式
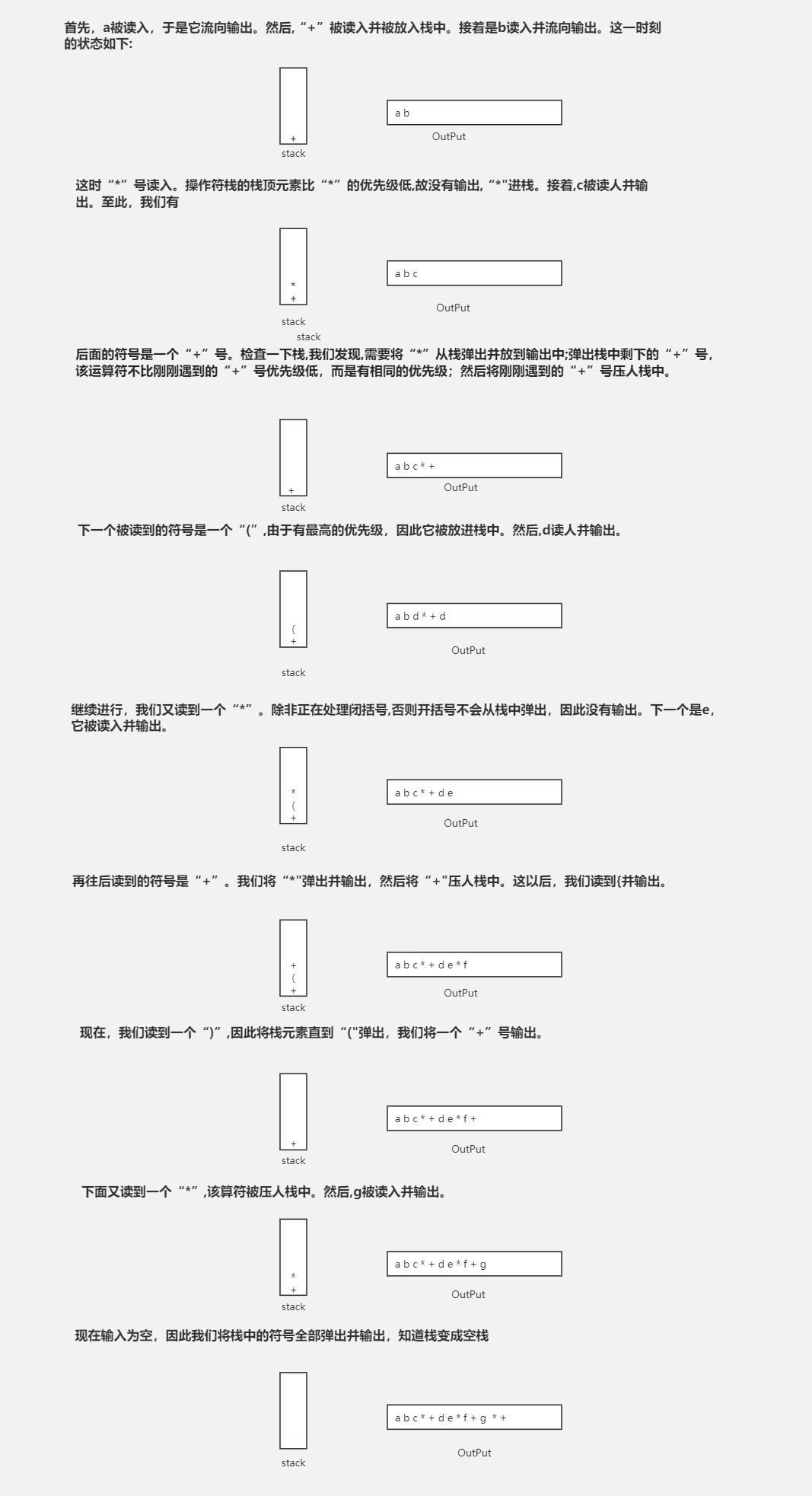
栈不仅可以用来计算后缀表达式的值,而且我们还可以用栈将一个标准形式的表达式(或叫做中缀式(infix))转换成后缀式。设我们欲将中缀表达式
a + b * c + ( d * e + f ) * g
转换成后缀表达式。正确的答案是
a b c * + d e * f + g * +
当读到一个操作数的时候,立即把它放到输出中。操作符不立即输出,从而必须先存在某个地方。正确的做法是将已经见到过的操作符放进栈中而不是放到输出中。当遇到左圆括号时我们也要将其推入栈中。我们从一个空栈开始计算。
如果见到一个右括号,那么就将栈元素弹出,将弹出的符号写出直到我们遇到一个(对
应的)左括号,但是这个左括号只被弹出,并不输出。如果我们见到任何其他的符号(“+”,“*”,“(”),那么我们从栈中弹出栈元素直到发现优先级更低的元素为止。有一个例外:除非是在处理一个“)”的时候,否则我们绝不从栈中移走“(”。对于这种操作,“+”的优先级最低,而“(”的优先级最高。当从栈弹出元素的工作完成后,我们再将操作符压人栈中。
最后,如果我们读到输人的末尾,我们将栈元素弹出直到该栈变成空栈,将符号写到输出中。
为了理解这种算法的运行机制,我们将把上面的中缀表达式转换成后缀形式。
代码实现:
#include <stdio.h>
#include <stdlib.h>
//#include "stack.h"
#include <string.h>
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
int isNumber(char* C);
void infixToPostfix(char** tokens, int infixSize,char** postfix);
int precedence(char sign);
char* charToString(char c);
int main(int argc, char *argv[]) {
char* infix [] = {"12","+","3","*","67","+","(","78","*","78","+","5",")","*","6"};
int infixSize = sizeof(infix)/sizeof(char*);
printf("前缀表达式:");
int i;
for(i = 0; i < infixSize; i++){
if(i == infixSize - 1){
printf("%s\n", infix[i]);
} else {
printf("%s ", infix[i]);
}
}
char** postfix = (char**)malloc(infixSize * sizeof(char*));
infixToPostfix(infix,infixSize,postfix);
printf("后缀表达式:");//这里-2是减去两个中括号
for(i = 0; i < infixSize - 2; i++){
if(i == infixSize - 1){
printf("%s\n", postfix[i]);
} else {
printf("%s ", postfix[i]);
}
}
}
//获取优先级
int precedence(char sign){
switch(sign){
case '+':
case '-':
return 1;
break;
case '*':
case '/':
return 2;
break;
case '(':
case ')':
return 0;
break;
}
}
//判断C是否为数组
int isNumber(char* C){
return strlen(C)>1 || C[0]>='0' && C[0]<='9';
}
//中缀转后缀表达式
void infixToPostfix(char** tokens, int infixSize,char** postfix) {
//栈 用于存放符号
char stack[infixSize],top = 0;
//输出数组的最右边
int postfixTop = 0;
int i;
for(i=0;i<infixSize;i++){
char* token = tokens[i];
if(isNumber(token)){
postfix[postfixTop++] = token;
}else{
char sign = token[0];
//如果栈为空,或者新加的符号优先级比栈顶元素的优先级高,那么直接把符号放入
if(top==0 || sign == '(' || precedence(sign) > precedence(stack[top-1])){
stack[top++] = sign;
//如果新加的符号是)那么栈一直弹出元素直到碰见(
}else if(sign == ')'){
while(stack[top-1]!='('){
char temp = stack[--top];
postfix[postfixTop++] = charToString(temp);
}
top--;
//如果新加的符号是优先级没有栈顶符号高,那么栈一直弹出元素
}else{
while(top>=0 && precedence(sign) <= precedence(stack[top-1])){
char temp = stack[--top];
postfix[postfixTop++] = charToString(temp);
}
stack[top++] = sign;
}
}
}
//将剩余在栈中的符号弹出
while(top>0){
char temp = stack[--top];
postfix[postfixTop++] = charToString(temp);
}
return postfix;
}
//字符转字符串
char* charToString(char c){
char* array = (char*)malloc(2 * sizeof(char));
array[0] = c;
array[1] = '\0';
return array;
}
3.函数调用
检测平衡符号的算法提供一种实现函数调用的方法。这里的问题是,当调用一个新函数时,主调例程的所有局部变量需要由系统存储起来,否则被调用的新函数将会覆盖调用例程的变量。不仅如此,该主调例程的当前位置必须要存储,以便在新函数运行完后知道向哪里转移。这些变量一般由编译器指派给机器的寄存器,但存在某些冲突(通常所有的过程都将某些变量指派给1#寄存器),特别是涉及递归的时候。该问题类似于平衡符号的原因在于函数调用和函数返回基本上类似于开括号和闭括号,二者想法是一样的。
当存在函数调用的时候,需要存储的所有重要信息,诸如寄存器的值(对应变量的名字)和返回地址(它可从程序计数器得到,典型情况下计数器就是一个寄存器)等,都要以抽象的方式存在“一张纸上”并被置于一个堆(pile)的顶部。然后控制转移到新函数,该函数自由地用它的一些值代替这些寄存器。如果它又进行其他的函数调用,那么它也遵循相同的过程。当该函数要返回时,它査看堆(pile)顶部的那张“纸"并复原所有的寄存器。然后它进行返回
转移。显然,所有全部工作均可由一个栈来完成,而这正是在实现递归的每一种程序设计语言中实际发生的事实。 所存储的信息或称为活动记录(activationrecord),或叫做栈帧(stackframe)。在典型情况下,需要做些微调整:当前环境是由栈顶描述的。因此,一条返回语句就可给出前面的环境(不用复制)。在实际计算机中的栈常常是从内存分区的高端向下增长,而在许多的系统中是不检测溢出的。由于有太多的同时在运行着的函数,用尽栈空间的情况总是可能发生的。显而易见,用尽栈空间常是致命的错误。
3.4 队列
像栈一样,队列(queue)也是表。然而,使用队列时插人在一端进行而删除则在另一端进行。
3.4.1 队列模型
队列的基本操作是 Enqueue(入队),它是在表的末端(叫做队尾(rear))插入一个元素,还有 Dequeue(出队),它是删除(或返回)在表的开头(叫做队头(front))的元素。图 3-56显示一个队列的抽象模型。

3.4.2 队列的数组实现
如同栈的情形一样,对于队列而言任何表的实现都是合法的。像栈一样,对于每一种操作,链表实现和数组实现都给出快速的(1)运行时间。下面演示数组模拟环形队列实现。
#ifndef _Queue_h
struct QueueRecord;
typedef struct QueueRecord *Queue;
typedef int ElementType;
int IsEmpty(Queue Q);
int IsFull(Queue Q);
Queue CreateQueue(int MaxElements);
void DisposeQueue(Queue Q);
void MakeEmpty(Queue Q);
void Enqueue(Queue Q,ElementType X);
ElementType Front(Queue Q);
void Dequeue(Queue Q);
ElementType FrontAndDequeue(Queue Q);
#endif
# define MiQueueSize (5)
struct QueueRecord{
int Capacity;
int Front; //指向第一个元素
int Rear; //指向最后一个元素的后一个位置
ElementType *Array;
};
#include <stdio.h>
#include <stdlib.h>
#include "queue.h"
int IsEmpty(Queue Q){
return Q->Front == Q->Rear;
}
//为了区分数组为空或者队列满的两种情况,我们认定当当有maxSize-1个元素的时候,队列为满。
int IsFull(Queue Q){
return (Q->Rear+1) % Q->Capacity == Q->Front;
}
Queue CreateQueue(int MaxElements){
Queue Q = (Queue)malloc(sizeof(struct QueueRecord));
if(Q==NULL){
printf("Out Of Space!");
exit(1);
}
Q->Front= 0;
Q->Rear = 0;
Q->Capacity = MaxElements;
Q->Array = (ElementType*)malloc(MaxElements * sizeof(ElementType));
if(Q->Array==NULL){
printf("Out Of Space!");
exit(1);
}
return Q;
}
void DisposeQueue(Queue Q){
free(Q);
Q = NULL;
}
void MakeEmpty(Queue Q){
Q->Front= 0;
Q->Rear = 0;
}
void Enqueue(Queue Q,ElementType X){
if(IsFull(Q)) {
printf("Full Queue!");
exit(1);
}else{
Q->Array[Q->Rear] = X;
Q->Rear= (Q->Rear+1)% Q->Capacity;
}
ElementType Front(Queue Q){
if(IsEmpty(Q)){
printf("Empty Queue!!");
exit(1);
}
return Q->Array[Q->Front];
}
void Dequeue(Queue Q){
if(IsEmpty(Q)) {
printf("Empty Queue!");
exit(1);
}else{
Q->Front = (Q->Front+1)%Q->Capacity;
}
}
ElementType FrontAndDequeue(Queue Q){
if(IsEmpty(Q)) {
printf("Empty Queue!");
exit(1);
}else{
ElementType X = Q->Array[Q->Front];
Q->Front= (Q->Front+1)%Q->Capacity;
return X;
}
}
3.4.3 队列的应用
有几种使用队列给出提高运行效率的算法。它们当中有些可以在图论中找到,我们将在第9章讨论它们。这里,先给出某些应用队列的例子。
- 当作业送交给一台行式打印机,它们就按照到达的顺序被排列起来。因此,被送往行式打印机的作业基本上是被放到一个队列中。
实际生活中的每次排队都(应该)是一个队列。例如,在一些售票口排列的队都是队列。因为服务的顺序是先来到的先买票。 - 另一个例子是关于计算机网络的。有许多种PC机的网络设置,其中磁盘是放在一台叫做文件服务器的机器上的。使用其他计算机的用户是按照先到先使用的原则访问文件的,因此其数据结构是一个队列。
- 进一步的例子如下:
当所有的接线员忙得不可开交的时候,对大公司的传呼一般都被放到一个队列中在大规模的大学里,如果所有的终端都被占用,由于资源有限,学生们必须在一个等待表上签字。在终端上呆得时间最长的学生将首先被强制离开,而等待时间最长的学生则将是下一个被允许使用终端的用户。处理用概率的方法计算用户排队预计等待时间、等待服务的队列能够排多长,以及其他些诸如此类的问题将用到被称为排队论(queueingtheory)的整个数学分支。
问题的答案依赖于用户加入队列的频率以及一旦用户得到服务时处理服务花费的时间。这两个参数作为概率分布函数给出。在一些简单的情况下,答案可以解析算出。一种简单的例子是一条电话线有一个接线员。如果接线员忙,打来的电话就被放到一个等待队列中(这还与某个容许的最大限度有关)。这个问题在商业上很重要,因为研究表明,人们会很快挂上电话。
如果我们有k个接线员,那么这个问题解决起来要困难得多。解析求解困难的问题往往使用模拟的方法求解。此时,我们需要使用一个队列来进行模拟。如果k很大,那么我们还需要其他一些数据结构来使得模拟更有效地进行。在第6章将会看到模拟是如何进行的。那时我们将对k的若干值进行模拟并选择能够给出合理等待时间的最小的k。正如栈一样,队列还有其他丰富的用途,这样一种简单的数据结构竟然能够如此重要实在令人惊奇。




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步