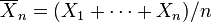(二)概率论之随机变量
1. 什么是随机变量?
在(一)中已经介绍 样本空间$\Omega$和基本事件$\omega$,若对任意$\omega$有唯一$X(\omega) \in R$,我们则称$X$为随机变量(取值函数)。注意$\{\omega|X(\omega)=x\}\subset \Omega $,一般简写
\[P(\{\omega|X(\omega)=x\})=P(X=x)\]
有时我们不仅要知道$P(X=x)$的值,也需要知道$P(a\leq X \leq b)$和$P(X\leq x)$,$P(X \geq x)$的值。根据事件之间的运算和柯尔莫哥洛夫三公理,我们选取
\[F(x)=P(X\leq x)\]
作为我们研究的对象,称$F(x)$为分布函数(acmulative distribution function)。当然也可以定义其他类型的“分布函数”,。关于随机变量的研究是概率论的中心内容。我们这样定义的分布函数有下面的性质:
(i) $F(-\infty)=0,F(+\infty)=1$
(ii) $F(x)$是单调递增的
(iii) 分析$F(x)$的连续性和可微性已经涉及到极限运算
根据随机变量的取值类型,随机变量可以分为离散型随机变量和连续型随机变量。有了分布函数,关于概率的所有问题都可以解决了。对离散型随机变量称$P(X=x)$为概率质量函数。比较常见的有
(1) 二项分布
抛硬币实验,假设硬币材质均匀,抛$n$次,有$k$次都是正面朝上,这个事件的概率是多大呢?这是古典概率的东西,无非是排列组合。
\[P(X=k)=C_{n}^{k}(\frac{1}{2})^{n-k}(\frac{1}{2})^{k}\]
当硬币材质非均匀时,设朝上的概率为$p$,并记朝上为成功事件则
\[P(X=k)=C_{n}^{k}p^{k}(1-p)^{n-k}\]
我们能算出上述$k$取多少时,概率达到最大。有了上面的概率质量函数,分布函数是容易求出的无非是有限项的和。
引入极限,当$n \to \infty$时,我们需要一些近似估计便于计算。日后再表。另一种极限就是$p$很小时的估计。
二项分布$b(n,p)$及其重要,它和$Possion$分布以及大名鼎鼎的$Gauss$分布都存在血缘关系,可以算作他们的Father. 概率论发源早期也着重在
(2) 几何分布
进行一项独立实验例如抛硬币,直至出现正面事件成功概率为$p$,结束实验,问在第$k$次实验成功的概率是多少?
\[P(X=k)=(1-p)^{k-1}p\]
(3) Possion分布
一段时间内,某交通路口所发生的交通事故的个数?
解决这个问题的基本思路是这样的,将时间$[0, 1]$划分$n$段,$n$足够大以至于在这么短暂的时间内只能发生一次事故,发生事故的概率与时间长成正比$\frac{\lambda}{n}$。$k$起事故服从二项分布,概率为
\[P(x=k)=C_{n}^{k}(\frac{\lambda}{n})^{k}(1-\frac{\lambda}{n})^{n-k}\]
令$n \to \infty$得到
\[P(X=k)=e^{-\lambda}\frac{\lambda^{k}}{k!}\]
上述分布称为$Possion$分布,从上可看出$p=n\lambda$,$n$很大时$p$很小,当$p \leq 0.003$时称为小概率事件,$\lambda$具有统计学意义“均值”。
下面介绍常见的连续型随机变量的分布:
首先引入概率密度函数$f(x)$,概率密度函数是累积分布函数$F(x)$的导数,有下面的三条性质:
(i) $f(x)\geq 0$
(ii) $\int_{-\infty}^{+\infty}f(x)dx=1$
(iii)$P(a\leq x \leq b)=F(b)-F(a)=\int_{-\infty}^{+\infty}f(x)dx$
反而言之,只要满足性质(i)、(ii)、(iii)的都可以作为概率密度函数,此时$F(x)=\int_{-\infty}^{x}f(x)dx$.$f(x)dx$表示随机变量取值$[x,x+\Delta x]$的概率。
(4) Gauss 正态分布
这个分布是所有分布里最重要的分布
\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma ^{2}}}\]
关于这个分布的来源很多教课书没有作太多的介绍,她是和误差估计、最小二乘法、中心极限定理等相关的,网络上有一篇非常著名的文章《关于正态分布的前世今生》作了详细介绍,非常精彩。
当$\mu=0,\sigma=1$时
\[f(x)=\frac{1}{\sqrt{2\pi}}e^{-x^2}\]
若随机变量$X$服从正态分布,则记为$X \sim N(\mu,\sigma ^2)$.
(5) 指数分布
\[f(x)=\lambda e^{-\lambda x},x>0\]
其他情况$f(x)=0$.
(6) 均匀分布
\[f(x)=\frac{1}{b-a},x\in [a,b]\]
其他情况$f(x)=0$.
类似可以从数学上定义其他的概率密度函数。如果只是从数学上定义了一个概率密度函数,在实际中没有应用是没有意义的。
2. 由随机变量导出新的随机变量
\[Y=g(X)\]
其中$g(x)$为给定的函数,目前为止我们可以讨论$Y$随机变量的分布
\[P(Y\leq y)=P(g(X)\leq y)=P(\omega|\omega \in A)\]
$A$指事件$g(X)\leq y$成立。
3. 上面只是讨论了一维的随机向量的分布函数,对于$\Omega_{1} \times \Omega_{2}$样本空间,我们对二维随机变量感兴趣。定义联合概率密度分布函数(jiont cumulative probability distribution function)为
\[F(x,y)=P(X\leq x,Y\leq y)\]
边缘条件分布为
\[F(x)=\sum_{y}P(X\leq x,Y\leq y)\]
\[F(y)=\sum_{x}P(X\leq x,Y\leq y)\]
对于二维连续的随机变量可以定义概率密度函数$f(x,y)$
\[F(x,y)=P(X\leq x,Y\leq y)=\int_{-\infty}^{x}\int_{-\infty}^{y}f(x,y)dxdy\]
此时,随机变量$X$和随机变量$Y$的概率密度函数分别为
\[f_{X}(x)=\int_{-\infty}^{+\infty}f(x,y)dy\]
\[f_{Y}(y)=\int_{-\infty}^{+\infty}f(x,y)dx\]
4. 我们在2中引出了可以由随机变量导出新的随机变量,关于新的随机变量讨论是不充分的,对于二维随机变量导出的新随机变量$Z=g(X,Y)$,随机变量 $Z$服从什么分布?
(1) 设随机变量$Z=X+Y$,则
\begin{align*} P(Z\leq z)&=\int \int_{\{(x,y)|x+y\leq z\}}f(x,y)dxdy\\ &=\int_{-\infty}^{+\infty}\int_{-\infty}^{z-x}f(x,y)dydx \end{align*}
所以
\[f_{Z}(z)=\frac{d }{dz}P(Z\leq z)=\int_{-\infty}^{+\infty}f(x,z-x)dx\]
上式遇到了交换次序问题要验证一致收敛条件。
若$X,Y$相互独立
则从上式易得
\[f_{Z}(z)=f(x) \ast g(x)\]
问题: 若$X,Y$分别服从参数为$N(\mu_{1},\sigma^{2})$和$N(\mu_{2},\sigma^{2})$,其和$X+Y$的分布如何?
依据上面的公式,计算可能复杂一点但是没什么实质性难度
\[f_{Z}(z)=f(x) \ast g(x)=\frac{1}{\sqrt{2\pi (\sigma_{1}^{2}+\sigma_{2}^{2})}}\exp\{-\frac{(x-\mu_1-\mu_2)^{2}}{2(\sigma_{1}^{2}+\sigma_{2}^2)}\}\]
从上面的结论可以看出$Z \sim N(\mu_{1}+\mu_{2},\sigma_{1}^{2}+\sigma_{2}^{2})$.由此这个结论可以自然推广。
这个问题并不是最有意思的,有意思的是若$Z=X+Y$服从正态分布,则$X,Y$也必定服从正态分布,这个结论着实令人震惊。这也是正态分布令人着迷的一点。这个性质称为正态分布的再生性。
(2) 随机变量商$Z=\frac{X}{Y}$的密度函数
\[P(Z\leq z)=\int_{-\infty}^{+\infty}\int_{-\infty}^{zy}f(x,y)dxdy \]
所以
\[f_{Z}(z)=\frac{d}{dz}P(Z\leq z)=\int_{-\infty}^{+\infty}yf(zy,y)dy\]
此处有误!
(3) 有了上面的准备知识就可以导出注明的“统计学上的三大分布”:$\chi^{2}$分布,$t$分布,$F$分布。这三个分布统计学里三大牛提出,在应用学科有广泛应用。
被称为服从自由度为k的卡方分布,记作
卡方分布的概率密度函数为:
为样本均值。
为样本方差。
它显示了数量
呈正态分布并且均值和方差分别为0和1。另一个相关数量
T的概率密度函数是:
 等于n − 1。 T的分布称为t-分布。参数
等于n − 1。 T的分布称为t-分布。参数 一般被称为自由度。
一般被称为自由度。

 、……、
、……、 是相互独立,符合
是相互独立,符合

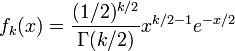
 是呈
是呈 ,
,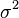 )。 令:
)。 令: