【LeetCode】线段树 segment-tree（共9题）+ 树状数组 binary-indexed-tree（共5题）

第一部分---线段树：https://leetcode.com/tag/segment-tree/  

【218】The Skyline Problem 

【307】Range Sum Query - Mutable 

【308】Range Sum Query 2D - Mutable 

【315】Count of Smaller Numbers After Self 

【493】Reverse Pairs 

【699】Falling Squares （我的线段树第一题，2019年1月24日）

在 X 轴上落方块，问最后整个区间内的最高的高度是多少。 

Input: [[1, 2], [2, 3], [6, 1]]
Output: [2, 5, 5]
Explanation:

After the first drop of positions[0] = [1, 2]:
_aa
_aa
-------
The maximum height of any square is 2.


After the second drop of positions[1] = [2, 3]:
__aaa
__aaa
__aaa
_aa__
_aa__
--------------
The maximum height of any square is 5.  
The larger square stays on top of the smaller square despite where its center
of gravity is, because squares are infinitely sticky on their bottom edge.


After the third drop of positions[1] = [6, 1]:
__aaa
__aaa
__aaa
_aa
_aa___a
--------------
The maximum height of any square is still 5.

Thus, we return an answer of [2, 5, 5].

题解：用了线段树的单点更新，只能beats 1.9% == 如果用区间更新的话， 应该快很多。但是这是第一题线段树，纪念一下。（我的线段树写的都是 base 0）

class Solution {
public:
    const static int MAX_SIZE = 1 << 15;
    struct SegmentTree {
        void init(int _n) {
            n = 1;
            while (n < _n) {
                n *= 2;
            }
            for (int i = 0; i < n * 2 -1; ++i) { dat[i] = 0; }
        }  
        #define lson(k) k*2+1
        #define rson(k) k*2+2
        #define father(k) (k-1)/2
        inline void pushup(int k) { dat[k] = max(dat[lson(k)], dat[rson(k)]); }
        void update(int k, int value) {
            k += n - 1;
            dat[k] = value;
            while (k > 0) {
                k = (k-1)/2;
                pushup(k);
            }
        }
        int query(int a, int b, int k, int l, int r) {
            if (r <= a || b <= l) { return 0; }
            if (a <= l && r <= b) {
                return dat[k];
            } else {
                int vl = query(a, b, lson(k), l, (l+r)/2);
                int vr = query(a, b, rson(k), (l+r)/2, r);
                return max(vl, vr);
            }
        }
        void print() {
            for (int i = 0; i < 2 * n - 1; ++i) {
                printf("%d ", dat[i]);
            }
            printf("\n");
        }
        int n, dat[MAX_SIZE];
    };
    vector<int> fallingSquares(vector<pair<int, int>>& positions) {
        int size = positions.size();
        set<int> st;
        for (auto pos : positions) {
            st.insert(pos.first), 
            st.insert(pos.first + pos.second - 1);
        }
        vector<int> nums(st.begin(), st.end());
        SegmentTree seg;
        seg.init((int)st.size());
        vector<int> ans;
        for (auto pos : positions) {
            int l = pos.first, r = pos.first + pos.second - 1, h = pos.second;
            int idxL = distance(st.begin(), st.find(l)), idxR = distance(st.begin(), st.find(r));
            int base = seg.query(idxL, idxR+1, 0, 0, seg.n);
            for (int i = idxL; i <= idxR; ++i) {
                seg.update(i, base + h);
            }
            int maxx = seg.query(0, (int)st.size(), 0, 0, seg.n);
            ans.push_back(maxx);
        }
        return ans;
    }
};

  

【715】Range Module 

【732】My Calendar III 

 

【850】Rectangle Area II （2019年3月15日，google tag）重叠矩形求面积

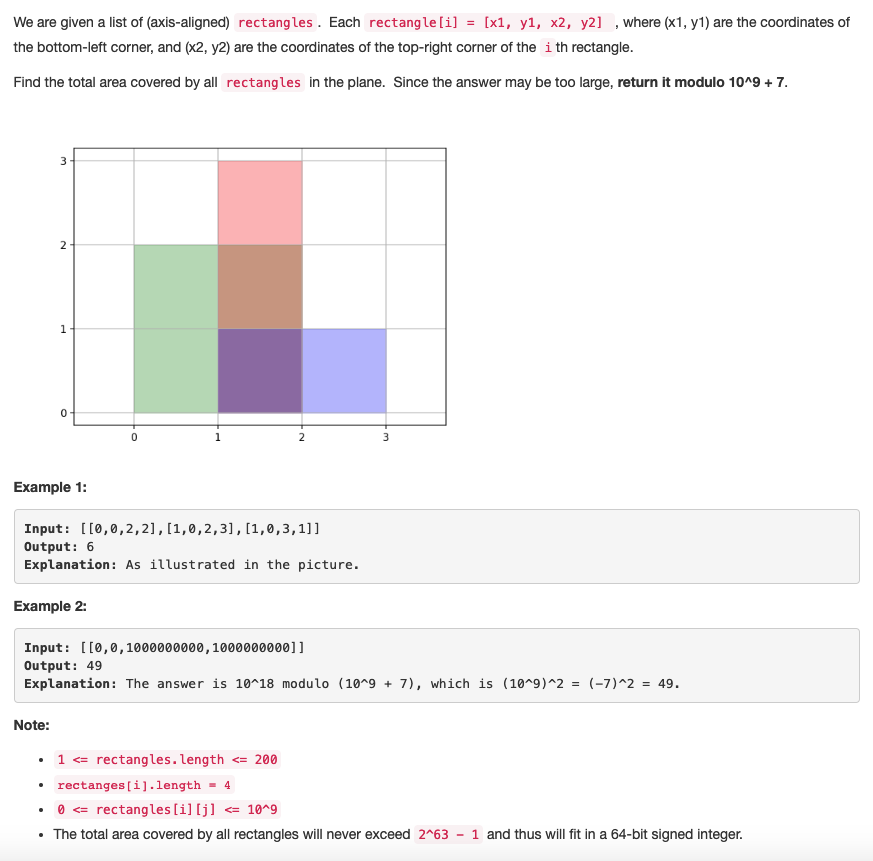
题解：我们需要一个新的grid，然后去标记grid上的每个格子是不是被矩形覆盖。grid可以不均匀，（离散化思想）。具体来说，将所有的X坐标集中起来（要去除重复），将所有的Y坐标集中起来，然后将其两两配对组成一个二维的网络。

然后对于每一个矩形，去grid上标记grid上的方格是不是被覆盖，被覆盖的话标记为 true，这个小方格需要计算面积。简单来说：在这个网络中找到每个矩形所框起来的范围（遵循左闭右开的原则），标记这个范围内的网格点为true，意味着这些网格点是落在被cover的面积里。遍历完所有的矩形后，所有标记为true的网格点都是要被算入面积的，而那些没有标记的说明不用被计算。

然后把 grid 上标记为 true 的小方格的面积加起来就可以了。

class Solution {
public:
    int rectangleArea(vector<vector<int>>& rectangles) {
        set<int> x_axis, y_axis;
        for (auto& r : rectangles) {
            x_axis.insert(r[0]),
            x_axis.insert(r[2]),
            y_axis.insert(r[1]),
            y_axis.insert(r[3]);
        }
        vector<int> x(x_axis.begin(), x_axis.end()), y(y_axis.begin(), y_axis.end());
        vector<vector<int>> grid(y.size(), vector<int>(x.size(), 0));
        for (auto& r : rectangles) {
            int xleft = distance(x_axis.begin(), x_axis.lower_bound(r[0]));
            int xright = distance(x_axis.begin(), x_axis.lower_bound(r[2]));
            int ybuttom = distance(y_axis.begin(), y_axis.lower_bound(r[1]));
            int ytop = distance(y_axis.begin(), y_axis.lower_bound(r[3]));
            for (int x0 = xleft; x0 < xright; ++x0) {
                for (int y0 = ybuttom; y0 < ytop; ++y0) {
                    grid[y0][x0] = 1;
                }
            } 
        }
        long res = 0;
        const int mod = 1e9+7;
        for (int y0 = 0; y0 < grid.size(); ++y0) {
            for (int x0 = 0; x0 < grid[y0].size(); ++x0) {
                if (grid[y0][x0]) {
                    res += long(x[x0+1] - x[x0]) * long(y[y0+1] - y[y0]);
                    res %= mod;
                }
            }
        }
        return res;
    }
};

 

第二部分---树状数组：https://leetcode.com/tag/binary-indexed-tree/

【218】The Skyline Problem (2019年1月22日)

本题想不出来用树状数组怎么做，最后自己yy出来了一种写法来做。

给了一堆大楼，给了每个楼的坐标和高度，用 (l, r, h) 表示，返回所有的 key points， A key point is the left endpoint of a horizontal line segment. 

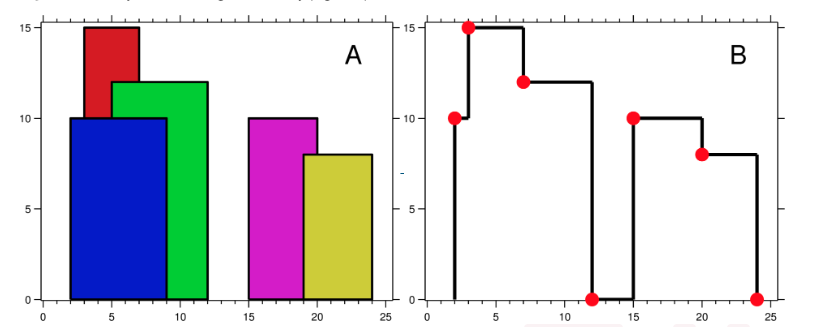
For instance, the dimensions of all buildings in Figure A are recorded as: [ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] .

For instance, the skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].

题解：这个题用BIT我是想不出来有什么解法，但是 heap （斜堆） 和 线段树可以做。我是利用了 C++ STL 里面的 multiset 做的。

我们先用扫描线看这个图，从左往右扫，如果扫描到了一个building的左边，说明这个大楼开始了，我们想查看下这个楼的左上角能不能作为 key point，如果能，就把它加到答案里面，如果不能就不加。怎么判断这个楼的左上角能不能加到答案里面呢？我们先看下它的高度，如果它比前面所有的楼都高，那它的左上角肯定是个 key point， 如果前面有比它高的楼并且这个楼还没有结束，那么他就不是一个 key point。如果扫描到了一个大楼的右边，说明这个楼结束了，那么这个楼的右边界的坐标能不能做 key point 呢？如果它前面有楼比它高，就不能，如果前面有楼跟它一样高，还是不能，只有把它删除之后，剩下所有的楼都比它矮，它才能做 key point。所以我们用扫描线依次扫描所有的坐标，就能生成答案。

//本题还有个边界情况是两个楼高度一样，如果不交叠，刚好碰上了怎么办，[[0,2,3],[2,5,3]]
class Solution {
public:
    struct kcmp {
        bool operator() (const pair<int, int>& p1, const pair<int, int>& p2) const {
            if (p1.first == p2.first) {
                return p1.second > p2.second;
            } 
            return p1.first < p2.first;
        }
    };
    vector<pair<int, int>> getSkyline(vector<vector<int>>& buildings) {
        for (auto b : buildings) {
            record.insert(make_pair(b[0], b[2]));
            record.insert(make_pair(b[1], -b[2]));//离开用负数来记录
        }
        vector<pair<int, int>> ret;
        for (auto line : record) {
            bool enter = line.second > 0 ? true : false;
            int h = abs(line.second);
            if (enter) { //如果这条线上有个楼进来了
                if (h > getMaxHeight()) {
                    ret.push_back(make_pair(line.first, h));
                }
                stHeight.insert(h);
            } else { //如果这条线有个楼出去了，可能会往ret里面加个低的点，或者前面还有楼比它高的话，就把这条线给扔了
                auto iter = stHeight.find(h);
                stHeight.erase(iter);
                if (h > getMaxHeight()) {
                    ret.push_back(make_pair(line.first, getMaxHeight()));
                }
            }
        }
        return ret;
    }
    multiset<pair<int, int>, kcmp> record; 
    multiset<int> stHeight;
    int getMaxHeight() {
        if (stHeight.empty()) {
            return 0;
        }
        return *stHeight.rbegin();
    }
};

 

【307】Range Sum Query - Mutable （2019年1月14日，学习BIT）

实现一个一维的树状数组模板。

class NumArray {
public:
    NumArray(vector<int> nums) {
        n = nums.size();
        this->nums.resize(n+1);
        bit.resize(n+1);
        for (int i = 1; i <= n; ++i) {
            this->nums[i] = nums[i-1];
            add(i, this->nums[i]);
        }      
    }
    void update(int i, int val) {
        add(i+1, val - nums[i+1]);
        nums[i + 1] = val;   
    }
    int sumRange(int i, int j) {
        ++i, ++j;
        return sum(j) - sum(i-1);
    }
    int lowbit(int x) {
        return x & -x;
    }
    void add(int x, int v) {
        for (int i = x; i <= n; i += lowbit(i)) {
            bit[i] += v;
        }
    }
    int sum(int x) {
        int ret = 0;
        for (int i = x; i > 0; i -= lowbit(i)) {
            ret += bit[i];
        }
        return ret;
    }
    vector<int> nums, bit;
    int n;
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * obj.update(i,val);
 * int param_2 = obj.sumRange(i,j);
 */

 

【308】Range Sum Query 2D - Mutable （2019年1月14日，学习BIT）

 

【315】Count of Smaller Numbers After Self (2019年1月22日，Fenwick Tree 练习)

给了一个数组 nums， 返回一个数组，数组中的元素 ret[i] 代表 nums[i] 的右边有多少个比它小的数。（题目如果换一下， 求每个元素左/右边有多少个比它小/大/大于等于/小于等于的数）

You are given an integer array nums and you have to return a new counts array. The counts array has the property where counts[i] is the number of smaller elements to the right of nums[i].

Example:
Input: [5,2,6,1]
Output: [2,1,1,0] 
Explanation:
To the right of 5 there are 2 smaller elements (2 and 1).
To the right of 2 there is only 1 smaller element (1).
To the right of 6 there is 1 smaller element (1).
To the right of 1 there is 0 smaller element.

题解：这个题第一个想法是dp做，但是尝试了两下，完全推导不了。dp做不出来。看了下tag是树状数组，还有BST等等等很多种解法。我这次先练习下怎么用树状数组解题。

树状数组有两个用途（1）用 O(logN)的时间求前缀和。（2）用log(N)的时间在位置为 i 的元素上增加一个数。

这个题求数组中一个元素右边有多少个数比它小。我们如果翻转下数组，就可以变成求数组中一个元素左边有多少元素比它小。

那么它和 Fenwick Tree 有什么关系呢？

你想啊，我们可以把原数组先排序并且去重，得到一个递增的并且unique元素的新数组，但是呢这个新数组不能代表原来的数组，因为原来数组中可能有重复元素。所以我们搞出来一个 freq 数组(其实就是我们树状数组的原来数组)，配合sorted数组使用。

sorted数组里面的元素不是连续的，我们需要把它离散化，求出他们的相对位置。关系如下图：

nums:      [7, 1, 3, 2, 9, 2, 1]

sorted:    [1, 2, 3, 7, 9] （1-based）（其实就是我们元素 对应 树状数组的下标） sorted[nums[i]] = j

reversed: [1, 2, 9, 2, 3, 1, 7]

rank:       [1, 2, 5, 2, 3, 1, 4]

依次遍历 reversed 数组，先求这个元素前面有多少个元素小于它(树状数组的前缀和)，增加每个元素的 freq。往下求就ok了。

class Solution {
public:
    class FenwickTree {
    public:
        FenwickTree(int n): sums_(n+1, 0) {}
        void add (int i, int delta) {
            while (i < sums_.size()) {
                sums_[i] += delta;
                i += lowbit(i);
            }
        }
        int query (int i) {
            int sum = 0;
            while (i > 0) {
                sum += sums_[i];
                i -= lowbit(i);
            }
            return sum;
        }
    private:
        static inline int lowbit(int x) {return x & -x;}
        vector<int> sums_;
    };
    vector<int> countSmaller(vector<int>& nums) {
        set<int> sorted(nums.begin(), nums.end());
        unordered_map<int, int> rank;
        int r = 0;
        for (auto num : sorted) {
            rank[num] = ++r;
        }
        vector<int> ret;
        FenwickTree bit(rank.size());
        for (int i = nums.size() - 1; i >= 0; --i) {
            r = rank[nums[i]];
            ret.push_back(bit.query(r-1));
            bit.add(r, 1);
        }
        reverse(ret.begin(), ret.end());
        return ret;
    }
};

 

【493】Reverse Pairs （2019年1月23日，复习Fenwick Tree 和 学习Segment Tree）

给了一个数组，求数组中逆序对的个数。注意这题的逆序对和我们平常定义的有个非常微小的差异。

Given an array nums, we call (i, j) an important reverse pair if i < j and nums[i] > 2*nums[j].

数据规模：

1. The length of the given array will not exceed 50,000.
2. All the numbers in the input array are in the range of 32-bit integer.

Example1:

Input: [1,3,2,3,1]
Output: 2

Example2:

Input: [2,4,3,5,1]
Output: 3

题解：我是用树状数组求的。我们先把数组离散化获得他们的相对大小。然后用排序好了的去重之后的数组下标来作为bit的原始数组，原始数组中所有元素都为0。我们从头开始遍历 nums 数组，对于nums[i]这个元素，首先获取它离散化之后的下标。然后查询从 nums[i] * 2 + 1 到排序数组的最大值的这段区间里面的区间和。累加到ret上面就可以了。注意数据规模 nums[i] 最大可以到 INT_MAX， 最小可以到 INT_MIN，所以 nums[i] * 2 + 1 完全可能超过 int 的范围。

class Solution {
public:
    int reversePairs(vector<int>& nums) {
        const int n = nums.size();
        set<int> st(nums.begin(), nums.end());
        m = st.size();
        summ = vector<int>(m+1, 0);
        map<int, int> mp;
        int idx = 1;
        for (auto e : st) {
            mp[e] = idx++;
        }
        vector<long long> sorted(m+1, 0); //0-based
        int t = 1;
        for (auto e : st) {
            sorted[t++] = e;
        }
        int ret = 0;
        for (int i = 0; i < nums.size(); ++i) {
            int e = nums[i];
            int x = mp[e];
            long long target = 2 * (long long)nums[i];
            int x1 = distance(sorted.begin(), upper_bound(sorted.begin(), sorted.end(), target));
            ret += query(m) - query(x1 - 1);  
            add(x, 1);
        }
        return ret;
    }
    int m;
    vector<int> summ; //bit sum
    void add(int x, int val) {
        for (int i = x; i <= m; i += lowbit(i)) {
            summ[i] += val;
        }
    }
    int query(int x) {
        int res = 0;
        for (int i = x; i > 0; i -= lowbit(i)) {
            res += summ[i];
        }
        return res;
    }
    int lowbit(int x) {
        return x & (-x);
    }
    void print(map<int, int>& mp) {
        for (auto p : mp) {
            cout << p.first << " " << p.second << endl;
        }
    }
    void print(vector<int>& nums) {
        for (auto e : nums) {
            cout << e << " " ;
        }
        cout << endl;
    }
};