【LeetCode】数学(共106题)
【2】Add Two Numbers (2018年12月23日,review)
链表的高精度加法。
题解:链表专题:https://www.cnblogs.com/zhangwanying/p/9797184.html
【7】Reverse Integer (2018年12月23日, review)
给了一个32位的整数,返回它的reverse后的整数。如果reverse后的数超过了整数的范围,就返回 0.
Example 1: Input: 123 Output: 321 Example 2: Input: -123 Output: -321 Example 3: Input: 120 Output: 21
题解:见代码

1 class Solution { 2 public: 3 int reverse(int x) { 4 long long num = x; 5 bool nega = false; 6 if (num < 0) { 7 num = -num; 8 nega = true; 9 } 10 long long ret = 0; 11 while (num) { 12 int mod = num % 10; 13 ret = ret * 10 + mod; 14 num /= 10; 15 } 16 if (nega) {ret = -ret;} 17 if (ret > INT_MAX || ret < INT_MIN) { 18 ret = 0; 19 } 20 return (int) ret; 21 } 22 };
【8】String to Integer (atoi) (2018年12月23日,review)
按照题目给的规则实现 atoi
题解:corner cases 要注意,其他的没啥

1 class Solution { 2 public: 3 int myAtoi(string str) { 4 const int n = str.size(); 5 if (n == 0) {return 0;} 6 if (!isdigit(str[0]) && str[0] != '-' && str[0] != '+' && str[0] != ' ') { 7 return 0; 8 } 9 int firstIdx = 0; 10 while (firstIdx < n && str[firstIdx] == ' ') { 11 ++firstIdx; 12 } 13 if (firstIdx == n || str[firstIdx] != '+' && str[firstIdx] != '-' && !isdigit(str[firstIdx])) { return 0; } 14 string number = string(1, str[firstIdx]); 15 int idx = firstIdx + 1; 16 while (idx < n && isdigit(str[idx])) { 17 number = number + string(1, str[idx]); 18 ++idx; 19 } 20 if (number == "-" || number == "+") {return 0;} 21 int startIdx = isdigit(number[0]) ? 0 : 1; 22 int p = startIdx; 23 while (p < number.size() && number[p] == '0') { 24 ++p; 25 } 26 number = number.substr(0, startIdx) + number.substr(p); 27 28 if (number.size() > 11) { 29 if (number[0] == '-') { 30 return INT_MIN; 31 } 32 return INT_MAX; 33 } 34 long long ret = 0; 35 for (int i = startIdx; i < number.size(); ++i) { 36 ret = ret * 10 + (number[i] - '0'); 37 } 38 if (number[0] == '-') { 39 ret = -ret; 40 } 41 if (ret > INT_MAX) { 42 ret = INT_MAX; 43 } 44 if (ret < INT_MIN) { 45 ret = INT_MIN; 46 } 47 return ret; 48 } 49 };
【9】Palindrome Number (2018年12月23日,review)
判断一个整数是不是回文。(不能转化成string)
题解:如果是负数,直接返回false。正数的话 reverse 一下,看reverse后是否相同。

1 public: 2 bool isPalindrome(int x) { 3 if (x < 0) {return false;} 4 long long num = x; 5 long long reverse = reverseNum(num); 6 return num == reverse; 7 } 8 long long reverseNum(long long num) { 9 long long ret = 0; 10 while (num > 0) { 11 ret = ret * 10 + (num % 10); 12 num /= 10; 13 } 14 return ret; 15 } 16 };
【12】Integer to Roman
【13】Roman to Integer
【29】Divide Two Integers (2019年3月16日,不能用乘除法的两个整数相除)(M)
Given two integers dividend and divisor, divide two integers without using multiplication, division and mod operator.
Return the quotient after dividing dividend by divisor.
The integer division should truncate toward zero.
- Assume we are dealing with an environment which could only store integers within the 32-bit signed integer range: [−2^31, 2^31 − 1]. For the purpose of this problem, assume that your function returns 231 − 1 when the division result overflows.
题解:本题是用divisor不断左移(乘以2)的方式来逼近dividend,然后用dividend来减去这个左移的数字来缩小dividend。重复这个过程直到 dividend 小于 divisor,利用一个变量来记录 divisor 倍增的总次数,用这个来计算答案。
核心代码如下:
//a为被除数,b为除数 int res=0; while (a>=b) { c = b; count=1; while ((c<<1)<=a) { c=c<<1; count=count<<1; } res+=count; a = a-c; }

1 class Solution { 2 public: 3 int divide(int dividend, int divisor) { 4 long long res = 0; 5 bool nega = false; 6 long long a = dividend, b = divisor; 7 if (a < 0) { a = abs(a); nega = !nega; } 8 if (b < 0) { b = abs(b); nega = !nega; } 9 while (a >= b) { 10 long long c = b; 11 long long cnt = 1LL; 12 while ((c << 1) <= a) { 13 c <<= 1; 14 cnt <<= 1; 15 } 16 a -= c; 17 res += cnt; 18 } 19 if (nega) {res = -res;} 20 if (res > INT_MAX || res < INT_MIN) {res = INT_MAX;} 21 return res; 22 } 23 };
【43】Multiply Strings (2018年11月27日,高精度乘法)(2019年1月23日复习,谷歌tag)
给了两个string类型的数字,num1 和 num2, 用string的形式返回 num1 * num2。(num1, num2 的长度都小于等于110)
题解:见 string 分类:https://www.cnblogs.com/zhangwanying/p/9885334.html

1 class Solution { 2 public: 3 string multiply(string num1, string num2) { 4 size1 = num1.size(), size2 = num2.size(); 5 v1 = str2vecAndReverse(num1), v2 = str2vecAndReverse(num2); 6 vector<int> v3(size1 + size2, 0); 7 for (int i = 0; i < size1; ++i) { 8 for (int j = 0 ; j < size2; ++j) { 9 v3[i+j] += v1[i] * v2[j]; 10 v3[i+j+1] += v3[i+j] / 10; 11 v3[i+j] = v3[i+j] % 10; 12 } 13 } 14 string ret = ""; 15 for (auto n : v3) { 16 ret = to_string(n) + ret; 17 } 18 auto p = ret.find_first_not_of('0'); 19 if (p == string::npos) { 20 ret = "0"; 21 } else { 22 ret = ret.substr(p); 23 } 24 return ret; 25 } 26 vector<int> str2vecAndReverse(string num) { 27 int size = num.size(); 28 vector<int> ret(size); 29 for (int i = size - 1; i >= 0; --i) { 30 ret[size-i-1] = num[i] - '0'; 31 } 32 return ret; 33 } 34 int size1 = 0, size2 = 0; 35 vector<int> v1, v2; 36 };
【50】Pow(x, n) (算法群,2018年10月25日)
求double 类型 x 的 n 次幂,注意 x 和 n的大小
- -100.0 < x < 100.0
- n is a 32-bit signed integer, within the range [−2^31, 2^31 − 1 ]
题解:快速幂的基本解法,时间复杂度是 O(logN)。本题需要注意 n 的极小值,当 n = -INT_MIN 的时候,转换成 -n int 类型会溢出,因此 WA 了一次。

1 class Solution { 2 public: 3 double myPow(double x, int n) { 4 double res = 0.0; 5 long long N = (long long)n; // 当 n = —INT_MIN 的时候,int会溢出 6 if (N == 0) {return 1;} 7 if (N < 0) { 8 res = fastPow(x, -N); 9 res = 1.0 / res; 10 } else { 11 res = fastPow(x, N); 12 } 13 return res; 14 } 15 // 快速幂 O(logN) 16 double fastPow(double x, long long n) { 17 if (n == 1) { return x; } 18 double temp = fastPow(x, n / 2); 19 return n & 1 ? temp * temp * x : temp * temp; 20 } 21 };
【60】Permutation Sequence
【65】Valid Number
【66】Plus One
【67】Add Binary
【69】Sqrt(x) (2018年10月26日, 算法群)
返回x的平方根的整数部分。
题解:直接二分法。(这题有人从 1 开始枚举都能过。)stl 的 lower_bound 自己实现了一个, 12ms

1 //lower_bound 的实现 2 class Solution { 3 public: 4 int mySqrt(int x) { 5 int left = 1, right = 1 << 16; 6 int mid = 0; 7 while (left < right) { 8 mid = (left + right) >> 1; 9 if ((long long)mid * mid < (long long)x) { 10 left = mid + 1; 11 } else { 12 right = mid; 13 } 14 } 15 return left * left == x ? left : left -1; 16 } 17 };
顺便提一下 lower_bound 和 upper_bound 的写法。
1 int my_lower_bound(vector<int>& nums, int target) { 2 int left = 0, right = nums.size(); 3 int mid = 0; 4 while (left < right) { 5 mid = (left + right) >> 1; 6 if (nums[mid] < target) { 7 left = mid + 1; 8 } else { 9 right = mid; 10 } 11 } 12 return left; 13 }
1 int my_upper_bound(vector<int>& nums, int target) { 2 int left = 0, right = nums.size(); 3 int mid = 0; 4 while (left < right) { 5 mid = (left + right) >> 1; 6 if (nums[mid] > target) { 7 right = mid; 8 } else { 9 left = mid + 1; 10 } 11 } 12 return left; 13 }
【149】Max Points on a Line (2018年11月10号,算法群)
给了 2D 平面上的 n 个点,两个点能组成一条直线,返回一条直线上最多能有几个点。
Input: [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]] Output: 4 Explanation: ^ | | o | o o | o | o o +-------------------> 0 1 2 3 4 5 6
题解:就是暴力解法,我们先固定一个点,然后用其他点作为另外一个点,确定一条直线的斜率,有 y = kx+b, 有 k 的情况下再加上一个固定的点坐标,这条直线就是确定的。用hash-table来数一条线上最多几个点。
要AC还有两个点需要注意,(1)输入可能有完全重复的点坐标,(2)当有两个点(A, B)足够近但是他们两个距离第三个点(C)足够远的时候,这个时候AC 和 BC 的斜率可能会爆double,就是 A B C并不在同一条直线上,但是AC 和BC算出来的斜率一样。这种可用求gcd约分处理。

1 /** 2 * Definition for a point. 3 * struct Point { 4 * int x; 5 * int y; 6 * Point() : x(0), y(0) {} 7 * Point(int a, int b) : x(a), y(b) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 int maxPoints(vector<Point>& points) { 13 const int n = points.size(); 14 if (n < 3) {return n;} 15 map<pair<int, int>, int> slope_cnt; //在固定一个点的情况下,选择周围所有的点,计算斜率。 16 int ret = 0; 17 for (int i = 0; i < n - 1; ++i) { //固定一个点 18 int numOfi = 0; 19 slope_cnt.clear(); 20 Point p1 = points[i]; 21 int samePoint = 0; //与 p1 重合点的个数 22 for (int j = i + 1; j < n; ++j) { //选另外一个点 23 Point p2 = points[j]; 24 pair<int, int> slope; 25 if (p1.x == p2.x) { //没有斜率,两个点与y轴平行; 或者两个点重合 26 if (p1.y == p2.y) { samePoint++; continue;} 27 slope = make_pair(std::numeric_limits<int>::infinity(), std::numeric_limits<int>::infinity()); 28 } else { 29 int dy = p1.y - p2.y, dx = p1.x - p2.x; 30 int gcd = __gcd(dy, dx); 31 slope = make_pair(dy/gcd, dx/gcd); 32 } 33 if (slope_cnt.find(slope) != slope_cnt.end()) { 34 slope_cnt[slope]++; 35 } else { 36 slope_cnt[slope] = 2; 37 } 38 } 39 numOfi = samePoint + 1; 40 for (auto p : slope_cnt) { 41 numOfi = max(numOfi, p.second + samePoint); 42 } 43 ret = max(ret, numOfi); 44 } 45 return ret; 46 } 47 };
【166】Fraction to Recurring Decimal
【168】Excel Sheet Column Title (2018年12月23日,review)
给了一个数字 n,返回 n 代表的 excel title。
For example:
1 -> A
2 -> B
3 -> C
...
26 -> Z
27 -> AA
28 -> AB
...
Example 1:
Input: 1
Output: "A"
Example 2:
Input: 28
Output: "AB"
Example 3:
Input: 701
Output: "ZY"
题解:26进制

1 class Solution { 2 public: 3 string convertToTitle(int n) { 4 string ret = ""; 5 while (n > 0) { 6 n--; 7 int mod = n % 26; 8 char c = 'A' + mod; 9 ret = string(1, c) + ret; 10 n /= 26; 11 } 12 return ret; 13 } 14 };
【171】Excel Sheet Column Number (2018年12月23日,review)
与168题相反,本题是给了一个 string s 代表 excel 的title,问这个 s 是第几列。
题解:26进制

1 class Solution { 2 public: 3 int titleToNumber(string s) { 4 int ret = 0; 5 const int n = s.size(); 6 int pow = 1; 7 for (int i = n-1; i >= 0; --i) { 8 ret += pow * (s[i] - 'A' + 1); 9 pow *= 26; 10 } 11 return ret; 12 } 13 };
【172】Factorial Trailing Zeroes (2018年12月23日,周日,算法群)
给了一个数字 n,返回 n! 的结尾 0 有几个。
题解:结尾 0 的个数只和因子里面的 5 的个数有关系。比如 5! 后面有 1 个结尾 0, 10!后面有两个结尾 0。(其实和 2 的个数也有关系,但是 2 的个数肯定比 5 的个数多。)

1 class Solution { 2 public: 3 int trailingZeroes(int n) { 4 int ret = 0; 5 while (n > 0) { 6 ret += n / 5; 7 n /= 5; 8 } 9 return ret; 10 } 11 };
【202】Happy Number
【204】Count Primes
【223】Rectangle Area
【224】Basic Calculator (2018年11月16日,算法群)
给了一个字符串算式,里面有数字,有“+”, “-” , “ ” , 和 “(” , ")"。问算式最后结果是多少,返回int。
题解:本题的题解写在了 stack 专题里面:https://www.cnblogs.com/zhangwanying/p/9886577.html
【231】Power of Two (2018年11月16日,随手复习了一下)
给了一个整数 n, 返回 n 是不是2的幂。
题解:复习一把。注意 n 如果是负数直接返回false。还有括号能多加就多加,不然可能发生你意想不到的情况orz

1 class Solution { 2 public: 3 bool isPowerOfTwo(int n) { 4 return n > 0 && (n & (n-1)) == 0; 5 } 6 };
【233】Number of Digit One (2019年4月12日,数数题)
给定一个正整数 N, 返回一个整数,代表 0 ~ N 之间所有数字中 1 的个数。
Example: Input: 13 Output: 6 Explanation: Digit 1 occurred in the following numbers: 1, 10, 11, 12, 13.
题解:我们可以举个例子来发现规律。
举个例子54215,比如现在求百位上的1,54215的百位上是2。可以看到xx100到xx199的百位上都是1,这里xx从0到54,即100->199, 1100->1199…54100->54199, 这些数的百位都是1,因此百位上的1总数是55*100。
如果n是54125,这时由于它的百位是1,先看xx100到xx199,其中xx是0到53,即54*100, 然后看54100到54125,这是26个。所以百位上的1的总数是54*100 + 26.
如果n是54025,那么只需要看xx100到xx199中百位上的1,这里xx从0到53,总数为54*100
求其他位的1的个数的方法是一样的。
所以,规律如下:
要求第i位1出现的次数,并且i的高位数为highN,低位数为lowN,当前第i位的数字为cdigit,则当前i位1出现的次数分三种情况:

代码也并不好写。

1 class Solution { 2 public: 3 int countDigitOne(int n) { 4 int res = 0; 5 int high = n, low = 0; 6 long long fac = 1LL; 7 while (n / fac) { 8 int num = (n % (fac * 10)) / fac; 9 high /= 10; 10 if (num == 0) { 11 res += high * fac; 12 } 13 if (num == 1) { 14 res += (high) * fac + (low + 1); 15 } 16 if (num >= 2) { 17 res += (high + 1) * fac; 18 } 19 low = num * fac + low; 20 fac *= 10; 21 } 22 return res; 23 } 24 };
【246】Strobogrammatic Number
【247】Strobogrammatic Number II
【248】Strobogrammatic Number III
【258】Add Digits
【263】Ugly Number
【264】Ugly Number II
【268】Missing Number
【273】Integer to English Words (2019年2月12日)
把一个int类型的数字给读出来。
Input: 1234567891 Output: "One Billion Two Hundred Thirty Four Million Five Hundred Sixty Seven Thousand Eight Hundred Ninety One"
题解:从右边到左边,三个一段。(代码写的一般==)

1 class Solution { 2 public: 3 vector<string> list = {"", " Thousand", " Million", " Billion"}; 4 string numberToWords(int num) { 5 initMp(); 6 int level = 0; 7 string res = ""; 8 if (num == 0) {return mp[0];} 9 while (num) { 10 int temp = num % 1000; 11 string tempAns = trans(temp); 12 if (!tempAns.empty()) { 13 tempAns += list[level]; 14 res = tempAns + (res.empty() ? res : " " + res); 15 } 16 num /= 1000; 17 ++level; 18 } 19 return res; 20 } 21 unordered_map<int, string> mp; 22 string trans(int num) { 23 string str = to_string(num); 24 if (str.size() < 3) { str = string((3 - str.size()), '0') + str; } 25 string res = ""; 26 if (str[0] != '0') { res = mp[str[0]-'0'] + " Hundred"; } 27 if (str[1] != '0') { 28 int temp = 0; 29 if (str[1] == '1') { 30 temp = (str[1]-'0') * 10 + (str[2]-'0'); 31 } else { 32 temp = (str[1]-'0') * 10; 33 } 34 res += res.empty() ? mp[temp] : " " + mp[temp]; 35 } 36 if (str[2] != '0' && str[1] != '1') { 37 res += res.empty() ? mp[(str[2] - '0')] : " " + mp[(str[2] - '0')]; 38 } 39 return res; 40 } 41 void initMp() { 42 mp[0] = "Zero", mp[1] = "One", mp[2] = "Two", mp[3] = "Three", mp[4] = "Four", mp[5] = "Five", mp[6] = "Six", 43 mp[7] = "Seven", mp[8] = "Eight", mp[9] = "Nine", mp[10] = "Ten", mp[11] = "Eleven", mp[12] = "Twelve", 44 mp[13] = "Thirteen", mp[14] = "Fourteen", mp[15] = "Fifteen", mp[16] = "Sixteen", mp[17] = "Seventeen", 45 mp[18] = "Eighteen", mp[19] = "Nineteen", mp[20] = "Twenty", mp[30] = "Thirty", mp[40] = "Forty", 46 mp[50] = "Fifty", mp[60] = "Sixty", mp[70] = "Seventy", mp[80] = "Eighty", mp[90] = "Ninety"; 47 } 48 };
【279】Perfect Squares
这题 dp/bfs 出现过。
【296】Best Meeting Point (2018年11月22日,开始冲hard)
给了一个二维的 0/1 矩阵grid, grid[i][j] = 1 代表 1 位置上有个人,现在矩阵上至少有两个人,这几个人想挑一个点 (x, y) 相会,问矩阵上的哪个点到这几个人的曼哈顿距离和最近,返回最近的距离之和。
题解可以见 sort分类里面的题解:https://www.cnblogs.com/zhangwanying/p/9914941.html
【313】Super Ugly Number
【319】Bulb Switcher
【326】Power of Three
【335】Self Crossing
【343】Integer Break
【356】Line Reflection
【357】Count Numbers with Unique Digits
【360】Sort Transformed Array
【365】Water and Jug Problem
【367】Valid Perfect Square (算法群,2018年10月27日)
给了一个正整数 num,判断是不是完全平方数。不能直接开根号。
题解:(1)我的解法非常挫,把 root 从 1 开始遍历,如果 root * root == num 就是,否则 root++。 如果 root * root > num,就直接退出。

1 // O(N) 2 class Solution { 3 public: 4 bool isPerfectSquare(int num) { 5 int root = 1; 6 while (root <= num/2+1) { 7 if (root * root == num) { return true; } 8 else if ((long long)root * root > num) { return false; } 9 root++; 10 } 11 return false; 12 } 13 };
(2)本题也可以用二分解。 (直接lower_bound)

1 //binary search 妈呀,WA了好几次。 2 class Solution { 3 public: 4 bool isPerfectSquare(int num) { 5 int left = 1, right = num / 2 + 2; 6 int mid = 0; 7 while (left < right) { 8 mid = (left + right) / 2; 9 long long temp = (long long) mid * mid; 10 if (temp < num) { 11 left = mid + 1; 12 } else { 13 right = mid; 14 } 15 } 16 return left * left == num; 17 } 18 };
(3)数学方法,一个完全平方数等于从 1 开始的连续奇数和。
证明就是这张图: 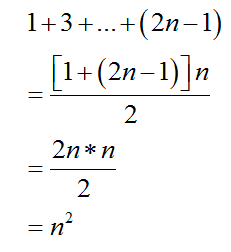

1 //奇数和 2 class Solution { 3 public: 4 bool isPerfectSquare(int num) { 5 int i = 1; 6 while (num > 0) { 7 num -= i; 8 i += 2; 9 } 10 return num == 0; 11 } 12 };
【368】Largest Divisible Subset
【372】Super Pow
【396】Rotate Function
【397】Integer Replacement (2019年2月3日,算法群打卡题)
给了一个 int n,如果 n 是奇数的话,就可以把 n 加一或者减一,如果 n 是偶数的话,就可以把 n 除以 2. 返回把 n 变成 1 的最小步数。
题解:我自己是用 bfs 解的。本题也能用 dfs 或者 数学解法。下面说下数学解法。如果说当前数字 n 的二进制结尾是 11,那么就把它加一,凑成 4 的倍数。(但是 3 是个例外)。如果是其他的奇数的话,就全部 减一。

1 class Solution { 2 public: 3 int integerReplacement(int m) { 4 int cnt = 0; 5 long long n = m; 6 while (n > 1) { 7 if (n & 1) { 8 if ((n & 2) && (n != 3)) { 9 n += 1; 10 } else { 11 n -= 1; 12 } 13 } else { 14 n >>= 1; 15 } 16 ++cnt; 17 } 18 return cnt; 19 } 20 };
【400】Nth Digit (2019年3月14日,算法群打卡题)(M)
Find the nth digit of the infinite integer sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...
Note:n is positive and will fit within the range of a 32-bit signed integer (n < 2^31).
Example 1: Input: 3 Output: 3 Example 2: Input: 11 Output: 0 Explanation: The 11th digit of the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... is a 0, which is part of the number 10.
题解:这个题我们可以分成三步,第一步是找到这个数字落在第几位数身上,第二步是把这个 k 位数找出来,第三步是找到这个 k 位数对应的digit。

1 class Solution { 2 public: 3 int findNthDigit(int n) { 4 //step 1. find len digits number 5 int len = 1; 6 int start = 1; 7 long count = 9; 8 while (n > len * count) { 9 n -= len * count; 10 len++; 11 start *= 10; 12 count *= 10; 13 } 14 //step 2. get number 15 int number = start + (n-1) / len; 16 //step 3. return exactly digit 17 string strNum = to_string(number); 18 return strNum[(n-1)%len] - '0'; 19 } 20 };
【413】Arithmetic Slices
【415】Add Strings
【423】Reconstruct Original Digits from English
【441】Arranging Coins
【453】Minimum Moves to Equal Array Elements
【462】Minimum Moves to Equal Array Elements II
【469】Convex Polygon
【478】Generate Random Point in a Circle
【483】Smallest Good Base
【507】Perfect Number (2018年11月25日)
We define the Perfect Number is a positive integer that is equal to the sum of all its positive divisors except itself.
Now, given an integer n, write a function that returns true when it is a perfect number and false when it is not.
Example: Input: 28 Output: True Explanation: 28 = 1 + 2 + 4 + 7 + 14
Note: The input number n will not exceed 100,000,000. (1e8)
题解:我第一次Ac的时候是用了遍历到 num/2 这个范围,但是其实遍历到 sqrt(num) 这个范围就行了。(本来 beats 10%, 现在beats 100%)

1 class Solution { 2 public: 3 bool checkPerfectNumber(int num) { 4 if (num == 0) {return false;} 5 int summ = 0; 6 for (int k = 1; k * k <= num; ++k) { 7 if (num % k == 0) { 8 summ += k; 9 summ += k == num / k ? 0 : num / k; 10 } 11 } 12 return summ == 2 * num; 13 } 14 };
【517】Super Washing Machines
【523】Continuous Subarray Sum
【535】Encode and Decode TinyURL
【537】Complex Number Multiplication (2018年11月27日)
给了两个字符串,代表两个 complex, 返回这两个complex 的乘积(用字符串表示)。
题解:先分解这两个字符串分解出实数和虚数部分,然后分别求乘积的实数部分和虚数部分。

1 class Solution { 2 public: 3 string complexNumberMultiply(string a, string b) { 4 vector<int> num1 = split(a), num2 = split(b); 5 if (num1.empty() || num2.empty()) {return "err";} 6 vector<int> num(2); 7 num[0] = num1[0] * num2[0] - num1[1] * num2[1]; 8 num[1] = num1[0] * num2[1] + num1[1] * num2[0]; 9 string ret = to_string(num[0]) + "+" + to_string(num[1]) + "i"; 10 return ret; 11 } 12 vector<int> split(string s) { 13 vector<int> ans(2); 14 auto pos = s.find("+"); 15 if (pos == string::npos) { 16 return vector<int>(); 17 } 18 string s1 = s.substr(0, pos); 19 string s2 = s.substr(pos+1, s.size()-pos-1); 20 //printf("s1 = %s, s2 = %s \n", s1.c_str(), s2.c_str()); 21 ans[0] = stoi(s1), ans[1] = stoi(s2); 22 return ans; 23 } 24 };
【553】Optimal Division (2019年3月27日,算法群打卡题)
给定一个数组,相邻的数字会进行除法计算。 For example, [2,3,4] -> 2 / 3 / 4. 可以加括号,改变除法的优先级,问这个算式的最大值。返回的不是值,而是表达式。
Input: [1000,100,10,2] Output: "1000/(100/10/2)" Explanation: 1000/(100/10/2) = 1000/((100/10)/2) = 200 However, the bold parenthesis in "1000/((100/10)/2)" are redundant, since they don't influence the operation priority. So you should return "1000/(100/10/2)". Other cases: 1000/(100/10)/2 = 50 1000/(100/(10/2)) = 50 1000/100/10/2 = 0.5 1000/100/(10/2) = 2
Note:
- The length of the input array is [1, 10].
- Elements in the given array will be in range [2, 1000].
- There is only one optimal division for each test case.
题解:这题乍看是dfs,但是其实通过观察,我们可以发现一个非常巧妙的方法来计算这个题。我们想让除法的商最大,那么显然我们想要扩大分子,缩小分母。显然第一个数肯定是要做分子的,那么我们能做的就是缩小分母。因为给定的都是正整数,所以把除了第一个数字之外的所有数字都用括号括起来,做分母,这样分母就能最大。

1 class Solution { 2 public: 3 string optimalDivision(vector<int>& nums) { 4 string res = ""; 5 if (nums.size() == 1) {return res = to_string(nums.front());} 6 if (nums.size() == 2) {return res = to_string(nums.front()) + "/" + to_string(nums.back());} 7 res = to_string(nums.front()) + "/(" ; 8 for (int i = 1; i < nums.size(); ++i) { 9 res += to_string(nums[i]) + "/"; 10 } 11 res.pop_back(); 12 res += ")"; 13 return res; 14 } 15 };
【573】Squirrel Simulation
【592】Fraction Addition and Subtraction
【593】Valid Square (2019年3月28日)
给了四个点,判断这四个点能不能形成正方形。
题解:我看了discuss的解法,里面说,两两计算两点之间的距离,然后把距离都加进一个hashset里面,最后hashset里面只剩两个元素,然后没有 0 元素,这样就能构成一个正方形。

1 class Solution { 2 public: 3 bool validSquare(vector<int>& p1, vector<int>& p2, vector<int>& p3, vector<int>& p4) { 4 unordered_set<int> st; 5 st.insert(dis(p1, p2)); 6 st.insert(dis(p1, p3)); 7 st.insert(dis(p1, p4)); 8 st.insert(dis(p2, p3)); 9 st.insert(dis(p2, p4)); 10 st.insert(dis(p3, p4)); 11 return st.size() == 2 && !st.count(0); 12 } 13 int dis(vector<int>& p1, vector<int>& p2) { 14 return (p1[0] - p2[0]) * (p1[0] - p2[0]) + (p1[1] - p2[1]) * (p1[1] - p2[1]); 15 } 16 };
【598】Range Addition II
【625】Minimum Factorization
【628】Maximum Product of Three Numbers
【633】Sum of Square Numbers (算法群,2018年10月29日)
给了一个非负整数 c,判断他是否能表达成 两个整数的平方和。
Input: 5 Output: True Explanation: 1 * 1 + 2 * 2 = 5
题解:我一开始想的是 2 pointers 直接搞一下,结果是直接AC了,后来看了下群里大家的答案,都是二分,所以我也写个二分好了。2 pointers 的时间复杂度是 O(sqrt(c)), 二分的时间复杂度是 O(sqrt(c) * log(c))

1 class Solution { 2 public: 3 bool judgeSquareSum(int c) { 4 int p1 = 0, p2 = sqrt(c) + 1; 5 int summ = p1 * p1 + p2 * p2; 6 while (p1 <= p2) { 7 if (summ == c) { 8 return true; 9 } else if (summ > c) { 10 p2--; 11 } else if (summ < c) { 12 p1++; 13 } 14 summ = p1 * p1 + p2 * p2; 15 } 16 return false; 17 } 18 };

1 class Solution { 2 public: 3 bool judgeSquareSum(int c) { 4 for (int p1 = 0; p1 < sqrt(c) + 1; ++p1) { 5 int target = c - p1 * p1; 6 int left = 0, right = sqrt(target) + 1; 7 int t = my_lower_bound(left, right + 1, target); 8 if (t * t == target) { 9 return true; 10 } 11 } 12 return false; 13 } 14 int my_lower_bound(int left, int right, int target) { 15 while (left < right) { 16 int mid = (left + right) / 2; 17 if (mid * mid < target) { 18 left = mid + 1; 19 } else { 20 right = mid; 21 } 22 } 23 return left; 24 } 25 };
本题还有一种解法是用了「费马平方和定理」,有空可以研究一下。https://leetcode.com/problems/sum-of-square-numbers/solution/ (solution #5)
【634】Find the Derangement of An Array
【640】Solve the Equation
【645】Set Mismatch
【651】4 Keys Keyboard
【660】Remove 9
【670】Maximum Swap
【672】Bulb Switcher II
【728】Self Dividing Numbers
【753】Cracking the Safe
【754】Reach a Number
【775】Global and Local Inversions
【780】Reaching Points
【781】Rabbits in Forest (2019年2月14日,Medium)
在一个森林中,每只兔子都有一个颜色,给了一个数组代表兔子的子集,数组的一个元素 nums[i] = x 代表除了它本身,森林里面还有多少只兔子跟他一样颜色。返回一个数值,代表森林里面最少多少只兔子。
题解:if a rabbit answer x, then it will have x+1 rabbits in its group. now n rabbits answers x.
if n % (x+1) == 0, we need n / (x+1) groups of x + 1 rabbits.
if n % (x+1) != 0, we need n / (x+1) + 1 groups of x + 1 rabbits.

1 class Solution { 2 public: 3 int numRabbits(vector<int>& answers) { 4 const int n = answers.size(); 5 unordered_map<int, int> mp; 6 //统计每个兔子报数的频次。 7 for (auto num : answers) { mp[num]++; } 8 // if x rabbits answer x, then we have x + 1 rabbits have the same color. 9 int res = 0; 10 for (auto& p : mp) { 11 int key = p.first, value = p.second; 12 int k = value / (key + 1); 13 res += k * (key + 1); 14 int left = value % (key + 1); 15 res += left > 0 ? (key + 1) : 0; 16 } 17 return res; 18 } 19 };
【782】Transform to Chessboard
【789】Escape The Ghosts
【794】Valid Tic-Tac-Toe State (Oct 15th, 2018 每日一题)
通过字符串数组给定一个Tic-Tac-Toe(三连棋游戏,两人轮流在九格方盘上画'X'或者'O',谁先把三个相同记号排成横线、直线、斜线,即是胜者)状态board。 返回True如果当且仅当这个状态是一个有效的状态。 board是3x3数组,包含字符" ", "X", "O"。" "字符代表空的格。
Tic-Tac-Toe游戏规则:
- 玩家只能轮流在空格(" ")里面画字符。
- 第一个玩家总是画"X",第二个玩家总是画"O"。
- "X"和"O"只能画在空白的格里面,不能画在已经存在"O"和"X"的格里。
- 三个相同记号排成横线、直线、斜线,即游戏结束。
- 如果没有空的格,游戏也结束。
- 游戏结束不能再移动。
Example 1: Input: board = ["O ", " ", " "] Output: false Explanation: The first player always plays "X". Example 2: Input: board = ["XOX", " X ", " "] Output: false Explanation: Players take turns making moves. Example 3: Input: board = ["XXX", " ", "OOO"] Output: false Example 4: Input: board = ["XOX", "O O", "XOX"] Output: true
题解:参考知乎:https://zhuanlan.zhihu.com/p/34216982
首先我们要先熟悉下Tic-Tac-Toe三连棋游戏规则,就是两人轮流在九格方盘上画'X'或者'O',谁先把三个相同记号排成横线、直线、斜线,即游戏结束。
那么我们从游戏规则中来找处所有不合理的状态。
根据规则1和2,假设X的数目为countX, O的数目为countO,那么我们可以得到countX==countO,或者countX - countO == 1。
根据游戏结束后则不能再画O和X,那么当countX==count时,如果存在三个X排成横线、直线、斜线,那么即是不合理的,因为X先画,当三个X排成横线、直线、斜线时, 此时游戏结束,不能再画O,所以O的数目应该比X的数目少1。
当countX - countO == 1时,如果存在三个O排成横线、直线、斜线,那么是不合理的,因为当三个O排成横线、直线、斜线时,游戏结束,不能再画X,所以此时X的数目应该和O的数目相等。

1 class Solution { 2 public: 3 bool validTicTacToe(vector<string>& board) { 4 int cntX = 0, cntO = 0; 5 6 //1. X的个数要么和O个数相同,要么X个数比O的个数多一个 7 for (int i = 0; i < 3; ++i) { 8 for (int j = 0; j < 3; ++j) { 9 board[i][j] == 'X' ? cntX++ : board[i][j] == 'O' ? cntO++ : 1; 10 } 11 } 12 if (cntX != cntO && cntX != cntO+1) { 13 return false; 14 } 15 16 //2. 判断最后一个放棋的是X,还是O 17 if (cntX - cntO == 1) { 18 //X最后放的棋子,所以每行,每列,每个对角线O不能有三连。 19 if(check(board, 'O') == false) { 20 return false; 21 } 22 } else if (cntX == cntO) { 23 //O最后放的棋子,所以每行,每列,每个对角线X不能有三连。 24 if(check(board, 'X') == false) { 25 return false; 26 } 27 } 28 return true; 29 } 30 bool check(vector<string>& board, char c) { 31 for (int i = 0; i < 3; ++i) { 32 string target = string(3, c); 33 if (board[i] == target) { return false;} // rows 34 if (board[0][i] == board[1][i] && board[1][i] == board[2][i] && board[0][i] == c) { return false; } // cols 35 } 36 if (board[0][0] == board[1][1] && board[0][0] == board[2][2] && board[0][0] == c) { return false; } 37 if (board[0][2] == board[1][1] && board[1][1] == board[2][0] && board[0][2] == c) { return false; } 38 return true; 39 } 40 };
【800】Similar RGB Color
【805】Split Array With Same Average
【810】Chalkboard XOR Game
【812】Largest Triangle Area (2019年4月12日)
给了若干个平面上的点,问他们能组成三角形的最大面积。
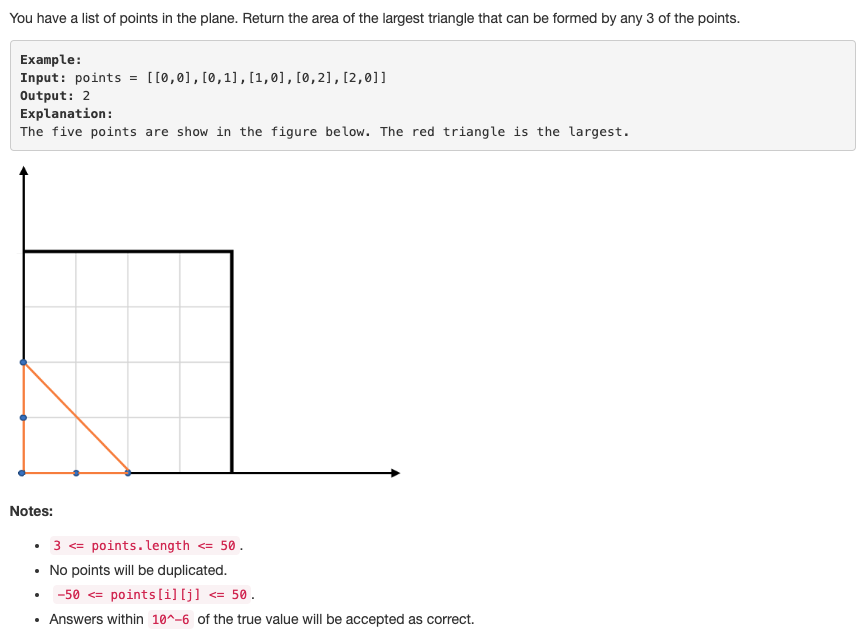
题解:我们可以根据向量的叉积来计算三角形的面积。(初高中数学都快还给老师了。)这个向量相关的一定要会。
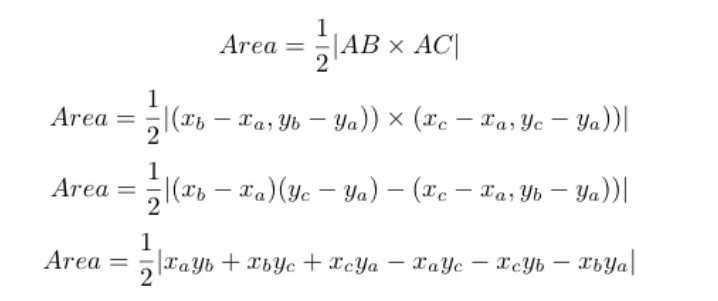
代码如下:

1 class Solution { 2 public: 3 double largestTriangleArea(vector<vector<int>>& points) { 4 double res = 0.0; 5 for (auto& p1 : points) { 6 for (auto& p2 : points) { 7 for (auto& p3 : points) { 8 double temp = 0.5 * ((p1[0] - p2[0]) * (p1[1] - p3[1]) - (p1[1] - p2[1]) * (p1[0] - p3[0])); 9 res = max(temp, res); 10 } 11 } 12 } 13 return res; 14 } 15 };
【829】Consecutive Numbers Sum
【836】Rectangle Overlap (2019年3月12日)
判断两个矩形是否有重叠部分。重叠部分是说重叠的面积大于0,如果是顶点重合或者边重合,则不算重叠。如果这两个矩形重合就返回 true,否则返回 false。
我们用矩形的 左上角 和 右下角 坐标表示一个矩形。
题解:我们想一想如何判断两条 1D 的线段重叠。一定存在一个 x,
left1 < x < right1 && left2 < x < right2
======> left1 < x < right2 && left2 < x < right1
======> left1 < righ2 && left2 < right1
同理,变成2D之后,矩形的 x 方向和 y 方向分别是 独立的 1D。所以代码如下:
1 //如果是1D,判断两个线段是否相交,就是 l1 < r2 && l2 < l1 2 class Solution { 3 public: 4 bool isRectangleOverlap(vector<int>& rec1, vector<int>& rec2) { 5 return rec1[0] < rec2[2] && rec2[0] < rec1[2] && rec1[1] < rec2[3] && rec2[1] < rec1[3]; 6 } 7 };
【858】Mirror Reflection
【866】Prime Palindrome (2018年11月3日, 和 906 超级回文数一起复习了一下)
找出大于等于 N 的第一个回文素数。
题解:先介绍一下我的方法,怎么求 比 N 大的第一个回文数,然后判断它是不是素数,不是素数,就获取下一个回文数。

1 //先构造回文,再判断是不是素数,比 N 大的回文数怎么构造。 2 class Solution { 3 public: 4 int primePalindrome(int N) { 5 if (isPalindrome(N) && isPrime(N)) { 6 return N; 7 } 8 int palin = N; 9 do { 10 //printf("palin = %d \n", palin); 11 palin = getNextGreaterPalindrome(palin); 12 13 } while (!isPrime(palin)); 14 return palin; 15 } 16 bool isPalindrome(int num) { 17 string strN = to_string(num); 18 int start = 0, end = strN.size()-1; 19 while (start < end) { 20 if (strN[start] != strN[end]) { 21 return false; 22 } 23 start++, end--; 24 } 25 return true; 26 } 27 bool isPrime(int num) { 28 if (num == 1) {return false;} 29 for (int i = 2; i <= sqrt(num); ++i) { 30 if (num % i == 0) { 31 return false; 32 } 33 } 34 return true; 35 } 36 int getNextGreaterPalindrome(int num) { 37 if (num <= 9) { 38 return num == 9 ? 11 : num + 1; 39 } 40 string strNum = to_string(num); 41 const int n = strNum.size(); 42 int halfIdx = (n - 1) / 2; //n = 3, halfIdx = 1; n = 4, halfIdx = 1; 43 string strHalf = "", strNew = ""; 44 if (n & 1) { //odd size 45 int p1 = halfIdx - 1, p2 = halfIdx + 1; 46 while (p1 >= 0 && p2 < n) { 47 if (strNum[p1] != strNum[p2]) { 48 break; 49 } 50 p1--, p2++; 51 } 52 if (p1 == -1 || strNum[p1] < strNum[p2]) { //increase by 1 53 strHalf = strNum.substr(0, halfIdx + 1); 54 int intHalf = atoi(strHalf.c_str()); 55 ++intHalf; 56 string strHalfNew = to_string(intHalf); 57 string t = strHalfNew.substr(0, strHalfNew.size()-1); 58 reverse(t.begin(), t.end()); 59 strNew = strHalfNew + t; 60 61 } else { 62 strHalf = strNum.substr(0, halfIdx); 63 string t = strHalf; 64 reverse(t.begin(), t.end()); 65 strNew = strHalf + strNum[halfIdx] + t; 66 } 67 } else { // even size 68 int p1 = halfIdx, p2 = halfIdx + 1; 69 while (p1 >= 0 && p2 < n) { 70 if (strNum[p1] != strNum[p2]) { 71 break; 72 } 73 p1--, p2++; 74 } 75 //printf("p1 = %d, p2 = %d ,strNum[p1] = %c, strNum[p2] = %c \n", p1, p2, strNum[p1], strNum[p2]); 76 if (p1 == -1 || strNum[p1] < strNum[p2]) { //increase by 1 77 strHalf = strNum.substr(0, halfIdx + 1); 78 int intHalf = atoi(strHalf.c_str()); 79 ++intHalf; 80 string strHalfNew = to_string(intHalf); 81 string t = strHalfNew; 82 reverse(t.begin(), t.end()); 83 84 // 是否有进位。。。 85 if ((int)strHalfNew.size() != (int)strHalf.size()) { 86 strNew = strHalfNew + t.substr(1, (int)strHalfNew.size()-1); 87 } else { 88 strNew = strHalfNew + t; 89 } 90 } else { 91 strHalf = strNum.substr(0, halfIdx + 1); 92 string t = strHalf; 93 reverse(t.begin(), t.end()); 94 strNew = strHalf + t; 95 } 96 } 97 98 //string -> int 99 int res = atoi(strNew.c_str()); 100 return res; 101 } 102 103 104 };
genNextPalindrome 这个函数应该可以写的更短一些。等到更新之后放上来。
2019年3月12日更新,如何生成比num大的下一个回文数字。这次写的更短了一些。

1 class Solution { 2 public: 3 int primePalindrome(int N) { 4 if (!isPalindrome(N)) { 5 N = genNextPalindrome(N); 6 } 7 do { 8 if (isPrime(N)) { break; } 9 } while (N = genNextPalindrome(N)); 10 return N; 11 } 12 bool isPrime(int num) { 13 if (num <= 1) {return false;} 14 for (int k = 2; k <= sqrt(num); ++k) { 15 if (num % k == 0) {return false;} 16 } 17 return true; 18 } 19 bool isPalindrome(int N) { 20 string str = to_string(N); 21 int start = 0, end = str.size() -1 ; 22 while (start < end) { 23 if (str[start++] != str[end--]) {return false;} 24 } 25 return true; 26 } 27 int genNextPalindrome(int num) { 28 string str = to_string(num); 29 int size = str.size(); 30 string strHalf = str.substr(0, (size + 1)/2); 31 int iHalf = stoi(strHalf); 32 set<int> candidate; 33 for (int k = 0; k <= 1; ++k) { 34 string temp = to_string(iHalf + k); 35 temp += size & 1? string(temp.rbegin()+1, temp.rend()) : string(temp.rbegin(), temp.rend()); 36 candidate.insert(stoi(temp)); 37 } 38 int size2 = strHalf.size(); 39 int base = pow(10, size) + 1; 40 candidate.insert(base); 41 int diff = INT_MAX; 42 int res = -1; 43 for (auto& c : candidate) { 44 if (c > num && c - num < diff) { 45 diff = c - num; 46 res = c; 47 } 48 } 49 return res; 50 } 51 };
【868】Binary Gap
【869】Reordered Power of 2
【877】Stone Game
【878】Nth Magical Number
【883】Projection Area of 3D Shapes
【885】Spiral Matrix III (2019年4月19日,打卡题)
旋转矩阵,返回填写的坐标。给了一个start的坐标,要求按照顺时针方向填满矩阵。
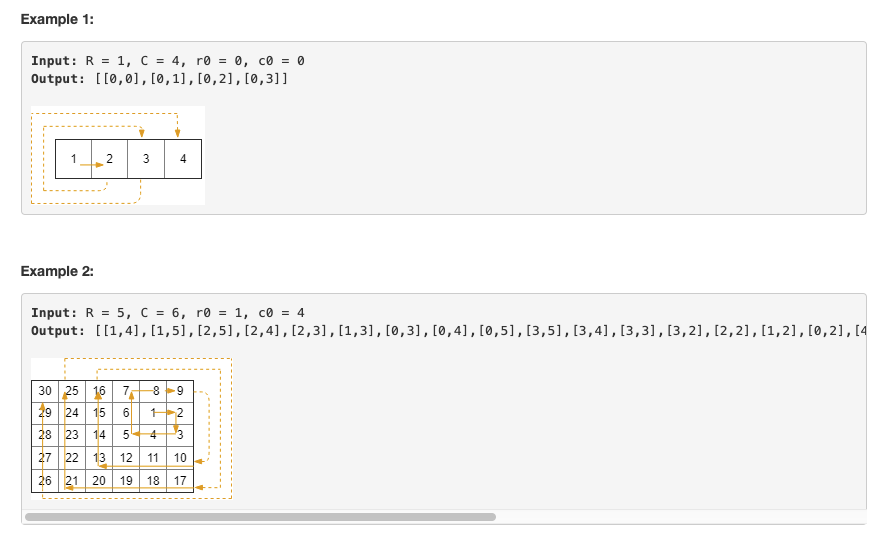
题解:模拟。计算每次走的步数,用个变量 step 表示。时间复杂度是O(RC)

1 class Solution { 2 public: 3 vector<vector<int>> spiralMatrixIII(int R, int C, int r0, int c0) { 4 vector<vector<int>> res; 5 int cnt = 0, tot = R * C, step = 1; 6 int x = r0, y = c0; 7 while (cnt < tot) { 8 for (int i = 0; i < step; ++i) { 9 if (x >= 0 && x < R && y >= 0 && y < C && cnt < tot) { res.push_back({x, y}); ++cnt;} 10 ++y; 11 } 12 for (int i = 0; i < step; ++i) { 13 if (x >= 0 && x < R && y >= 0 && y < C && cnt < tot) { res.push_back({x, y}); ++cnt;} 14 ++x; 15 } 16 ++step; 17 for (int i = 0; i < step; ++i) { 18 if (x >= 0 && x < R && y >= 0 && y < C && cnt < tot) { res.push_back({x, y}); ++cnt;} 19 --y; 20 } 21 for (int i = 0; i < step; ++i) { 22 if (x >= 0 && x < R && y >= 0 && y < C && cnt < tot) { res.push_back({x, y}); ++cnt;} 23 --x; 24 } 25 ++step; 26 } 27 return res; 28 } 29 };
【887】Super Egg Drop
【891】Sum of Subsequence Widths
【892】Surface Area of 3D Shapes
【899】Orderly Queue



 浙公网安备 33010602011771号
浙公网安备 33010602011771号