【CF1044B Intersecting Subtrees】题解

题目链接

题目

这是一道交互题

你和$Li\ Chen$正在玩一个奇怪的游戏。给出一棵$N$个点的树，双方分别给顶点编号为$1$到$N$，双方都不知道对方给树编号的方式。

接着双方在自己对应的树上选择一个联通子图，在你的编号方式对应的树上你选择了$x_1,x_2,...,x_{k_1}$，在$Li\ Chen$的编号方式对应的树上$Li\ Chen$选择了$y_1,y_2,...,y_{k_2}$，双方都知道$x_1,...,x_{k_1}$与$y_1,...,y_{k_2}$的值

现在你想知道两个子图是否存在至少一个公共点。你可以进行询问，问题有以下两种：

$A \ x$：得到在你的编号方式下的$x$号点在$Li\ Chen$的编号方式下的值

$B \ x$：得到在$Li\ Chen$的编号方式下的$x$号点在你的编号方式下的值

现在请你使用不多于$5$次询问得出是否存在公共点，或者确定两棵子树没有公共点。

You are playing a strange game with Li Chen. You have a tree with $n$ nodes drawn on a piece of paper. All nodes are unlabeled and distinguishable. Each of you independently labeled the vertices from $1$ to $n$ . Neither of you know the other's labelling of the tree.

You and Li Chen each chose a subtree (i.e., a connected subgraph) in that tree. Your subtree consists of the vertices labeled $x_1, x_2, \ldots, x_{k_1}$ in your labeling, Li Chen's subtree consists of the vertices labeled $y_1, y_2, \ldots, y_{k_2}$ in his labeling. The values of $x_1, x_2, \ldots, x_{k_1}$ and $y_1, y_2, \ldots, y_{k_2}$ are known to both of you.

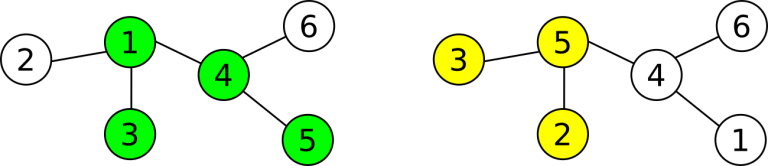The picture shows two labelings of a possible tree: yours on the left and Li Chen's on the right. The selected trees are highlighted. There are two common nodes.You want to determine whether your subtrees have at least one common vertex. Luckily, your friend Andrew knows both labelings of the tree. You can ask Andrew at most $5$ questions, each of which is in one of the following two forms:

• A x: Andrew will look at vertex $x$ in your labeling and tell you the number of this vertex in Li Chen's labeling.
• B y: Andrew will look at vertex $y$ in Li Chen's labeling and tell you the number of this vertex in your labeling.

Determine whether the two subtrees have at least one common vertex after asking some questions. If there is at least one common vertex, determine one of your labels for any of the common vertices.

思路

我们定义我的树为 $A$ 树，对方的树为 $B$ 树，如下图所示：

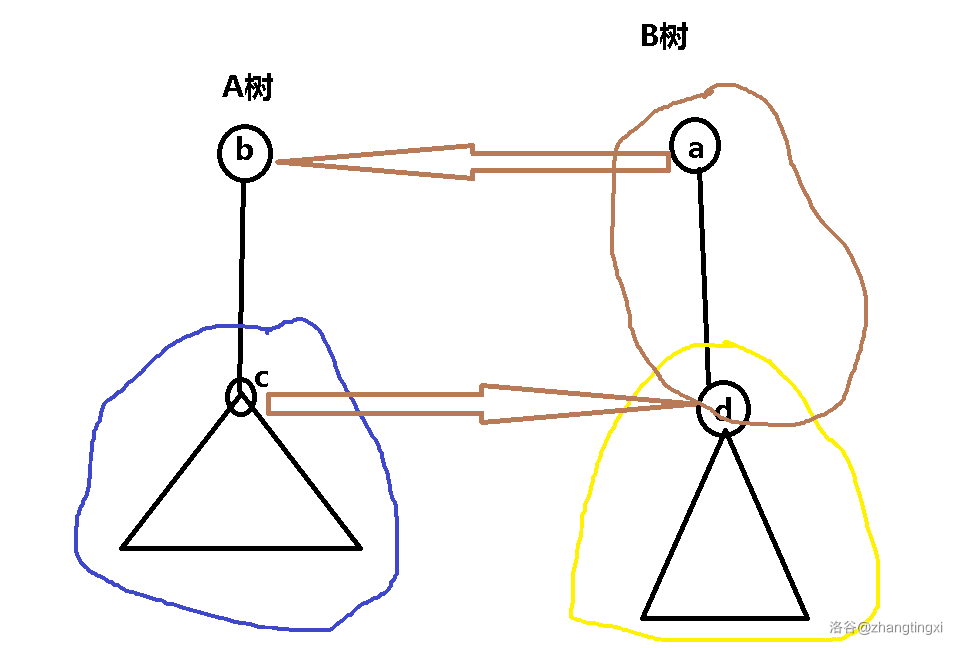
我们先取 $B$ 树中选了的其中一个点，假设为 $a$，询问它在 $A$ 树中的编号，记为 $b$。

假如 $b$ 就是 $A$ 中选了的点，输出 $b$ 即可。

否则，在 $A$ 树中以 $a$ 为根，则 $A$ 中 选了的 点应如蓝色区域所示，对应 $B$ 树中应为黄色区域。

设蓝色区域的根为 $c$ 点，询问其在 $B$ 中对应的点 $d$。因为选的点是连通块，所以 $B$ 中选了的点必然为红色区域，此时只需判断 $d$ 是否为 $B$ 中选中的点即可。

每组数据询问次数两次，总时间复杂度 $O(nT)$。

Code

// Problem: CF1044B Intersecting Subtrees
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF1044B
// Memory Limit: 250 MB
// Time Limit: 2000 ms

#include<bits/stdc++.h>
using namespace std;
//#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define N 10010
//#define M
//#define mo
struct node
{
	int x, y, n; 
}d[N<<1]; 
int n, m, i, j, k, T; 
int h[N], mx[N], my[N]; 
int a[N], b[N]; 
int u, v, x, y, k1, k2; 

void init()
{
	memset(h, 0, sizeof(h)); 
	memset(d, 0, sizeof(d)); 
	memset(mx, 0, sizeof(mx)); 
	memset(my, 0, sizeof(my)); 
	k=0; 
}

void cun(int x, int y)
{
	d[++k].x=x; d[k].y=y; 
	d[k].n=h[x]; h[x]=k; 
}

int dfs(int x, int fa)
{
	int g, y, z; 
	for(g=h[x]; g; g=d[g].n)
	{
		y=d[g].y; 
		if(y==fa) continue; 
		if(mx[y]) return y; 
		z=dfs(y, x); 
		if(z) return z; 
	}
	return 0; 
}

signed main()
{
//	freopen("tiaoshi.in","r",stdin);
//	freopen("tiaoshi.out","w",stdout);
	T=read(); 
	while(T--)
	{
		n=read(); init(); 
		for(i=1; i<n; ++i)
			u=read(), v=read(), cun(u, v), cun(v, u); 
		k1=read(); for(i=1; i<=k1; ++i) mx[a[i]=read()]=1; 
		k2=read(); for(i=1; i<=k2; ++i) my[b[i]=read()]=1; 
		printf("B %d\n", b[1]); 
		fflush(stdout); 
		cin>>x; if(x==-1) break; 
		// printf("%d\n", x); 
		if(mx[x]) printf("C %d\n", x), fflush(stdout); 
		else
		{
			y=dfs(x, 0); 
			printf("A %d\n", y); 
			fflush(stdout); 
			cin>>x; if(x==-1) break; 
			printf("C %d\n", (my[x] ? y : -1)); 
			fflush(stdout); 
		}
	}
	return 0;
}