【CF431C k-Tree】题解

题目链接

题目

Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a $ k $ -tree.

A $ k $ -tree is an infinite rooted tree where:

• each vertex has exactly $ k $ children;
• each edge has some weight;
• if we look at the edges that goes from some vertex to its children (exactly $ k $ edges), then their weights will equal $ 1,2,3,...,k $ .

The picture below shows a part of a 3-tree.

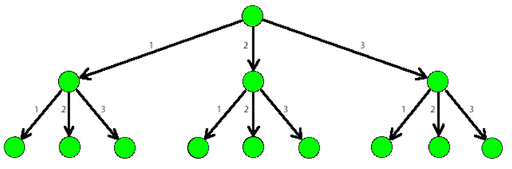
As soon as Dima, a good friend of Lesha, found out about the tree, he immediately wondered: "How many paths of total weight $ n $ (the sum of all weights of the edges in the path) are there, starting from the root of a $ k $ -tree and also containing at least one edge of weight at least $ d $ ?".Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo $ 1000000007 $ ( $ 10^{9}+7 $ ).

最近有一个富有创造力的学生Lesha听了一个关于树的讲座。在听完讲座之后，Lesha受到了启发，并且他有一个关于k-tree（k叉树）的想法。
k-tree都是无根树，并且满足：

1. 每一个非叶子节点都有k个孩子节点；
2. 每一条边都有一个边权；
3. 每一个非叶子节点指向其k个孩子节点的k条边的权值分别为1,2,3,...,k。

---

当Lesha的好朋友Dima看到这种树时，Dima马上想到了一个问题：“有多少条从k-tree的根节点出发的路上的边权之和等于n，并且经过的这些边中至少有一条边的边权大于等于d呢?”
现在你需要帮助Dima解决这个问题。考虑到路径总数可能会非常大，所以只需输出路径总数 mod 1000000007 即可。（1000000007=10^9+7）

思路

记忆化搜索。

我们另 \(dfs(x, y)\) 表示当前边权和为 \(x\)，最大权为 \(y\) 的方案数。

然后改成倒搜后显然其不存在后效性，固可以改成记忆化即可。

记录为两维，每次搜索有 \(k\) 个可能，时间复杂度为 \(O(n^3)\)。

可以把第二维优化成01两种状态，优化至 \(O(n^2)\)。但我没写

Code

// Problem: CF431C k-Tree
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF431C
// Memory Limit: 250 MB
// Time Limit: 1000 ms

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define N 110
//#define M
#define mo 1000000007
int n, m, i, j, k, T; 
int d; 
int f[N][N]; 

int dfs(int x, int y)
{
	if(x>n) return 0; 
	if(x==n && y>=d) return 1; 
	if(f[x][y]!=-1) return f[x][y]; 
	f[x][y]=0; 
	for(int i=1; i<=k; ++i)
		f[x][y]+=dfs(x+i, max(i, y)), f[x][y]%=mo; 
	return f[x][y]; 
}

signed main()
{
//	freopen("tiaoshi.in","r",stdin);
//	freopen("tiaoshi.out","w",stdout);
	memset(f, -1, sizeof(f)); 
	n=read(); k=read(); d=read(); 
	printf("%lld", dfs(0, 0)); 
	return 0;
}

总结

对于此类一眼没有思路或者觉得是恶心组合数学推式子的题目，可以先想一下打暴力dfs。

尝试观察暴力后是否有后效性，然后改成倒搜或加记忆化。