NOIP2021 题解(T1-T3)
我太弱了,改不出T4,就把T1-3题解码了。
T1 报数
题目链接
想着T2,T3的题解都写了,就补一下T1的吧。
典型的筛法。
假如一个数含有7,则把它的倍数全筛走。
这里可以加一个小优化,假如这个数已经被筛过,就不需要再筛它的倍数了。
最后再倒着预处理每个数的下一个没被筛的是什么。
如果不预处理,不断6999999就可以卡死你。
Code
#include<bits/stdc++.h>
using namespace std;
//#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();
}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();}return x*f;}
//#define M
//#define mo
#define N 10000050
int n, m, i, j, k;
int f[N], s[N], t, x;
int pan(int x)
{
while(x)
{
if(x%10==7) return 1;
x/=10;
}
return 0;
}
signed main()
{
// freopen("number.in", "r", stdin);
// freopen("number.out", "w", stdout);
for(i=1; i<=10000005; ++i)
{
if(pan(i))
{
if(!f[i])
for(j=i; j<=10000005; j+=i) f[j]=1;
}
// if(!f[i]) printf("%d\n", i);
}
for(i=10000005; i>=1; --i)
{
if(!f[i]) s[i]=i;
else s[i]=s[i+1];
// printf("s[%d]=%d\n", i, s[i]);
}
t=read();
while(t--)
{
x=read();
if(f[x]) printf("-1\n");
else printf("%d\n", s[x+1]);
}
return 0;
}
T2 数列
题目链接
首先dp得从低位向高位枚举,因为高位无论如果使用 都对低位二进制1的个数无影响,满足dp的无后效性。
设 为 从低的高二进制的前 位中,用了数列 的前 项,且此时 中共有 个二进制位为1,第 位进了 过去。
则:
假设这一位有 个 满足 ,则下一位就有 个 的元素确定,如果这一位是1,则 ,在转移中的 体现。而进位到下一位的就是 了。
对于每种方案,其对于答案的贡献为 ,而方案相当于在 个数中插 块板,即 。
建议用记忆化搜索实现。
Code
// Problem: P7961 [NOIP2021] 数列【民间数据】
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7961
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define mo 998244353
#define N 40
#define M 110
int n, m, i, j, k;
int c[M][M], s[M][M];
int f[M][N][N][N], v[M], K;
int count(int x)
{
int ans=0;
while(x) x-=x&-x, ++ans;
return ans;
}
int dfs(int k, int u, int x, int y)
{
if(u==n)
{
// printf("> f[%lld][%lld][%lld][%lld]=%lld\n", k, u, x, y, x+count(y)<=K);
if(x+count(y)>K) return 0;
// printf("----------");
return 1;
}
if(k>m) return 0;
if(f[k][u][x][y]!=-1) return f[k][u][x][y];
int ans=0;
for(int i=0; i<=n-u; ++i)
{
ans=(ans+dfs(k+1, u+i, x+((y+i)&1), (y+i)>>1)
*s[k][i]%mo*c[u+i][i]%mo)%mo;
// printf("%lld %lld\n", s[k][i], c[n-u][i]);
}
f[k][u][x][y]=ans;
// printf("f[%lld][%lld][%lld][%lld]=%lld\n", k, u, x, y, f[k][u][x][y]);
return f[k][u][x][y];
}
signed main()
{
// freopen("tiaoshi.in","r",stdin);
// freopen("tiaoshi.out","w",stdout);
memset(f, -1, sizeof(f));
n=read(); m=read(); K=read();
for(i=0; i<=m; ++i) v[i]=read();
c[0][0]=1;
for(i=1; i<=n; ++i)
for(j=c[i][0]=1; j<=i; ++j)
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mo;
for(i=0; i<=m; ++i)
{
s[i][0]=1;
for(j=1; j<=n; ++j) s[i][j]=(s[i][j-1]*v[i])%mo;
}
printf("%lld\n", dfs(0, 0, 0, 0));
return 0;
}
T3 方差
题目链接
Part A 式子化简
首先题目要求的式子就是 乘上 ,其中 。
我们把这三合在一起也就是:
前面化简一下,后面用完全平方公式展开:
拆开:
对于第二坨,把与 无关的抽出来:
把第二坨化简一下:
把第二坨的后两个写成平方的形式:
看第三坨,发现没有和 有关的项,之间把 变成乘 :
化简一下第三坨:
然后我们发现二、三坨可以合并:
于是对于每种 我们都有直接算的方法了。
Part B 差分交换
现在让我们考虑令一个问题。
对于相邻的三个数 、、,我们计算相邻两数的差分别为 、。
先在我们把 变成 ,现在就是 、、。
然后我们再对相邻两数作差分别为:、。
发现了什么?
没错,我们对每个数进行交换,只不过是把相邻两项的差交换。
于是我们对 作差分序列 ,这样无论我们对 序列进行怎样的变换, 序列的元素始终不变,只是顺序改变。
基于这个结论,我们可以枚举 的顺序,时间复杂度 。
Part C 差分单谷性
这里我们可以引出一个结论: 的排列必然是先从大到小,再从小到大。
这里可以感性理解一下,因为对于每个 只有不断靠近平均数,方差才最小。
我们也可以大致运用反证法证明。(有误请指出)
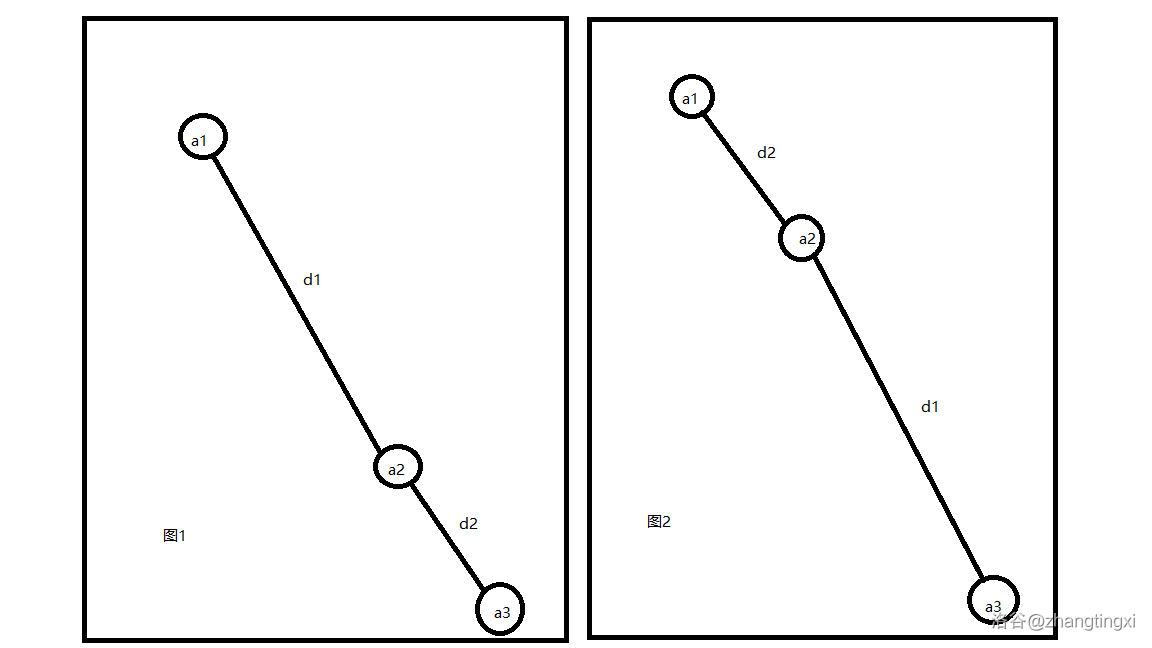
图中 ,我们发现 与 的值不变,图2相比图1中只有 变大了。
两个 相比,显然图1中的 更靠近谷底,也就是 。按照开始的式子 我们发现 取图1的情况更优。
有了这个结论,我们可以把 按从大到小排序,对于 ,要么放左边,要么放右边,通过此方法,我们就得到了一种 的暴力。
48分Code
// Problem: P7962 [NOIP2021] 方差【民间数据】
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7962
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
// #define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define N 410
//#define mo
int n, m, i, j, k;
int a[N], d[N], b[N];
int ans=0x7fffffff;
int sum, num;
bool cmp(int x, int y)
{
return x>y;
}
void dfs(int x, int l, int r, int s, int t)
{
if(l==r-1)
{
ans=min(ans, n*t-s*s);
return ;
}
int k;
k=a[l+1]=a[l]+d[x]; dfs(x+1, l+1, r, s+k, t+k*k);
k=a[r-1]=a[r]-d[x]; dfs(x+1, l, r-1, s+k, t+k*k);
}
signed main()
{
// freopen("tiaoshi.in","r",stdin);
// freopen("tiaoshi.out","w",stdout);
n=read();
for(i=1; i<=n; ++i) a[i]=read();
for(i=2; i<=n; ++i) d[i-1]=a[i]-a[i-1];
sort(d+1, d+n, cmp);
dfs(1, 1, n, a[1]+a[n], a[1]*a[1]+a[n]*a[n]);
printf("%d", ans);
return 0;
}
Part D 相对位置代替绝对位置
可以发现,我们在上面的方法中每次都把 的绝对位置求出来。但其实我们可以只求出其相对位置。
我们先对 从小到达排序,再一条一条放进去。此时 的位置是在这种放进去的方法下的 。
首先让我们把之前的式子搬回出来:
我们要让结果最小,就是要让 最大, 最小。
让我们设 表示已经决定的 个 里面,和为 的最小平方和。设 为当前的 的 。
可以理解为 , 可以理解为 。
现在对于 ,要么放在左边,要么放在右边。
先说放在右边, 则会加上当前点的坐标,答案加上当前的平方,而当前点为 。
放在左边的话,就是整体 右移 , 就明显是加上 ,至于 的话,这里要手推一下。
首先至少要加上这个点 ,然后后面的和变成 ,而原先是 ,所以加上的是:
前面用完全平方公式拆一下:
最前面与最后面两坨消去:
前面那坨把无关紧要的提出了:
把 套进去:
后面那坨直接把 变成乘 :
根据这个,我们可以把放左边的dp推出了:
后面两个合一下:
然后就行了。
转移方程与最终代码可能有一些细节的东西,改一改就行了。
可是按照这个方法打只有72分。
72分code
// Problem: P7962 [NOIP2021] 方差【民间数据】
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7962
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define N 410
#define M 610
//#define mo
int n, m, i, j, k;
int a[N], d[N];
int ans=0x7fffffffff;
int sum, num;
int f[N][N*M];
signed main()
{
// freopen("tiaoshi.in","r",stdin);
// freopen("tiaoshi.out","w",stdout);
n=read();
for(i=1; i<=n; ++i) a[i]=read();
for(i=2; i<=n; ++i) d[i-1]=a[i]-a[i-1];
sort(d+1, d+n);
for(i=0; i<=n; ++i) for(j=0; j<=240000; ++j) f[i][j]=ans;
f[0][0]=0;
for(i=0; i<n-1; ++i)
{
sum+=d[i+1];
for(j=0; j<=240000; ++j)
{
f[i+1][j+sum]=min(f[i+1][j+sum], f[i][j]+sum*sum);
f[i+1][j+d[i+1]*(i+1)]=min(f[i+1][j+d[i+1]*(i+1)], f[i][j]+2*j*d[i+1]+(i+1)*d[i+1]*d[i+1]);
// if(f[i][j]!=ans)
// printf("f[%lld][%lld]=%lld\n", i, j, f[i][j]);
}
}
for(i=0; i<=24000; ++i)
{
// if(f[n-1][i]!=0x7fffffffff) printf("f[%lld][%lld]=%lld\n", n-1, i, f[n-1][i]);
// ans=min(ans, n*(f[n-1][i]+2*i*a[1]+(n-1)*a[1]*a[1]+a[1]*a[1])-(a[1]*n+i)*(a[1]*n+i));
ans=min(ans, n*f[n-1][i]-i*i);
}
printf("%lld", ans);
return 0;
}
Part E 小优化
我们发现主要是集中在MLE和TLE。
MLE方面,我们可以使用滚动数组。
TLE的话,对于 的循环范围,我们可以动态分配。
提一句,最后加不加上 都行(实测可以)。
最后贴上AC code:
// Problem: P7962 [NOIP2021] 方差【民间数据】
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P7962
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;
ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+
(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define N 10010
#define M 610
//#define mo
int n, m, i, j, k;
int a[N], d[N];
int ans=0x7ffffffffff;
int sum, num, p, q;
int f[2][500010];
signed main()
{
// freopen("tiaoshi.in","r",stdin);
// freopen("tiaoshi.out","w",stdout);
n=read();
for(i=1; i<=n; ++i) a[i]=read();
for(i=2; i<=n; ++i) d[i-1]=a[i]-a[i-1];
sort(d+1, d+n);
for(j=0; j<=500000; ++j) f[1][j]=f[0][j]=ans;
f[0][0]=0;
for(i=0; i<n-1; ++i)
{
sum+=d[i+1];
p=(i+1)%2; q=i%2; num+=d[i+1]*(i+1);
for(j=0; j<=num; ++j) f[p][j]=ans;
for(j=0; j<=num; ++j)
{
if(j+sum<=num)
f[p][j+sum]=min(f[p][j+sum], f[q][j]+sum*sum);
if(j+d[i+1]*(i+1)<=num)
f[p][j+d[i+1]*(i+1)]=min(f[p][j+d[i+1]*(i+1)], f[q][j]+2*j*d[i+1]+(i+1)*d[i+1]*d[i+1]);
}
}
for(i=0; i<=500000; ++i)
{
//ans=min(ans, n*(f[(n-1)%2][i]+2*i*a[1]+(n-1)*a[1]*a[1]+a[1]*a[1])-(a[1]*n+i)*(a[1]*n+i));
//可写可不写,是是否加上a1的情况
ans=min(ans, n*f[n-1][i]-i*i);
}
printf("%lld", ans);
return 0;
}
本文来自博客园,作者:zhangtingxi,转载请注明原文链接:https://www.cnblogs.com/zhangtingxi/p/15600134.html




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 浏览器原生「磁吸」效果!Anchor Positioning 锚点定位神器解析
· 没有源码,如何修改代码逻辑?
· 一个奇形怪状的面试题:Bean中的CHM要不要加volatile?
· [.NET]调用本地 Deepseek 模型
· 一个费力不讨好的项目,让我损失了近一半的绩效!
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战