manacher 算法总结

测试一下这个博客园的功能（图片好像只能在洛谷上看，有时间就改）

manacher 算法总结

题目大意

给定一字符串，求其最长回文串长度

方法对比

暴力效率：$O(n^3)$，优化后为$O(n^2)$

manacher效率：$O(n)$

算法思想

回文串有两种：奇回文与偶回文

分类讨论太麻烦，主要是我不会，于是我们就统一为奇回文

如何统一

例：

abbab

偶回文：abba 奇数回文：bab

我们在中间各插入一个符号，例如#号

则原式变为：

#a#b#b#a#b#

此时奇回文还是已某个子母为中心的回文，如：

bab->#b#a#b#

此时这个回文仍以a为中心

通过观察可以发现，偶回文变成已#为中心的奇回文，如：

abba->#a#b#b#a#

此时这个回文已第三个#号为中心

我们把原先的串命名为 $s$ 串，修改后的串命名为 $t$ 串，定义数组 $p$

$p[i]$ 表示在 $t$ 串中以 $i$ 为中心最多能扩散的半径（包括 $i$ 本身）

例如：

t: # a # b # b # a # b #
p: 1 2 1 2 5 2 1 4 1 2 1

可是此时 $t$ 与 $s$ 不同，怎么通过 $p$ 来还原长度呢？

还原长度

先上结论：最长回文长度 $ans$ 为

$ans=MAX^{i-1}_n(p[i]-1)$

为什么是 $p[i]-1$ 呢？

如果是奇回文：

#b#c...#b#a#b...c#b#

右边每一个字母都可以与对应左边字母的右边#消除

最后剩下最左边的#，所以为 $p[i]-1$

如果是偶回文：

#b#c...d#a#a#a#d...c#b#

按照奇回文的思路我们也可以得到 $p[i]-1$ 这个结论，这里可以再自己手动推一下

现在大致思路是这样，可是怎么求 $p[i]$ 呢，这是manacher精粹之一

对称思维

我们首先假设我们进行到 $p[i]$, 且 $p[1...i-1]$ 已知

则前面 $p[1...i-1]$ 必存在一个 $p[id]$，使得 $p[id]+id$ 最大，记为 $mx$

即：$mx=MAX^{id=1}_{i-1}(p[id]+id)$

注意，$id$ 可以为 $1$ 到 $i-1$ 任意一位置

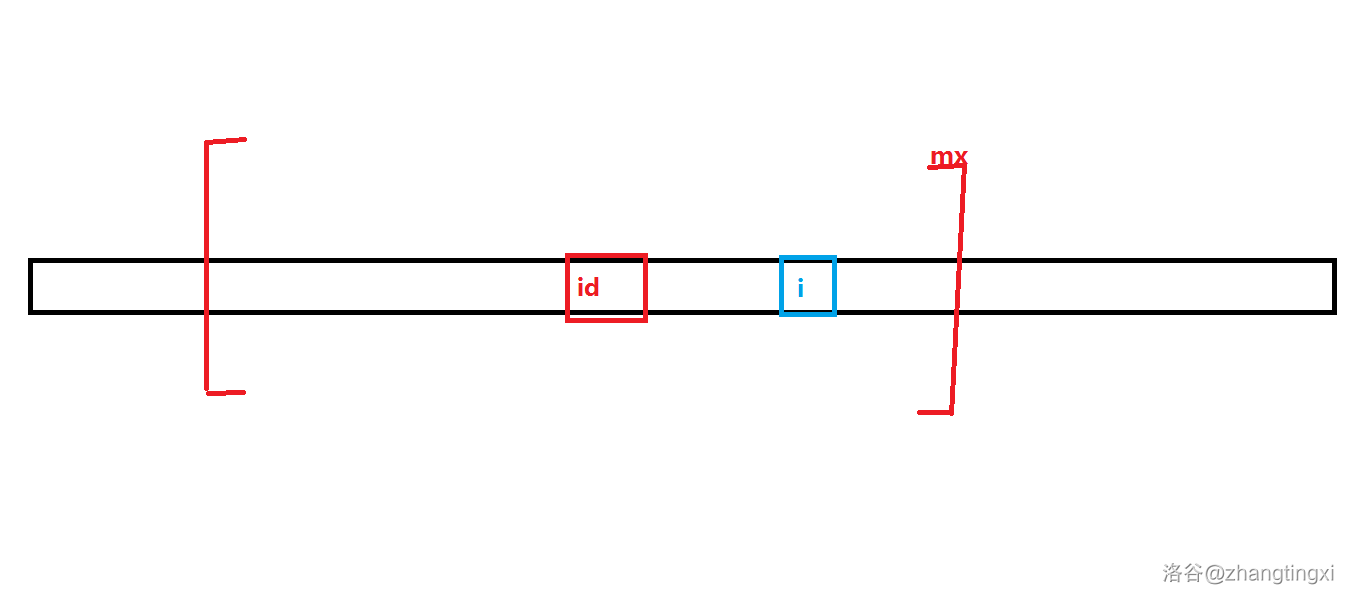
图中黑色矩形为 $t$ 串，蓝色矩形代表子母 $i$，红色矩形代表子母 $id$，红色框架代表已 $id$ 为中心的最长回文串，其中右边界记为 $mx$

同时，以 $id$ 为原点两边会出现对称情况，所以 $i$ 必然会出现其对称点 $i'$

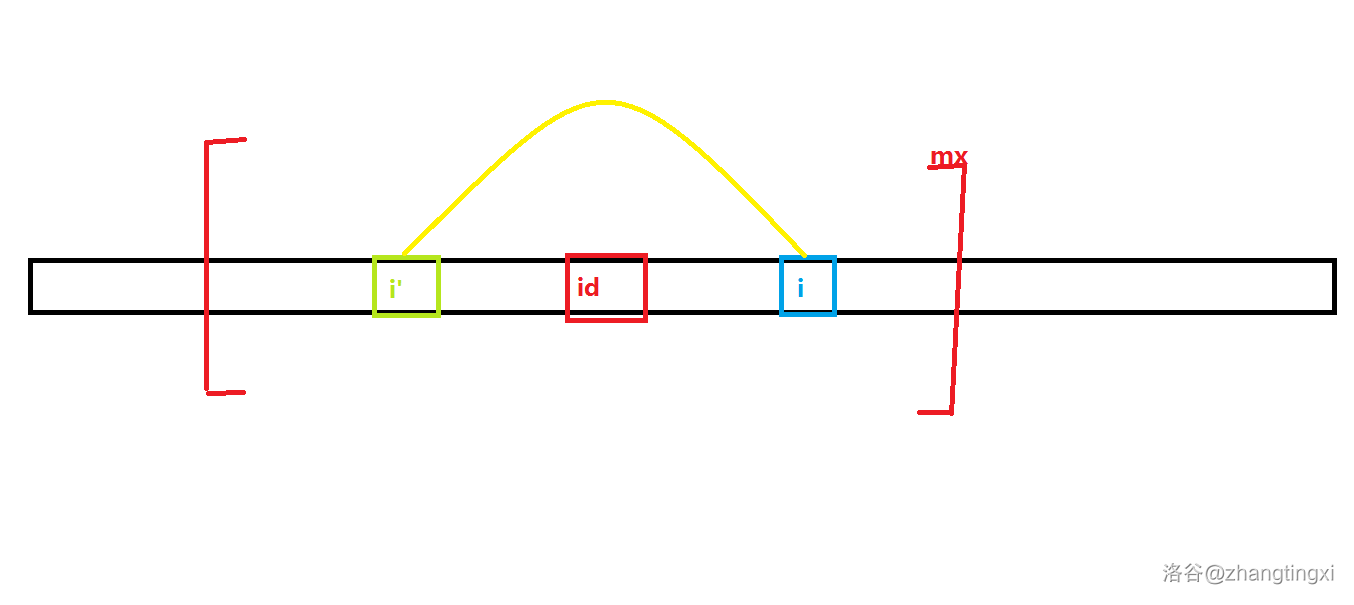
图中绿色矩形代表与蓝色矩形 $t[i]$ 相等且围绕 $id$ 对称的子母 $t[i']$, 黄色线代表两点对称

此处直接给出i'的公式，有时间可以自己证

$i'=2\times id-i$

具体是运用了原点对称的思想

此时 $i'$ 也必然有自己的管辖范围(即以 $i'$ 为中心的最长回文长度)，我们分两种情况讨论

情况1：$i'$ 管辖范围在 $id$ 的管辖范围以内

则：$p[i]=p[i']$

因为此时 $i'$ 的管辖范围必然与i的管辖范围以 $id$ 为原点一一对称，详见图：

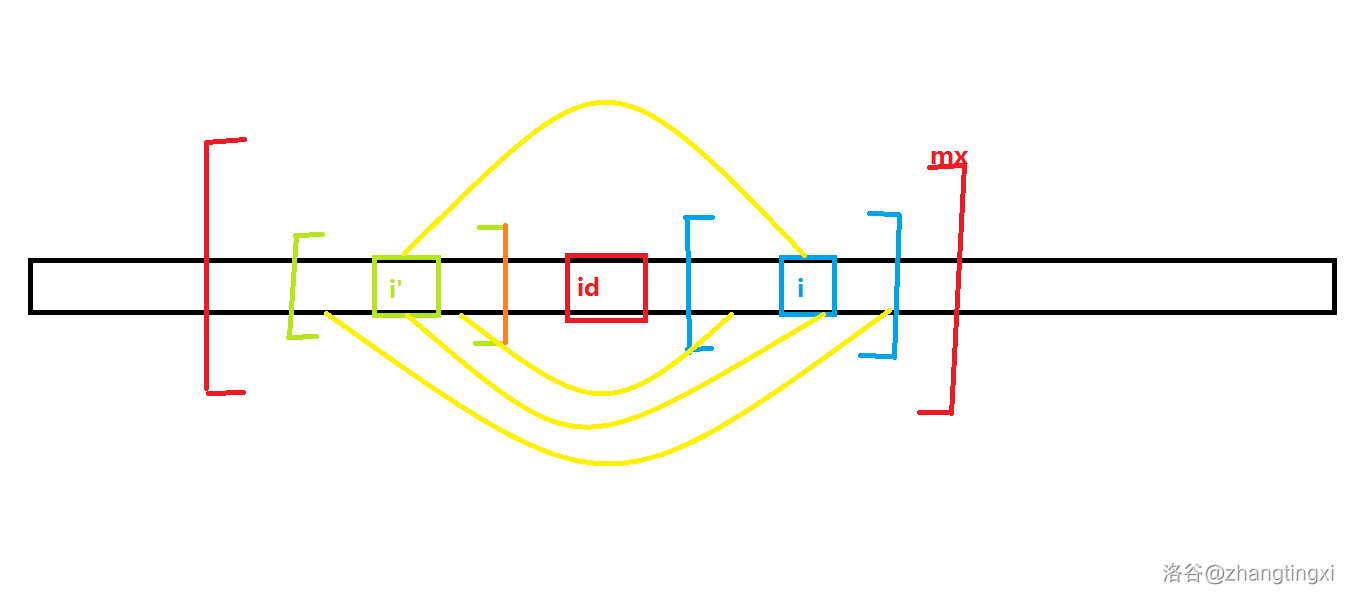
图中绿色框架代表 $i'$ 管辖范围，蓝色框架代表 $i$ 管辖范围，下面的黄色线代表绿色框架与蓝色框架以 $id$ 为中心的一一对应

情况2：$i'$ 管辖范围不在 $id$ 管辖范围以内

则首先，$p[i]$ 至少为 $p[i]=mx-i$

那么超出部分（紫色部分）怎么办呢，暴力呗

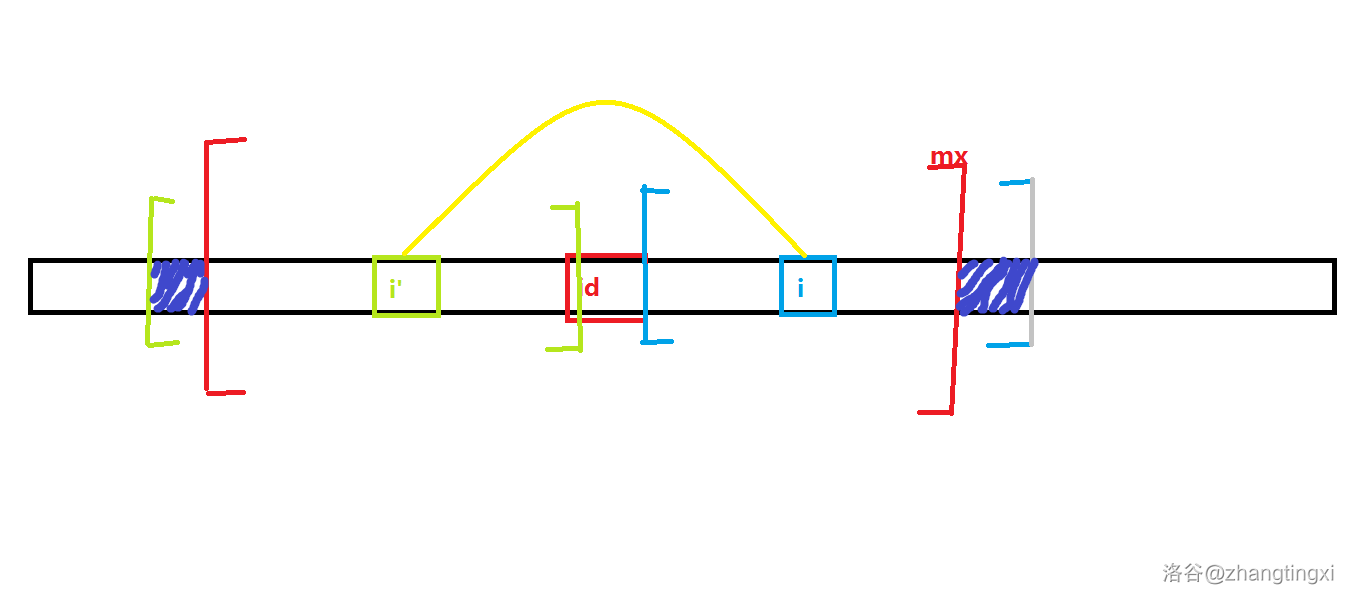
图中紫色区域代表超出部分

此时我们就可以处理所有 $p[i]$ 了

边界问题

可以看出，我们再求 $2\times id-i$ 和 $mx-i$ 时可能越出左边界

求紫色区域时可能越出右边界，则我们在 $t$ 串左右分别加上两个字符，例如+和-

核心思路大致如此

核心代码

	for(int i=1;i<=n;++i)
	{
		p[i]=1;
		if(i<=mx)
			p[i]=min(p[2*id-i],mx-i);
		while(t[i-p[i]]==t[i+p[i]])
			++p[i];
		if(i+p[i]>mx)
			id=i,mx=i+p[i];
	}

效率分析

双重循环，看起来是$O(n^2)$，但事实上每次进入while循环，$mx$ 值必改变，而 $mx$ 值最大为 $n$，所以时间效率为$O(n)$(不考虑常数)

完整代码

#include<bits/stdc++.h>
using namespace std;
char s[11000010];
char t[25000010];
int p[25000010];
int l,mx,id,ans;

int main()
{
//	freopen("tiaoshi.in","r",stdin);
//	freopen("tiaoshi.out","w",stdout);
	scanf("%s",s+1);
	t[0]='+';
	l=1;
	for(int i=1;s[i];++i,++l)
	{
		t[l]='#';
		t[++l]=s[i];
	}
	t[l]='#';
	t[l+1]='-';
	for(int i=1;i<=l;++i)
	{
//		printf("%c",t[i]);
		p[i]=1;
		if(i<=mx)
			p[i]=min(p[2*id-i],mx-i);
		while(t[i-p[i]]==t[i+p[i]])
			++p[i];
		if(i+p[i]>mx)
			id=i,mx=i+p[i];
		ans=max(ans,p[i]);
	}
//	printf("\n");
	printf("%d",ans-1);
	return 0;
}

参考代码2：

scanf("%s", c+1); n=strlen(c+1); 
s[0]='-'; s[1]='#'; 
for(i=1, j=2; i<=n; ++i, ++j) 
	s[j]=c[i], s[++j]='#'; 
s[j]='+'; n=j-1; r=0; 
for(i=1; i<=n; ++i)
{
	if(i>r) a[i]=2; 
	else a[i]=min(a[2*j-i], r-i+1); 
	while(s[i-a[i]]==s[i+a[i]]) ++a[i]; 
	if(i+a[i]-1>r) r=i+a[i]-1, j=i; 
	ans=max(ans, a[i]-1); 
}
printf("%d", ans);