Trie树的简单分析及极简实现
摘要:本文借助递归方式,用尽可能短的代码实现了Trie,重在讨论Trie的结构和思想,此方式实现的Trie效率较低,不能应用于实际工程中。
Trie的应用
trie: 发音为try,是一种应用于字符串查找的特殊查找表,首先介绍一下他的优点以及适用场景吧,实际上我们对于可能天天都在享受这项技术带来的便利,但却浑然不知,我贴上图,相信您就能立马明白:
该数据结构能够在常数级别判断数据库中所有以目标字符串为前缀的字符串。假如我们是用哈希表来存储我们的词表,显然是做不到的。
Trie的数据结构
总结来讲,trie是一种利用空间换时间的算法思想,对于每个节点,存储的是所有字符表的字符,用从根节点到叶节点的路径来指示存储内容,图形化表示如下:
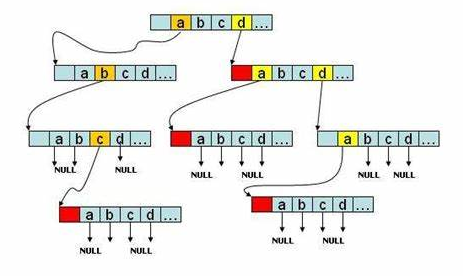
可以看出,假如Trie存储的内容不多的话,有大量的节点被浪费掉了,存储密度很低,十分浪费内存,当词表阅读,存储的单词越少,浪费的内存就越高。
Trie的实现
首选定义节点结构,采用递归定义的方式:
class Trie{
private Trie[] array;
//假设词表中仅存储小写单词
private static final int N = 26;
private boolean isEnd;
public Trie() {
array = new Trie[N];
isEnd = false;
}
}
//
首先来看查询代码,这里为了方便,我们采用递归的方式,我们假设当查询到单词结尾时,该路径不为空,那么 那么此时存在该单词,但是这样无法区分重叠路径的情况,假设Trie中存在apple这个单词,但是不存在app这个单词,尽管我们查询到最后,p指向的路径不为空,但是其实不存在这个单词,因此我们需要对这种情况加以区分。我们引入isEnd这个标志,把路径的结尾加上isEnd标志,这样就可以将这两种情况区分开来了。解决了递归出口问题,那么递归也很容易写了直接返回array[s.charAt(0)-'a'].search(s.substring(1))即可。代码如下,非常简单:
public boolean search(String word) {
if(word.length() == 0) return isEnd;
int idx = word.charAt(0) - 'a';
if(array[idx] == null) return false;
else return array[idx].search(word.substring(1));
}
既然能够写出search代码,那么很显然startWith这个函数也很容易实现,因为只要存在这条路径即可,不需要判断是否是叶节点,代码如下:
public boolean startsWith(String word) {
if(word.length() == 0) return true;
int idx = word.charAt(0) - 'a';
if(array[idx] == null) return false;
return array[idx].startsWith(word.substring(1));
}
同理,我们采用递归的方式插入代码,由于我们规定不准插入空字符串,那么递归出口便是当单词长度为1时,先看代码:
public void insert(String word) {
if(word.length() == 0) return;
int idx = word.charAt(0) - 'a';
if(array[idx] == null) array[idx] = new Trie();
if(word.length() != 1) {
array[idx].insert(word.substring(1));
}
else array[idx].isEnd = true;
}


