图机器学习task1:

task01:图机器学习导论

1.图技术的应用

• 一切皆可用图表示

2.图的分类

• 异质图（heterogeneous graph）：节点存在不同类型，连接也存在不同类型 (类型数大于等于2)

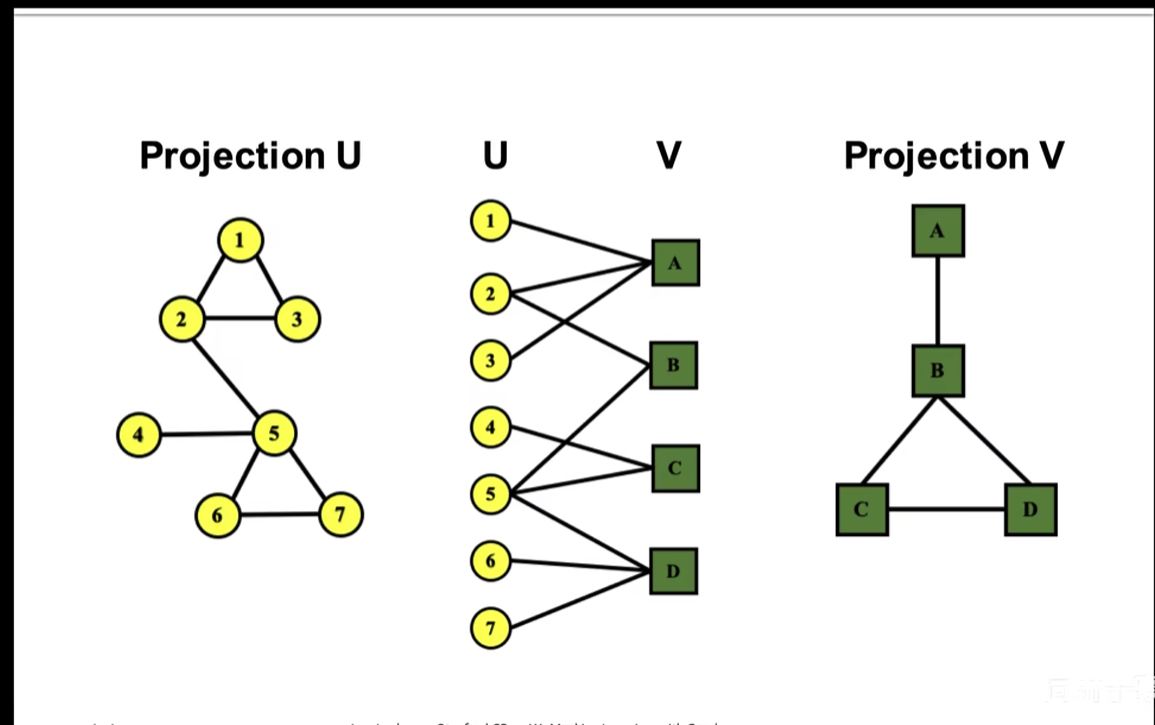
• 二分图（Bipartite graph）:只存在两类节点，比如：论文和作者，演员和电影，用户给和电影

  • 二分图展开：按U展开（都是同一类型节点，1，2，3都和A有关系，那么在，1，23，之间建立连接），按V展开（A,B都和2，有关系，所以A和B之间建立一条边）

3.图论中几个重要概念

• 节点连接数（Node degree）：一个节点存在多少个连接，那么这个节点的“度”就是多少

  一张图的平均节点连接数：总的节点数E乘以2，然后再除以节点个数N

  如果是有向边的话，那就需要再细分为in-degree和out-degree

  如果一个节点的in-degree等于0，那么它就是一个source；

  如果一个节点的out-degree等于0，那么他就是一个sink

  对于有向图的平均节点连接数：E/N in-degree的平均值会等于out-degree的平均值

• 图的基本表示：邻接矩阵（Adjacency Matrix）

  通俗一点说就是 “行指向列”，那个位置就是1，比如，2和4之间，第二行第四列就是2指向4，这里有边，所以矩阵的值就是1

  无向图的邻接阵一定是对称矩阵并且主对角线为0，有向图：非对称矩阵

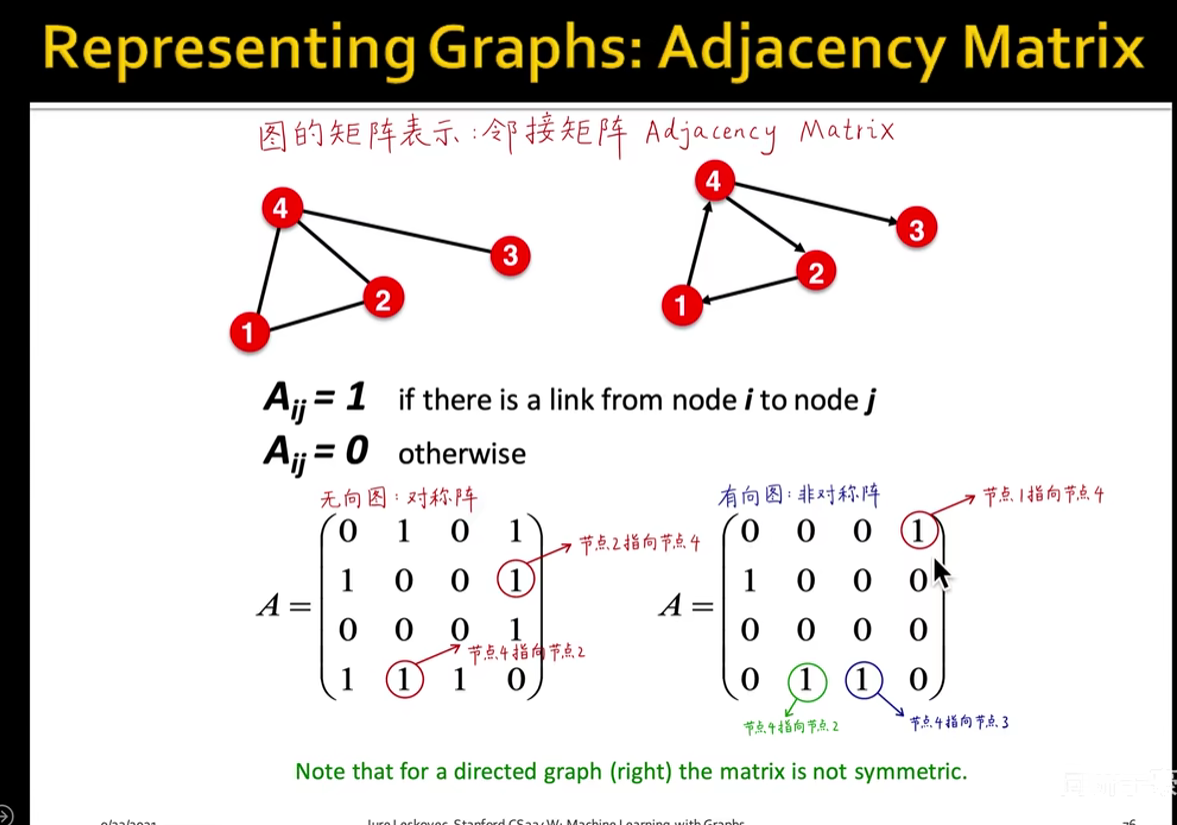
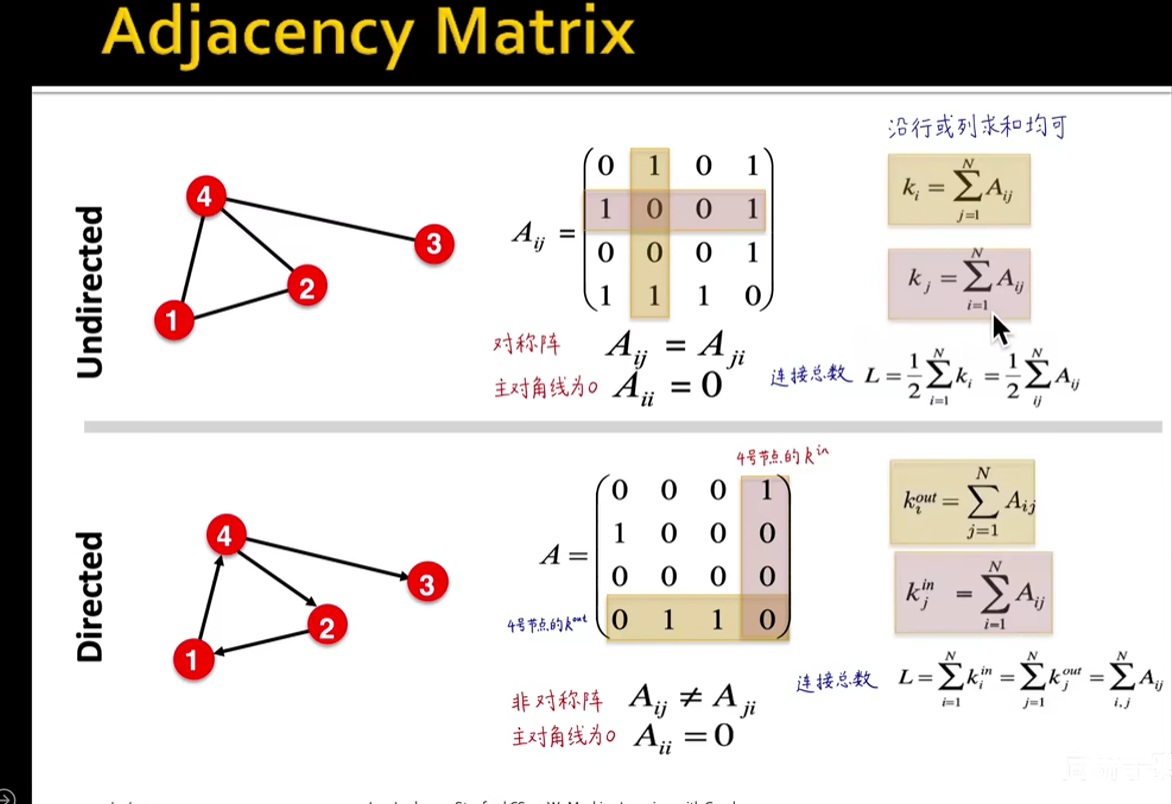
对于无向图，根据邻接图，求某一个节点的连接数：按行或者按列求和就可以了；

对于有向图，根据邻接图，求某一个节点的连接数：4号节点的in-degree是按行求和（即算第四列的总和）；out-degree是按列求和（即第四行的数的总和）

思考题：为什么把图表示成矩阵形式？

因为邻接矩阵保留了图的所有信息，它是全息的，把图翻译成计算机的语言

世界上大部分表示图的邻接矩阵都是稀疏矩阵，比如70亿人的社交网络图的邻接矩阵（70亿行，70亿列的矩阵），一个人认识的人不超过1000人，那么这个矩阵只有1000个1，所以是一个稀疏矩阵

• 图的基本表示：连接列表、邻接列表：以上如果图用邻接矩阵来表示的话，是一个非常稀疏的矩阵，会很占用内存，因此就得找新的方法来表示图，列表就出现了

  • 连接列表：只记录存在连接的节点（对）

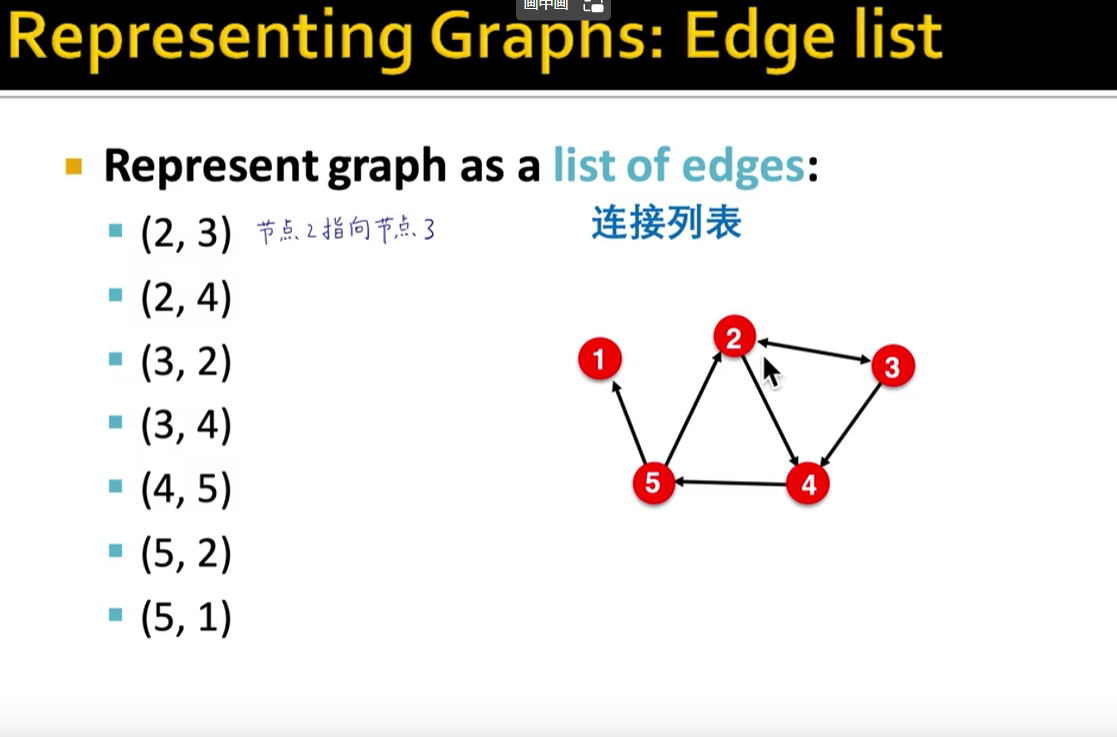
• 邻接列表：用一行表示一个节点，并且在这一行内，把该节点所有的指向信息标明

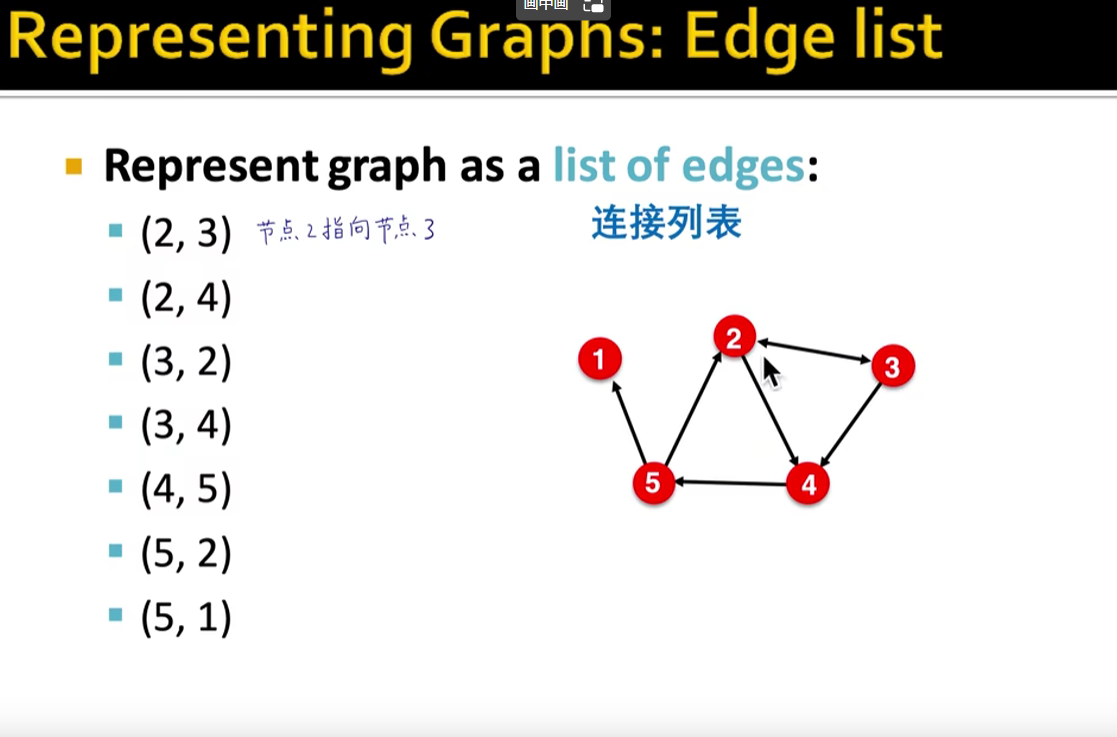
• 其他类型的图（带权重的图，比如道路的可通达性，社交人之间的关系）

  

  两个节点之间有多个关系：

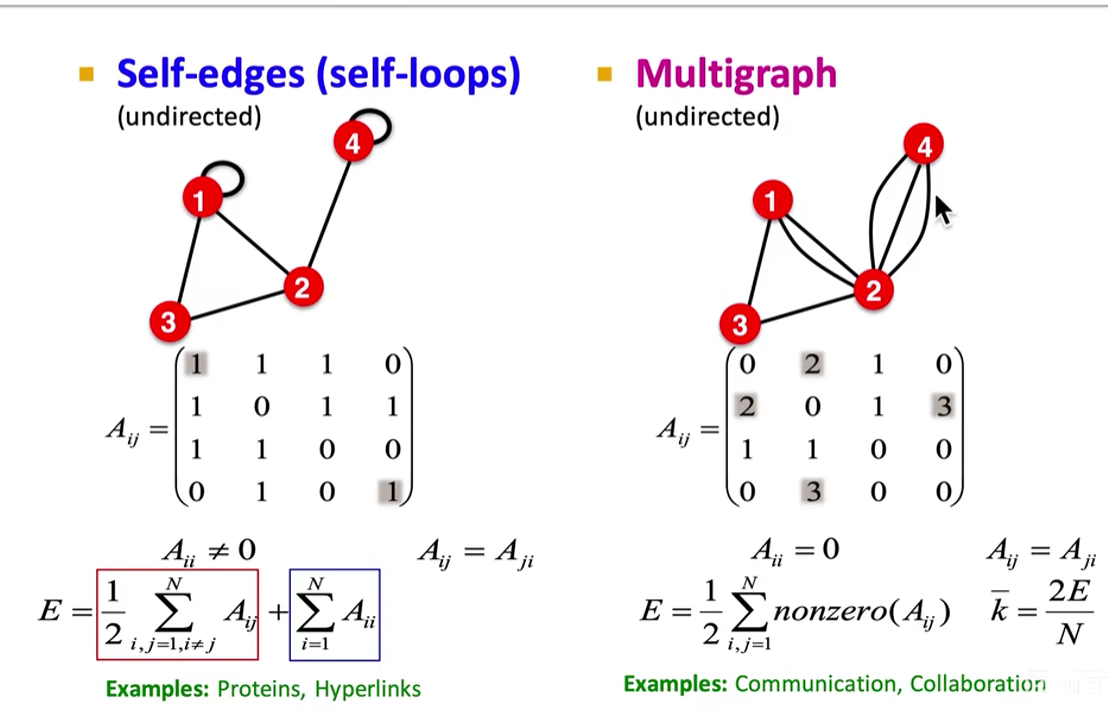
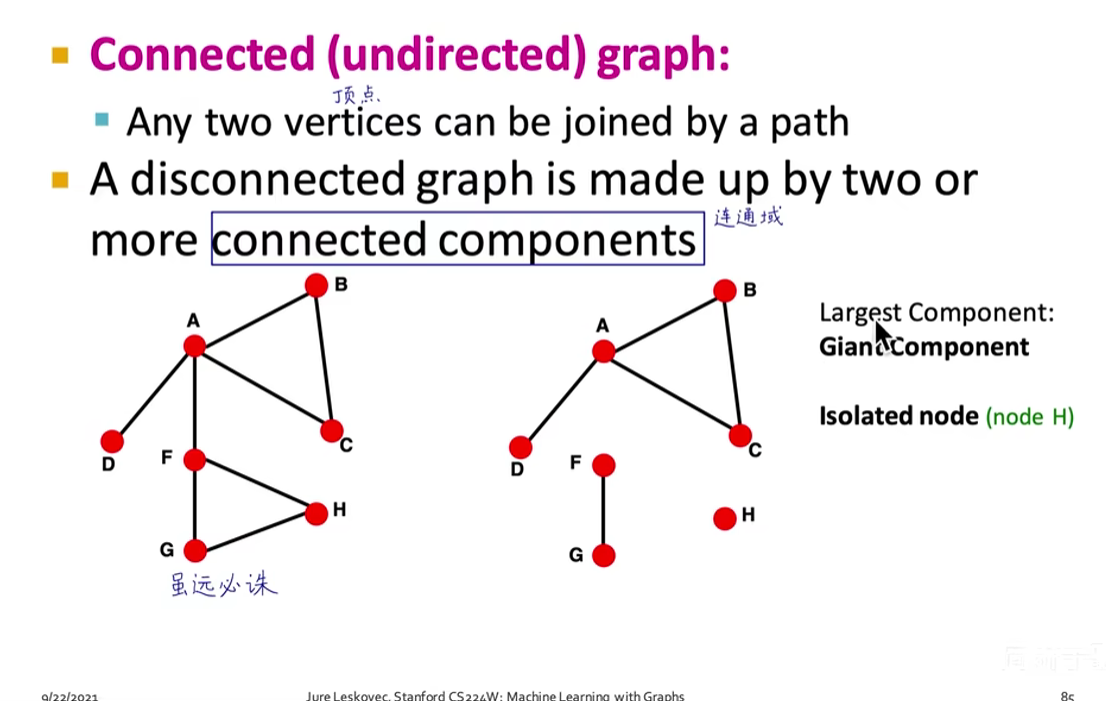
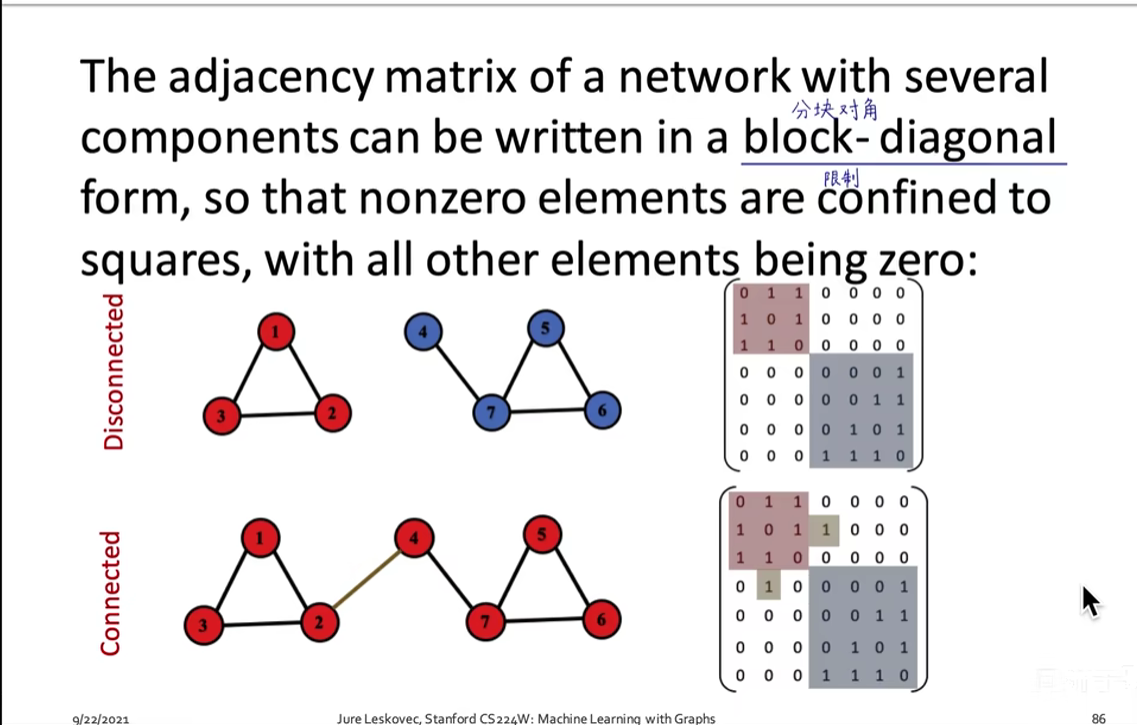
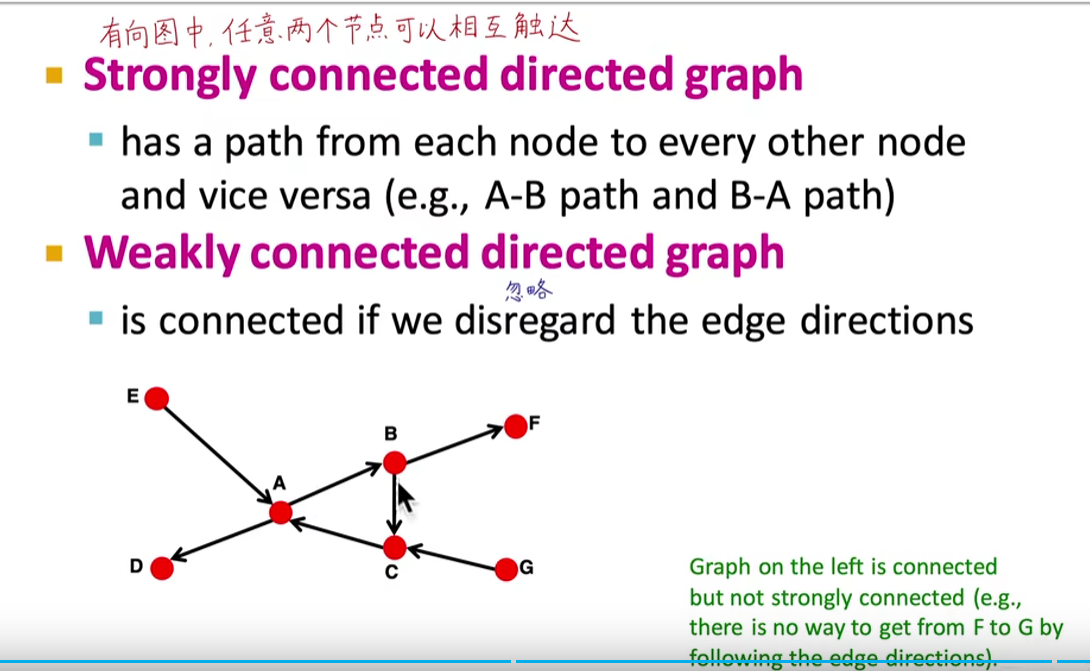
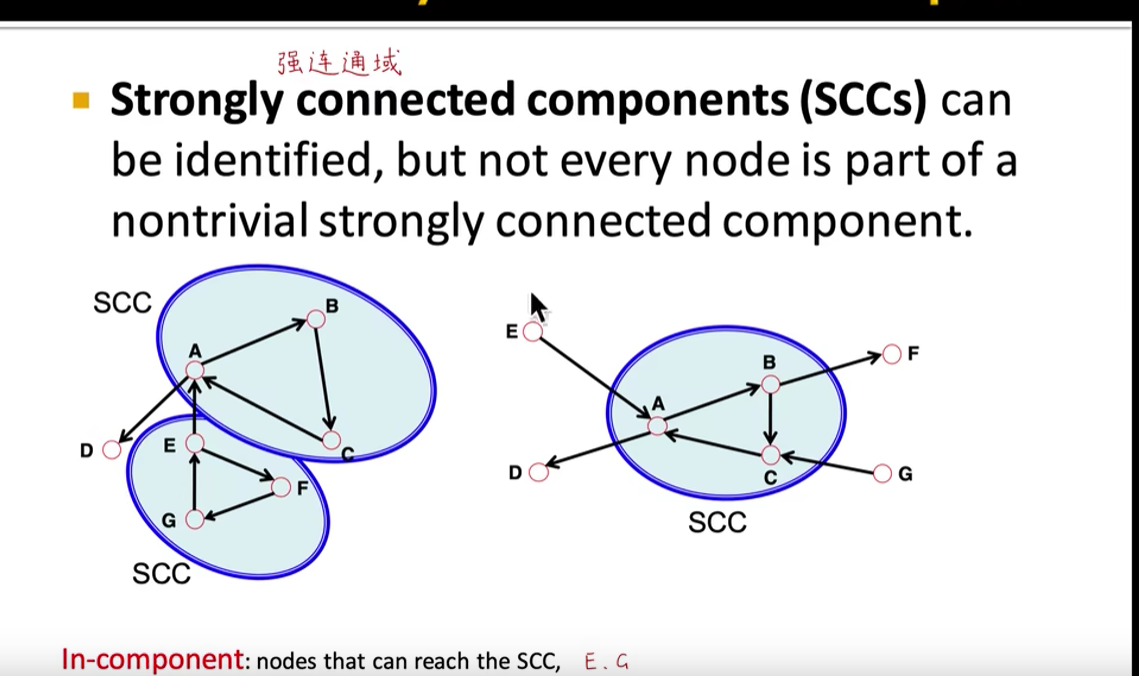
• 图的连通性