因子分析AF
一、概述
1.1 什么是因子分析
因子分析的起源是这样的,1904年英国的一个心理学家发现学生的英语、法语和古典语成绩非常有相关性,他认为这三门课程背后有一个共同的因素驱动,最后将这个因素定义为“语言能力”。基于这个想法,发现很多相关性很高的因素背后有共同的因子驱动,从而定义了因子分析。
因子分析在经济学、心理学、语言学和社会学等领域经常被用到,一般会探索出背后的影响因素如:语言能力、智力、理解力等。这些因素都是无法直接计算,而是基于背后的调研数据所推算出的公共因子。
因此概括下,因子分析就是将存在某些相关性的变量提炼为较少的几个因子,用这几个因子去表示原本的变量,也可以根据因子对变量进行分类。
1.2 解决什么问题
1. 在多变量场景下,挖掘背后影响因子
2. 用于数学建模前的降维
二、步骤
因子分析是寻找不线性相关的“变量”的线性组合来表示原始变量,这些“变量”称为因子,如下图中的F就是因子,X是原始变量,eps是原始变量不可被公共因子表示的部分。
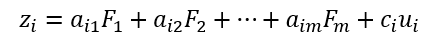
以上的公式还需要满足:
- 要求因子的数据小于原始变量的数量,即m≤p;
- 因子F之间是相互独立且方差为1;
- 因子F和eps之间的相关性为0,eps之间相关性为0。
因此,因子分析的过程就是实现以下几个目的的过程:
- 求解方程中的因子F的系数;
- 给予因子F实际的解释;
- 展示原始特征和公共因子之间的关系,从而实现降维和特征分类等目的。
1)充分性检验
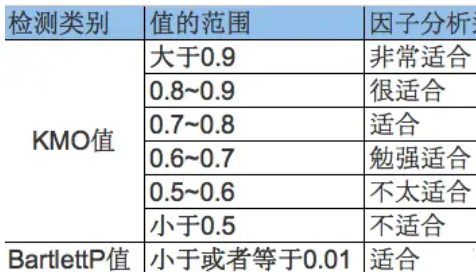
- 目的:检验变量之间是否存在相关性,从而判断是否适合做因子分析;
- 方法:抽样适合性检验(KMO检验)或者 巴特利特检验(Bartlett’s Test)。
2)选择因子个数
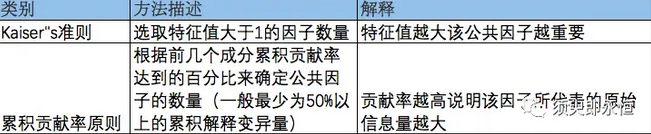
- 目的:通过数据定义最合适的潜在公共因子个数,这个决定后面的因子分析效果;
- 方法:Kaiser”s准则 或者 累积贡献率原则。
3)提取公共因子并做因子旋转
提取公共因子就是上面提到的求解函数的过程,一般求解方法有:主成分法、最大似然法、残差最小法等等。
因子旋转的原因是提取公共因子的解有很多,而因子旋转后因子载荷矩阵将得到重新分配,可以使得旋转后的因子更容易解释。常用的方法是方差最大法。
4)对因子做解释和命名
- 目的:解释和命名其实是对潜在因子理解的过程;这一步非常关键,需要非常了解业务才可。这也是我们使用因子分析的主要原因。
- 方法:根据因子载荷矩阵发现因子的特点。
5)计算因子得分
对每一样本数据,得到它们在不同因子上的具体数据值,这些数值就是因子得分。
第一步:数据预处理和分析
###标准化 scaler = StandardScaler().fit(data_9) #声明类,并用fit()方法计算后续标准化的mean与std print('\n均值:',scaler.mean_) #类属性:均值 print('方差:',scaler.var_) #类属性:方差 x_scaler = scaler.transform(data_9) #转换X print('\n标准化数据:\n',x_scaler)
第二步:因子分析——充分性检验
巴特利特P值小于0.01,KMO值大于0.6;说明此数据适合做因子分析。
## 充分性测试 ### p值小于0.01,kmo值大于0.6 from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity from factor_analyzer.factor_analyzer import calculate_kmo chi_val,p_val = calculate_bartlett_sphericity(x_scaler) kmo_all,kmo_val = calculate_kmo(x_scaler) print(p_val,kmo_val)
第三步:因子个数确定
特征值大于1的因子数有2个,且两个因子的累计方差有68%;因此确定因子个数为2个。
###因子个数确定 from factor_analyzer import FactorAnalyzer fa = FactorAnalyzer(x_scaler.shape[1],rotation=None) fa.fit(x_scaler) eigen_val,eigen_vector = fa.get_eigenvalues() var = fa.get_factor_variance print(eigen_val) print(eigen_vector) print(var)
第四步:做因子分析
调用因子分析函数,并得到因子载荷矩阵;
### 因子分析 fa = FactorAnalyzer(2,rotation='varimax') fa.fit(x_scaler) df_loading = pd.DataFrame(fa.loadings_,index=header_name[7:16]) df_loading
第五步:计算因子得分
### 计算因子得分 data_trans = pd.DataFrame(fa.transform(x_scaler)) plt.scatter(data_trans.loc[:,0],data_trans.loc[:,1]) plt.title("因子得分") plt.xlabel("factor1") plt.ylabel("factor2") plt.grid() plt.show()



