第04次作业-树
1.学习总结
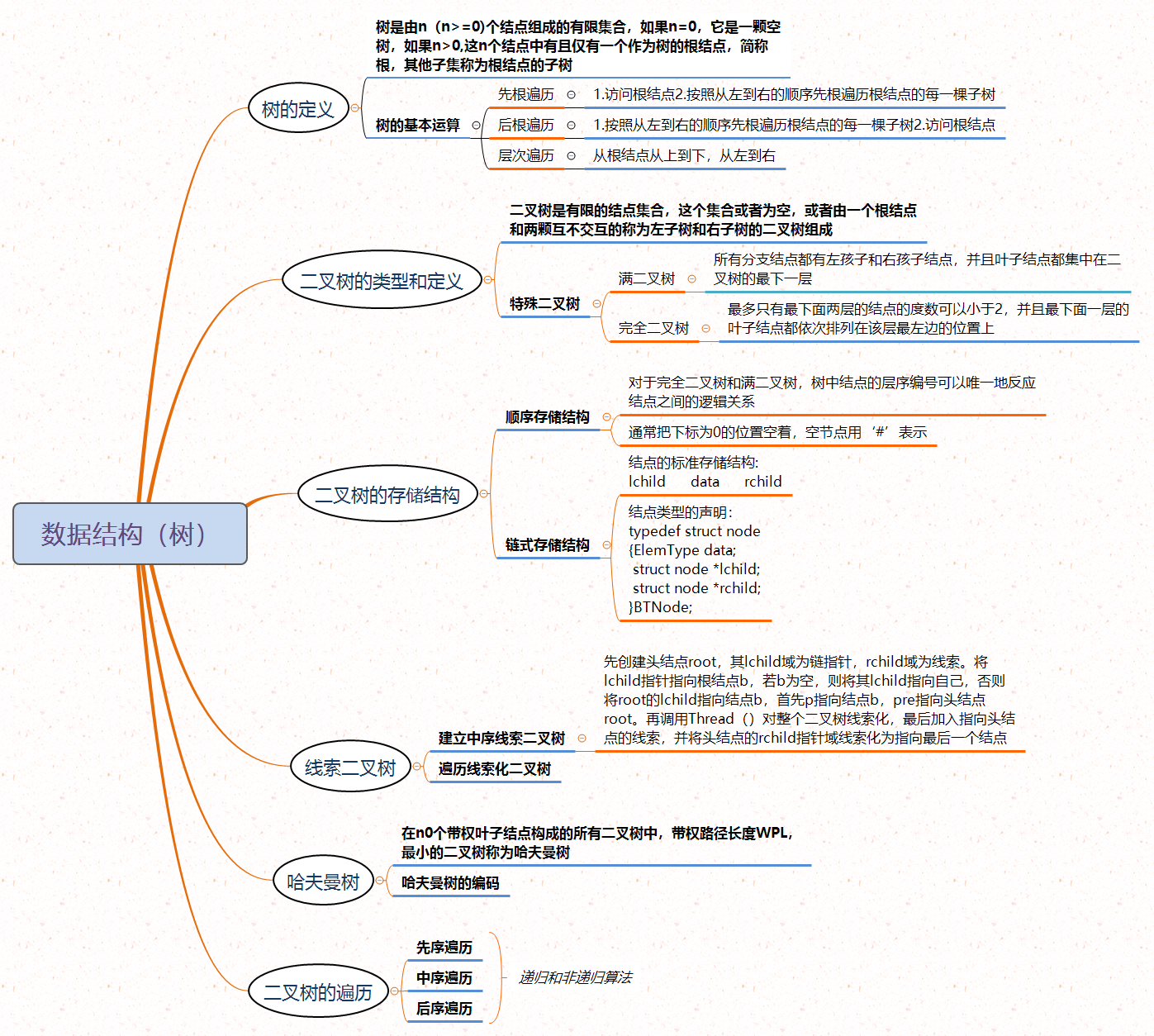
1.1树结构思维导图
1.2 树结构学习体会
困难:对树的遍历递归算法难以理解
解决的问题:对数据进行排序,还有查找和分类增加效率。
2.PTA实验作业
2.1 题目1:6-1 jmu-ds-二叉树操作集
2.2 设计思路(伪代码或流程图)
CreateBTree(&BT,str)
{ 新建结点->T;
新建队列->Q;
i=0;
if str为空
新建结点->BT;
BT->data=str[i];
BT->左,右=NULL;
BT进栈Q
end if
else 退出函数;
i++;
while Q不为空{
T=队列首个结点;
队首元素出队;
if str='#'或为空
T->左=NULL
end if
else {
新建T的左结点;
赋值=str[i];
T的左结点->左,右为空;
T的左结点进栈Q;
}
i++;
if str='#'或为空
T->右=NULL
end if
else {
新建T的右结点;
赋值=str[i];
T的右结点->左,右为空;
T的右结点进栈Q;
}
i++;
}
}
PreOrder(BT)
{定义静态变量flag=0;
if BT不为空
if flag为0 输出BT值
end if
else
输出‘ ’和BT值
flag=1;
PreOrder(BT->左);
PreOrder(BT->右);
end if
}
InOrder(BT)
{定义静态变量flag=0;
if BT不为空
InOrder(BT->左);
if flag为0 输出BT值
end if
else
输出‘ ’和BT值
flag=1;
InOrder(BT->右);
end if
}
PostOrder(BT)
{定义静态变量flag=0;
if BT不为空
PostOrder(BT->左);
PostOrder(BT->右);
if flag为0 输出BT值
end if
else
输出‘ ’和BT值
flag=1;
end if
}
2.1 题目2:6-4 jmu-ds-表达式树
2.2 设计思路(伪代码或流程图)
InitExpTree(&T,str)用两个栈建树
{新建栈s;
新建栈op;
‘#’入栈op;
i=0;
while(str不为空)
{
if 不是符号
新建结点T;
T赋值->str[i++];
T->左,右=NULL;
T进栈s;
end if;
else
{
switch 判断优先级
{
case‘<’;
str[i]进栈;
i++;
break;
case‘=’:
op出栈栈顶元素;
i++;
break;
case:‘>’:
新建T结点;
T赋值op栈顶元素;
T->右=s栈顶元素;
s栈顶元素出栈;
T->左=s栈顶元素;
s栈顶元素出栈;
T进栈s;
op栈顶元素出栈;
break;
}
}
}
while op不为‘#’
{新建T结点;
T赋值op栈顶元素;
T->右=s栈顶元素;
s出栈;
if s不为空
T->左=s栈顶元素;
s出栈;
end if;
}
}
}
2.3 代码截图



2.4 PTA提交列表说明

第一次没有把‘#’先入栈导致和题目的判断优先级子函数不匹配。修改了栈顶元素后就行了。
2.1 题目3:7-3 jmu-ds-二叉树层次遍历
2.2 设计思路(伪代码或流程图)
PrintAtlevel(T)层次遍历
{
static flag=0;
新建队列myqueue;
T进队myqueue;
while myqueue不为空
{
新建结点tmp为队顶元素;
if tmp->左不为空
tmp->左入队
end if
if tmp->右不为空
tmp->右入队
end if
if flag==0 cout<<tmp->data;end if
else cout<<空格<<tmp->data;
flag=1;
出队
}
2.3 代码截图
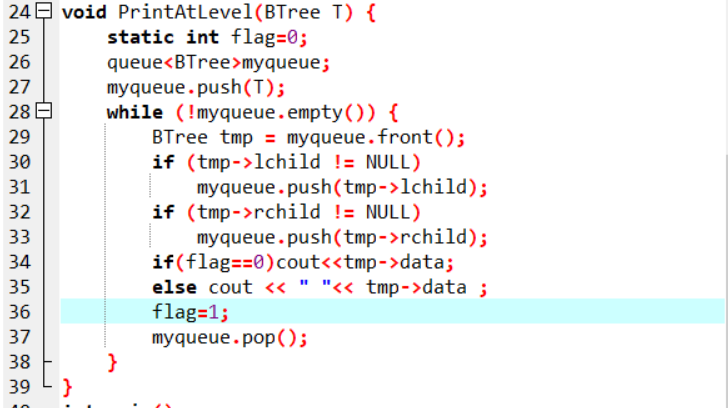
2.4 PTA提交列表说明

没什么大问题。
3.截图本周题目集的PTA最后排名

(3)PTA总分在180--230分:2分(必做题大部分做完)
4. 阅读代码(必做)
1.题目:平衡二叉树详解
具体代码如下:
1 #include <iostream> 2 #include <algorithm> 3 using namespace std; 4 #pragma once 5 6 //平衡二叉树结点 7 template <typename T> 8 struct AvlNode 9 { 10 T data; 11 int height; //结点所在高度 12 AvlNode<T> *left; 13 AvlNode<T> *right; 14 AvlNode<T>(const T theData) : data(theData), left(NULL), right(NULL), height(0){} 15 }; 16 17 //AvlTree 18 template <typename T> 19 class AvlTree 20 { 21 public: 22 AvlTree<T>(){} 23 ~AvlTree<T>(){} 24 AvlNode<T> *root; 25 //插入结点 26 void Insert(AvlNode<T> *&t, T x); 27 //删除结点 28 bool Delete(AvlNode<T> *&t, T x); 29 //查找是否存在给定值的结点 30 bool Contains(AvlNode<T> *t, const T x) const; 31 //中序遍历 32 void InorderTraversal(AvlNode<T> *t); 33 //前序遍历 34 void PreorderTraversal(AvlNode<T> *t); 35 //最小值结点 36 AvlNode<T> *FindMin(AvlNode<T> *t) const; 37 //最大值结点 38 AvlNode<T> *FindMax(AvlNode<T> *t) const; 39 private: 40 //求树的高度 41 int GetHeight(AvlNode<T> *t); 42 //单旋转 左 43 AvlNode<T> *LL(AvlNode<T> *t); 44 //单旋转 右 45 AvlNode<T> *RR(AvlNode<T> *t); 46 //双旋转 右左 47 AvlNode<T> *LR(AvlNode<T> *t); 48 //双旋转 左右 49 AvlNode<T> *RL(AvlNode<T> *t); 50 }; 51 52 template <typename T> 53 AvlNode<T> * AvlTree<T>::FindMax(AvlNode<T> *t) const 54 { 55 if (t == NULL) 56 return NULL; 57 if (t->right == NULL) 58 return t; 59 return FindMax(t->right); 60 } 61 62 template <typename T> 63 AvlNode<T> * AvlTree<T>::FindMin(AvlNode<T> *t) const 64 { 65 if (t == NULL) 66 return NULL; 67 if (t->left == NULL) 68 return t; 69 return FindMin(t->left); 70 } 71 72 73 template <typename T> 74 int AvlTree<T>::GetHeight(AvlNode<T> *t) 75 { 76 if (t == NULL) 77 return -1; 78 else 79 return t->height; 80 } 81 82 83 //单旋转 84 //左左插入导致的不平衡 85 template <typename T> 86 AvlNode<T> * AvlTree<T>::LL(AvlNode<T> *t) 87 { 88 AvlNode<T> *q = t->left; 89 t->left = q->right; 90 q->right = t; 91 t = q; 92 t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1; 93 q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1; 94 return q; 95 } 96 97 //单旋转 98 //右右插入导致的不平衡 99 template <typename T> 100 AvlNode<T> * AvlTree<T>::RR(AvlNode<T> *t) 101 { 102 AvlNode<T> *q = t->right; 103 t->right = q->left; 104 q->left = t; 105 t = q; 106 t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1; 107 q->height = max(GetHeight(q->left), GetHeight(q->right)) + 1; 108 return q; 109 } 110 111 //双旋转 112 //插入点位于t的左儿子的右子树 113 template <typename T> 114 AvlNode<T> * AvlTree<T>::LR(AvlNode<T> *t) 115 { 116 //双旋转可以通过两次单旋转实现 117 //对t的左结点进行RR旋转,再对根节点进行LL旋转 118 RR(t->left); 119 return LL(t); 120 } 121 122 //双旋转 123 //插入点位于t的右儿子的左子树 124 template <typename T> 125 AvlNode<T> * AvlTree<T>::RL(AvlNode<T> *t) 126 { 127 LL(t->right); 128 return RR(t); 129 } 130 131 132 template <typename T> 133 void AvlTree<T>::Insert(AvlNode<T> *&t, T x) 134 { 135 if (t == NULL) 136 t = new AvlNode<T>(x); 137 else if (x < t->data) 138 { 139 Insert(t->left, x); 140 //判断平衡情况 141 if (GetHeight(t->left) - GetHeight(t->right) > 1) 142 { 143 //分两种情况 左左或左右 144 145 if (x < t->left->data)//左左 146 t = LL(t); 147 else //左右 148 t = LR(t); 149 } 150 } 151 else if (x > t->data) 152 { 153 Insert(t->right, x); 154 if (GetHeight(t->right) - GetHeight(t->left) > 1) 155 { 156 if (x > t->right->data) 157 t = RR(t); 158 else 159 t = RL(t); 160 } 161 } 162 else 163 ;//数据重复 164 t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1; 165 } 166 167 template <typename T> 168 bool AvlTree<T>::Delete(AvlNode<T> *&t, T x) 169 { 170 //t为空 未找到要删除的结点 171 if (t == NULL) 172 return false; 173 //找到了要删除的结点 174 else if (t->data == x) 175 { 176 //左右子树都非空 177 if (t->left != NULL && t->right != NULL) 178 {//在高度更大的那个子树上进行删除操作 179 180 //左子树高度大,删除左子树中值最大的结点,将其赋给根结点 181 if (GetHeight(t->left) > GetHeight(t->right)) 182 { 183 t->data = FindMax(t->left)->data; 184 Delete(t->left, t->data); 185 } 186 else//右子树高度更大,删除右子树中值最小的结点,将其赋给根结点 187 { 188 t->data = FindMin(t->right)->data; 189 Delete(t->right, t->data); 190 } 191 } 192 else 193 {//左右子树有一个不为空,直接用需要删除的结点的子结点替换即可 194 AvlNode<T> *old = t; 195 t = t->left ? t->left: t->right;//t赋值为不空的子结点 196 delete old; 197 } 198 } 199 else if (x < t->data)//要删除的结点在左子树上 200 { 201 //递归删除左子树上的结点 202 Delete(t->left, x); 203 //判断是否仍然满足平衡条件 204 if (GetHeight(t->right) - GetHeight(t->left) > 1) 205 { 206 if (GetHeight(t->right->left) > GetHeight(t->right->right)) 207 { 208 //RL双旋转 209 t = RL(t); 210 } 211 else 212 {//RR单旋转 213 t = RR(t); 214 } 215 } 216 else//满足平衡条件 调整高度信息 217 { 218 t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1; 219 } 220 } 221 else//要删除的结点在右子树上 222 { 223 //递归删除右子树结点 224 Delete(t->right, x); 225 //判断平衡情况 226 if (GetHeight(t->left) - GetHeight(t->right) > 1) 227 { 228 if (GetHeight(t->left->right) > GetHeight(t->left->left)) 229 { 230 //LR双旋转 231 t = LR(t); 232 } 233 else 234 { 235 //LL单旋转 236 t = LL(t); 237 } 238 } 239 else//满足平衡性 调整高度 240 { 241 t->height = max(GetHeight(t->left), GetHeight(t->right)) + 1; 242 } 243 } 244 245 return true; 246 } 247 248 //查找结点 249 template <typename T> 250 bool AvlTree<T>::Contains(AvlNode<T> *t, const T x) const 251 { 252 if (t == NULL) 253 return false; 254 if (x < t->data) 255 return Contains(t->left, x); 256 else if (x > t->data) 257 return Contains(t->right, x); 258 else 259 return true; 260 } 261 262 //中序遍历 263 template <typename T> 264 void AvlTree<T>::InorderTraversal(AvlNode<T> *t) 265 { 266 if (t) 267 { 268 InorderTraversal(t->left); 269 cout << t->data << ' '; 270 InorderTraversal(t->right); 271 } 272 } 273 274 //前序遍历 275 template <typename T> 276 void AvlTree<T>::PreorderTraversal(AvlNode<T> *t) 277 { 278 if (t) 279 { 280 cout << t->data << ' '; 281 PreorderTraversal(t->left); 282 PreorderTraversal(t->right); 283 } 284 }
功能:平衡二叉树大部分操作和二叉查找树类似,主要不同在于插入删除的时候平衡二叉树的平衡可能被改变,并且只有从那些插入点到根结点的路径上的结点的平衡性可能被改变,因为只有这些结点的子树可能变化。
优点:很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。
地址:https://blog.csdn.net/u010442302/article/details/52713585
5. 代码Git提交记录截图



