c++基本数据结构
基本数据结构:
一.线性表
1.顺序结构
线性表可以用普通的一维数组存储。
你可以让线性表可以完成以下操作(代码实现很简单,这里不再赘述):
- 返回元素个数。
- 判断线性表是否为空。
- 得到位置为p的元素。
- 查找某个元素。
- 插入、删除某个元素:务必谨慎使用,因为它们涉及大量元素的移动。
2.链式结构
(1) 单链表:
1.定义:下面有一个空链表,表头叫head,并且表内没有任何元素。
struct node { int value; node *next; } arr[MAX]; int top=-1; node *head = NULL;
2.内存分配:在竞赛中不要用new,也不要用malloc、calloc——像下面一样做吧。
#define NEW(p) p=&arr[++top];p->value=0;p->next=NULL node *p; NEW(head); // 初始化表头 NEW(p); // 新建结点
3.插入:把q插入到p的后面。时间复杂度O(1)。
if (p!=NULL && q!=NULL) // 先判定是否为空指针。如果不是,继续。 { q->next=p->next; p->next=q; }
4.删除:把p的下一元素删除。时间复杂度O(1)。
if (p!=NULL && p->next!=NULL) // 先判定是否为空指针。如果不是,继续。 { node *q=p->next; p->next=q->next; // delete(q); // 如果使用动态内存分配,最好将它的空间释放。 }
5.查找或遍历:时间复杂度O(n)。
node *p=first; while (p!=NULL) { // 处理value // cout<<p->value<<'\t'; p=p->next; }
(2) 静态链表
指针的作用就是存储地址。如果我们找到了替代品,就可以放弃指针了。
需要把上面的定义改一下:
struct node { int value; int next; // 表示下一元素在arr中的下标 } arr[MAX];
(3) 循环链表
和单链表有一个重大区别:单链表最后一个元素的next指向NULL,而循环链表最后一个元素的next指向first。
遍历时要留心,不要让程序陷入死循环。
一个小技巧:如果维护一个表尾指针last,那么就可以在O(1)的时间内查找最后一个元素。同时可以防止遍历时陷入死循环。
(4) 双链表
1.定义:下面有一个空链表,表头叫first。
struct node { int value; node *next, *prev; } arr[MAX]; int top=-1; node *first = NULL; // 根据实际需要可以维护一个表尾指针last。
2.内存分配:最好不要使用new运算符或malloc、calloc函数。
#define NEW(p) p=arr+(++top);p->value=0;p->next=NULL;p->prev=NULL node *p; NEW(head); // 初始化表头 NEW(p); // 新建结点
3.插入:把q插入到p的后面。时间复杂度O(1)。
if (p==NULL||q==NULL) // 先判定是否为空指针。如果不是,继续。 { q->prev=p; q->next=p->next; q->next->prev=q; p->next=q; }
4.删除:把p的下一元素删除。时间复杂度O(1)。
if (p==NULL||p->next==NULL) // 先判定是否为空指针。如果不是,继续。 { node *q=p->next; p->next=q->next; q->next->prev=p; // delete(q); // 如果使用动态内存分配,最好将它的空间释放。 }
5.查找或遍历:从两个方向开始都是可以的。
(5) 将元素插入到有序链表中*
void insert(const node *head, node *p) { node *x, *y; y=head; do { x=y; y=x->next; } while ((y!=NULL) && (y->value < p->value); x->next=p; p->next=y; }
二.栈
(1) 栈的实现!
操作规则:先进后出,先出后进。
int stack[N], top=0; // top表示栈顶位置。
入栈:inline void push(int a) { stack[top++]=a; }
出栈:inline int pop() { return stack[--top];
栈空的条件:inline bool empty() { return top<0; }
如果两个栈有相反的需求,可以用这种方法节省空间:用一个数组表示两个栈。分别用top1、top2表示栈顶的位置,令top1从0开始,top2从N-1开始。
(2) DFS和栈
递归其实也用到了栈。每调用一次函数,都相当于入栈(当然这步操作“隐藏在幕后”)。函数调用完成,相当于出栈。
一般情况下,调用栈的空间大小为16MB。也就是说,如果递归次数太多,很容易因为栈溢出导致程序崩溃,即“爆栈”。
为了防止“爆栈”,可以将递归用栈显式实现。如果可行,也可以改成迭代、递推等方法。
使用栈模拟递归时,注意入栈的顺序——逆序入栈,后递归的要先入栈,先递归的要后入栈。
下面是非递归版本的DFS模板:
stack <int> s; // 存储状态 void DFS(int v, …) { s.push(v); // 初始状态入栈 while (!s.empty()) { int x = s.top(); s.pop(); // 获取状态 // 处理结点 if (x达到某种条件) { // 输出、解的数量加1、更新目前搜索到的最优值等 … return; } // 寻找下一状态。当然,不是所有的搜索都要这样寻找状态。 // 注意,这里寻找状态的顺序要与递归版本的顺序相反,即逆序入栈。 for (i=n-1;i>=0;i--) { s.push(… /*i对应的状态*/); } } // 无解 cout<<"No Solution."; }
三.队列
(1) 顺序队列
操作规则:先进先出,后进后出。
定义:int queue[N], front=0, rear=0;
front指向队列首个元素,rear指向队列尾部元素的右侧。
入队:inline void push(int a) { queue[rear++]=a; }
出队:inline int pop() { return queue[front++]; }
队空的条件:inline bool empty() { return front==rear; }
(2) 循环队列
循环队列——把链状的队列变成了一个环状队列。与上面的链状队列相比,可以节省很大空间。
定义:int queue[N], front=0, rear=0;
front指向队列首个元素,rear指向队列尾部元素的右侧。
入队:inline void push(int a) { queue[rear]=a; rear=(rear+1)%N; }
出队:inline int pop() { int t=queue[front]; front=(front+1)%N; return t; }
队满或队空的条件:inline bool empty() { return front==rear; }
队满和队空都符合上述条件。怎么把它们区分开呢?
第一种方法:令队列的大小是N+1,然后只使用N个元素。这样队满和队空的条件就不一样了。
第二种方法:在入队和出队同时记录队列元素个数。这样,直接检查元素个数就能知道队列是空还是满。
(3) BFS和队列
BFS要借助队列来完成,并且,将队列改成堆栈,BFS就变成了DFS。BFS的具体实现见42页“3.7 代码模板”。
四.二叉树
(1) 二叉树的链表存储法
struct node { int value; node *leftchild, *rightchild; //int id; // 结点编号。 //node *parent; // 指向父亲结点。 } arr[N]; int top=-1; node * head = NULL; #define NEW(p) p=&arr[++top]; p->leftchild=NULL; \ p->rightchild=NULL; p->value=0
(2) 完全二叉树的一维数组存储法
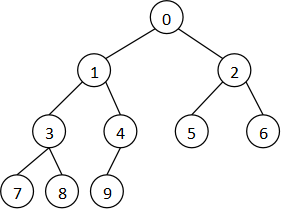
如果一个二叉树的结点严格按照从上到下、从左到右的顺序填充,就可以用一个一维数组保存。
下面假设这个树有n个结点,待操作的结点是r(0≤r<n)。
|
操作 |
宏定义 |
r的取值范围 |
|
r的父亲 |
#define parent(r) (((r)-1)/2) |
r≠0 |
|
r的左儿子 |
#define leftchild(r) ((r)*2+1) |
2r+1<n |
|
r的右儿子 |
#define rightchild(r) ((r)*2+2) |
2r+2<n |
|
r的左兄弟 |
#define leftsibling(r) ((r)-1) |
r为偶数且0<r≤n-1 |
|
r的右兄弟 |
#define rightsibling(r) ((r)+1) |
r为奇数且r+1<n |
|
判断r是否为叶子 |
#define isleaf(r) ((r)>=n/2) |
r<n |
(3) 二叉树的遍历
1. 前序遍历
void preorder(node *p) { if (p==NULL) return; // 处理结点p cout<<p->value<<' '; preorder(p->leftchild); preorder(p->rightchild); }
2. 中序遍历
void inorder(node *p) { if (p==NULL) return; inorder(p->leftchild); // 处理结点p cout<<p->value<<' '; inorder(p->rightchild); }
3. 后序遍历
void postorder(node *p) { if (p==NULL) return; postorder(p->leftchild); postorder(p->rightchild); // 处理结点p cout<<p->value<<' '; }
假如二叉树是通过动态内存分配建立起来的,在释放内存空间时应该使用后序遍历。
4. 宽度优先遍历(BFS)
首先访问根结点,然后逐个访问第一层的结点,接下来逐个访问第二层的结点……
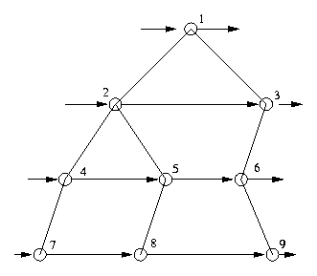
node *q[N]; void BFS(node *p) { if (p==NULL) return; int front=1,rear=2; q[1]=p; while (front<rear) { node *t = q[front++]; // 处理结点t cout<<t->value<<' '; if (t->leftchild!=NULL) q[rear++]=t->leftchild; if (t->rightchild!=NULL) q[rear++]=t->rightchild; } }
对于完全二叉树,可以直接遍历:
for (int i=0; i<n; i++) cout<<a[i]<<' ';
(4) 二叉树重建
【问题描述】二叉树的遍历方式有三种:前序遍历、中序遍历和后序遍历。现在给出其中两种遍历的结果,请输出第三种遍历的结果。
【分析】
前序遍历的第一个元素是根,后序遍历的最后一个元素也是根。所以处理时需要到中序遍历中找根,然后递归求出树。
注意!输出之前须保证字符串的最后一个字符是'\0'。
1. 中序+后序→前序
void preorder(int n, char *pre, char *in, char *post) { if (n<=0) return; int p=strchr(in, post[n-1])-in; pre[0]=post[n-1]; preorder(p, pre+1, in, post); preorder(n-p-1, pre+p+1, in+p+1, post+p); }
2. 前序+中序→后序
void postorder(int n, char *pre, char *in, char *post) { if (n<=0) return; int p=strchr(in, pre[0])-in; postorder(p, pre+1, in, post); postorder(n-p-1, pre+p+1, in+p+1, post+p); post[n-1]=pre[0]; }
3. 前序+后序→中序
“中+前”和“中+后”都能产生唯一解,但是“前+后”有多组解。下面输出其中一种。
bool check(int n, char *pre, char *post) // 判断pre、post是否属于同一棵二叉树 { bool b; for (int i=0; i<n; i++) { b=false; for (int j=0; j<n; j++) if (pre[i]==post[j]) { b=true; break; } if (!b) return false; } return true; } void inorder(int n, char *pre, char *in, char *post) { if (n<=0) return; int p=1; while (check(p, pre+1, post)==false && p<n) p++; if (p>=n) p=n-1; // 此时,如果再往inorder里传p,pre已经不含有效字符了。 inorder(p, pre+1, in, post); in[p]=pre[0]; inorder(n-p-1, pre+p+1, in+p+1, post+p); }
(5) 求二叉树的直径*
从任意一点出发,搜索距离它最远的点,则这个最远点必定在树的直径上。再搜索这个最远点的最远点,这两个最远点的距离即为二叉树的直径。
求树、图(连通图)的直径的思想是相同的。
// 结点编号从1开始,共n个结点。 struct node { int v; node *parent, *leftchild, *rightchild; } a[1001], *p; int maxd; bool T[1003]; #define t(x) T[((x)==NULL)?0:((x)-a+1)] node *p; void DFS(node * x, int l) { if (l>maxd) maxd=l, p=x; if (x==NULL) return; t(x)=false; if (t(x->parent)) DFS(x->parent, l+1); if (t(x->leftchild)) DFS(x->leftchild, l+1); if (t(x->rightchild)) DFS(x->rightchild, l+1); } int distance(node *tree) // tree已经事先读好 { maxd=0; memset(T, 0, sizeof(T)); for (int i=1; i<=n; i++) T[i]=true; DFS(tree,0); maxd=0; memset(T, 0, sizeof(T)); for (int i=1; i<=n; i++) T[i]=true; DFS(p,0); return maxd; }
五.并查集
并查集最擅长做的事情——将两个元素合并到同一集合、判断两个元素是否在同一集合中。
并查集用到了树的父结点表示法。在并查集中,每个元素都保存自己的父亲结点的编号,如果自己就是根结点,那么父亲结点就是自己。这样就可以用树形结构把在同一集合的点连接到一起了。
并查集的实现:
struct node { int parent; // 表示父亲结点。当编号i==parent时为根结点。 int count; // 当且仅当为根结点时有意义:表示自己及子树元素的个数 int value; // 结点的值 } set[N]; int Find(int x) // 查找算法的递归版本(建议不用这个) { return (set[x].parent==x) ? x : (set[x].parent = Find(set[x].parent)); } int Find(int x) // 查找算法的非递归版本 { int y=x; while (set[y].parent != y) // 寻找父亲结点 y = set[y].parent; while (x!=y) // 路径压缩,即把途中经过的结点的父亲全部改成y。 { int temp = set[x].parent; set[x].parent = y; x = temp; } return y; } void Union(int x, int y) // 小写的union是关键字。 { x=Find(x); y=Find(y); // 寻找各自的根结点 if (x==y) return; // 如果不在同一个集合,合并 if (set[x].count > set[y].count) // 启发式合并,使树的高度尽量小一些 { set[y].parent = x; set[x].count += set[y].count; } else { set[x].parent = y; set[y].count += set[x].count; } } void Init(int cnt) // 初始化并查集,cnt是元素个数 { for (int i=1; i<=cnt; i++) { set[i].parent=i; set[i].count=1; set[i].value=0; } } void compress(int cnt) // 合并结束,再进行一次路径压缩 { for (int i=1; i<=cnt; i++) Find(i); }
说明:
使用之前调用Init()!
Union(x,y):把x和y进行启发式合并,即让节点数比较多的那棵树作为“树根”,以降低层次。
Find(x):寻找x所在树的根结点。Find的时候,顺便进行了路径压缩。
上面的Find有两个版本,一个是递归的,另一个是非递归的。
判断x和y是否在同一集合:if (Find(x)==Find(y)) ……
在所有的合并操作结束后,应该执行compress()。
并查集的效率很高,执行m次查找的时间约为O(5m)。
六.总结
数据结构是计算机科学的重要分支。选择合适的数据结构,可以简化问题,减少时间的浪费。
1. 线性表
线性表有两种存储方式,一种是顺序存储,另一种是链式存储。前者只需用一维数组实现,而后者既可以用数组实现,又可以用指针实现。
顺序表的特点是占用空间较小,查找和定位的速度很快,但是插入和删除元素的速度很慢(在尾部速度快);链表和顺序表正好相反,它的元素插入和删除速度很快,但是查找和定位的速度很慢(同样,在首尾速度快)。
2. 栈和队列
栈和队列以线性表为基础。它们的共同点是添加、删除元素都有固定顺序,不同点是删除元素的顺序。队列从表头删除元素,而栈从表尾删除元素,所以说队列是先进先出表,堆栈是先进后出表。
栈和队列在搜索中有非常重要的应用。栈可以用来模拟深度优先搜索,而广度优先搜索必须用队列实现。
有时为了节省空间,栈的两头都会被利用,而队列会被改造成循环队列。
3. 二叉树
上面几种数据结构都是线性结构。而二叉树是一种很有用的非线性结构。二叉树可以采用以下的递归定义:二叉树要么为空,要么由根结点、左子树和右子树组成。左子树和右子树分别是一棵二叉树。
计算机中的树和现实生活不同——计算机里的树是倒置的,根在上,叶子在下。
完全二叉树:一个完全二叉树的结点是从上到下、从左到右地填充的。如果高度为h,那么0~h-1层一定已经填满,而第h层一定是从左到右连续填充的。
通常情况下,二叉树用指针实现。对于完全二叉树,可以用一维数组实现(事先从0开始编号)。
访问二叉树的所有结点的过程叫做二叉树的遍历。常用的遍历方式有前序遍历、中序遍历、后序遍历,它们都是递归完成的。
4. 树
树也可以采用递归定义:树要么为空,要么由根结点和n(n≥0)棵子树组成。
森林由m(m≥0)棵树组成。
二叉树不是树的一种,因为二叉树的子树中有严格的左右之分,而树没有。这样,树可以用父结点表示法来表示(当然,森林也可以)。并查集的合并、查询速度很快,它就是用父结点表示法实现的。
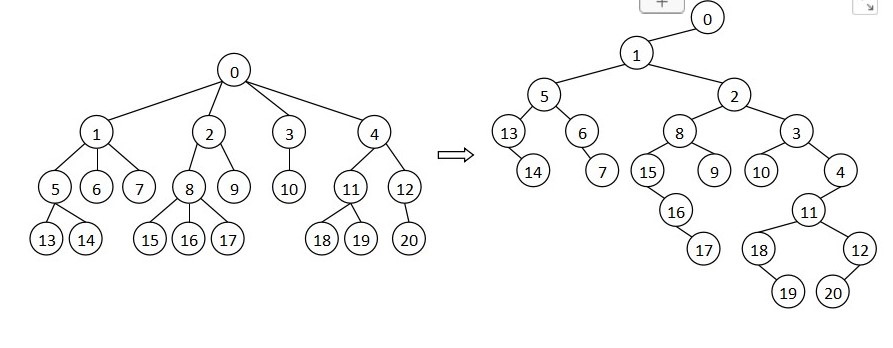
不过父结点表示法的遍历比较困难,所以常用“左儿子右兄弟”表示法把树转化成二叉树。
树的遍历和二叉树的遍历类似,不过不用中序遍历。它们都是递归结构,所以可以在上面实施动态规划。
树作为一种特殊的图,在图论中也有广泛应用。
树的表示方法有很多种。
第一种是父节点表示法,它适合并查算法,但不便遍历。
第二种是子节点表表示法。
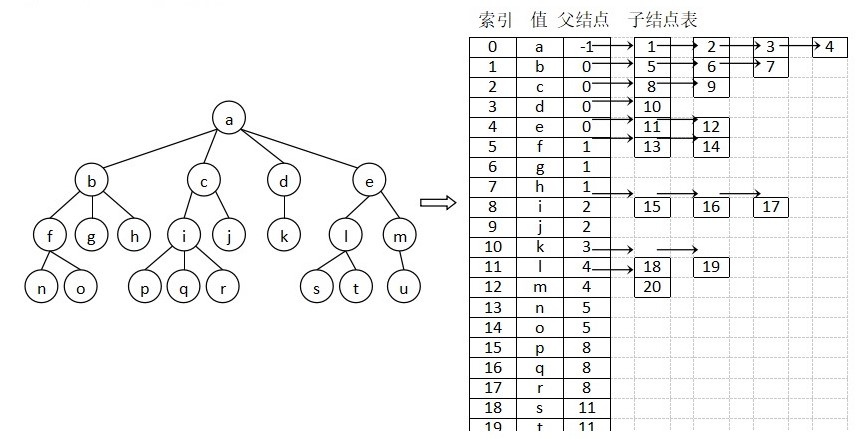
第三种是“左儿子右兄弟”表示法。
本文来自博客园,作者:张其勋,转载请注明原文链接:https://www.cnblogs.com/zhangqixun/p/17301711.html


