回溯算法————n皇后、素数串
回溯就是算法是搜索算法中一种控制策略,是一个逐个试探的过程。在试探的过程中,如果遇到错误的选择,就会回到上一步继续选择下一种走法,一步一步的进行直到找到解或者证明无解为止。
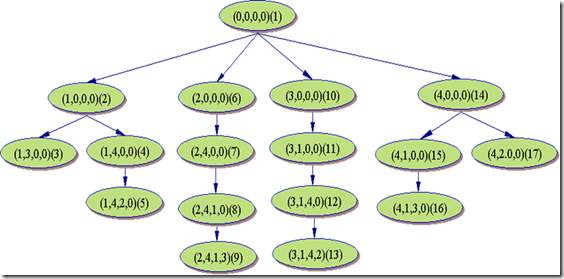
如下是一个经典回溯问题n皇后的解答树:
下面就从n皇后说起:
【问题描述】
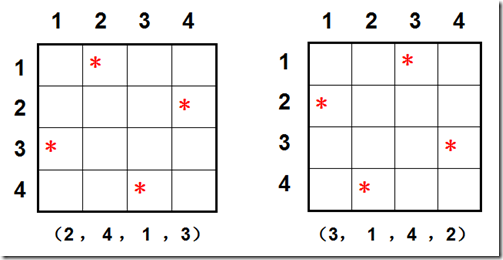
在n×n的国际象棋盘上,放置n个皇后,使任何一个皇后都不能吃掉另一个,需满足的条件是:同一行、同一列、同一对角线上只能有一个皇后。求所有满足要求的放置方案。4皇后的放置方案如下:
【输入】一个正整数n。
【输出】每行代表一种放置方案:第i行的第一个数是i,表示第i种方案,后面一个冒号,然后是用空格隔开的n个数,其中第i个数x[i]表示第i行上的皇后放在第x[i]列;最后一行:一个整数,表示方案总数。
【样例输入】
4
【样例输出】
1:2 4 1 3
2:3 1 4 2
2
这个题目简直是太经典了,一提到回溯第一个想到的就是它。这个题非常的通俗易懂,就是在一个n*n的棋盘上满足条件地放置n个皇后,每种组合搜一遍就好了。在搜的过程中判断下一步的某种方向是否可以走,如果可以的话就进入下一层,如果不符合要求就搜下一个方向,搜完这一层的所有方向以后就回到上一层,继续搜上一层的下一个方向。
不知道大家看懂了没有,如果没看懂,看代码就懂了。。
上代码:
#include<iostream>
#include<cstdio>
using namespace std;
int n;
int sum=0;//解法存放个数
int a[100000];//存放皇后位置数据
bool b[1000000]={0},c[1000000]={0},d[10000000]={0};//b存储y方向,c、d存储对角线
void print()
{
sum++;
cout<<sum<<':';
for(int i=1;i<=n;i++)
{
cout<<a[i]<<' ';
}
cout<<endl;
}
int search(int x)
{
for(int j=1;j<=n;j++)//遍历本层中每种方向
{
if((!b[j])&&(!c[x+j])&&(!d[x-j+n-1]))//如果满足条件
{
a[x]=j;//存入皇后数据
b[j]=1;//占领y轴
c[x+j]=1;//占领对角线
d[x-j+n-1]=1;//占领对角线
if(x==n)
{
print();//如果有完整解,输出
}
else
{
search(x+1);//如果没有继续找下一行
}
b[j]=0;//找完之后取消占领
c[x+j]=0;
d[x-j+n-1]=0;
}
}
}
int main()
{
cin>>n;
search(1);//从第一个开始找
cout<<sum;
}
把思想带到代码里应该就看懂了吧。
回溯就是这样一层一层的找,找完本层返回上一层继续找,直到找到正确解为止。
继续再看一道题:
3、素数链
设计程序将1。。。n排成一排,使任意两个相邻的数的和为素数。第1个和最后一个的和也为素数.输出一种方案即可。
输入:
n (n<=100)
输出:
1到n的一个序列,中间用一个空格隔开。第一个数为1。
如果无解输出-1。
样例输入:
10
样例输出:
1 2 3 4 7 6 5 8 9 10
这道题和刚才那道n皇后的思路是一样的,遍历所有可能,在遍历的过程中判断,如果可以就继续搜下一层。
代码如下:
#include<cstdio>
#include<iostream>
const int maxx=1000;
using namespace std;
int n;
int numguo[maxx]={0};
bool guo[maxx]={0},pguo=0;
int c=0;
int sushu(int x)//验证素数的函数
{
//关于判断素数的题很早就做过,这里我就不解释了
int i=2;
while(i<x)
{
if(x%i==0)
return 0;//如果不是直接跳出返回0
i++;
}
return 1;//如果是的话返回1
}
int panduan()
{
int t;
for(int i=1;i<n;i++)//判断是否达到要求
{
if(!sushu(numguo[i]+numguo[i+1]))//这里我直接放到函数里去验证
{
return 0;//如果不是素数就直接跳出返回0
}
}
if(!sushu(numguo[n]+numguo[1])) return 0;//注意别忘了最后一个和第一个数字的和是否为素数
return 1;//正确的话返回1
}
int print()
{
c++;//可能方法+1
for(int i=1;i<=n;i++){
cout<<numguo[i]<<' ';
}
cout<<endl;
}
int search(int x)
{
for(int i=1;i<=n;i++)//搜索本层中每种可能
{
if(!guo[i])
{
guo[i]=1;//占领
numguo[x]=i;//标记
if(x==n)//如果达到数量要求
{
if(panduan())//如果符合要求
{
if(!pguo)//如果没输出过
{
pguo=1;//输出过
print();//输出
return 0;//搜到就直接跳出
}
}
}
else search(x+1);
guo[i]=0;
numguo[x]=0;
}
}
}
int main()
{
cin>>n;
search(1);//从第一个开始找
if(!c) cout<<"-1";//如果没可能就输出“-1”
return 0;
}
这些代码中我用了很多的函数,这样节约了代码长度,也更加方便(个人觉得)。
回溯就是这个中心思想,一步步往下搜,一层层的搜,直到搜完或找到结果为止。
其实上面两道题都是很水的基础,再往后还有回溯遍历图、树等等等等。。
ending。。。