基数、希尔、计数、桶排序

一、基数排序

import random
from timewrap import *

def list_to_buckets(li, iteration):#这个是用来比较每个位置的大小的数字

    """
    因为分成10个本来就是有序的所以排出来就是有序的。
    :param li: 列表
    :param iteration: 装桶是第几次迭代
    :return:
    """
    buckets = [[] for _ in range(10)]
    print('buckests',buckets)
    for num in li:
        digit = (num // (10 ** iteration)) % 10
        buckets[digit].append(num)
    print(buckets)
    return buckets

def buckets_to_list(buckets):#这个是用来出数的
    return [num for bucket in buckets for num in bucket]
    # li = []
    # for bucket in buckets:
    #     for num in bucket:
    #         li.append(num)

@cal_time
def radix_sort(li):
    maxval = max(li) # 10000
    it = 0
    while 10 ** it <= maxval:#这个是循环用来，在以前一次排序的基础上在排序。
        li = buckets_to_list(list_to_buckets(li, it))
        it += 1
    return li

# li = [random.randint(0,1000) for _ in range(100000)]
li = [random.randint(0,10) for _ in range(10)]
li=[5555,5525,9939,9999,6,3,8,9]
s=radix_sort(li)
print(s)

 

二、希尔排序

思路：

• 希尔排序是一种分组插入排序算法。
• 首先取一个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1，在各组内进行直接插入排序；
• 取第二个整数d2=d1/2，重复上述分组排序过程，直到di=1，即所有元素在同一组
• 希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序。

代码实现、

def insert_sort(li):#插入排序
    for i in range(1, len(li)):
        # i 表示无序区第一个数
        tmp = li[i] # 摸到的牌
        j = i - 1 # j 指向有序区最后位置
        while li[j] > tmp and j >= 0:
            #循环终止条件： 1. li[j] <= tmp; 2. j == -1
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp

def shell_sort(li):#希尔排序  与插入排序区别就是把1变成d
    d = len(li) // 2
    while d > 0:
        for i in range(d, len(li)):
            tmp = li[i]
            j = i - d
            while li[j] > tmp and j >= 0:
                li[j+d] = li[j]
                j -= d
            li[j+d] = tmp
        d = d >> 1




li=[5,2,1,4,5,69,20,11]
shell_sort(li)
print(li)

 

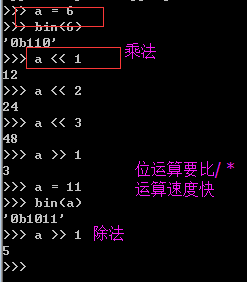
希尔排序的复杂度特别复杂，取决于d，分组的长度二、位移运算符

三、计数排序：

统计每个数字出现了几次

#计数排序
# 0 0 1 1 2 4 3 3 1 4 5 5
import random
import copy
from timewrap import *

@cal_time
def count_sort(li, max_num = 100):
    count = [0 for i in range(max_num+1)]
    for num in li:
        count[num]+=1
    li.clear()
    for i, val in enumerate(count):
        for _ in range(val):
            li.append(i)

@cal_time
def sys_sort(li):
    li.sort()

li = [random.randint(0,100) for i in range(100000)]
li1 = copy.deepcopy(li)
count_sort(li)
sys_sort(li1)

 计数排序这么快，为什么不用计数排序呢？因为他是有限制的，你要知道列表中的最大数

如果一下来了一个很大的数，比如10000，那么占的空间就的这么大，

计数排序占用的空间和列表的范围有关系

解决这种问题的方法，可以用桶排序，都放进去可以在进行其他的排序。比如插入排序。

四、桶排序

    在计数排序中，如果元素的范围比较大(比如在1到1亿之间)，如何改造算法？

     桶排序，首先将将元素分在不同的桶中，在对每个桶中的元素排序。

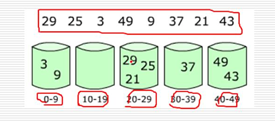
多关键字排序

先对十位进行排序，再根据 十位进行排序

要用两个函数，一个用来装桶，一个用来出桶

默认10个桶，找到个位，十位，分别放在对应的桶里的位置

 

     桶排序的表现取决于数据的分布。也就是需要对不同数据排序时采取不同的分桶策略。

     平均情况时间复杂度：O(n+k)

     最坏情况时间复杂度：O(n+k)

     空间复杂度：O(nk)

    先分成若干个桶，桶内用插入排序。

 

例子

1：给两个字符串S和T，判断T是否为S的重新排列后组成的单词：

  s="anagram",t="nagaram",return true

   s='cat',t='car',return false

代码如下：

s = "anagram"
t = "nagaram"

def ss(s,t):
    return  sorted(list(s))==sorted(list(t))
y=ss(s,t)
print(y)

2、‘’

二维的坐标变成一维的坐标

X*b +y =i

(x,y) ->i

 

i//n----》x

i%n---->n

 

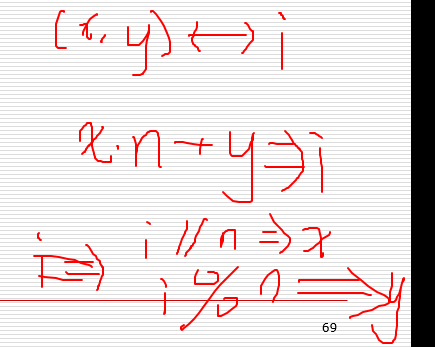
def searchMatrix(matrix, target):
    m = len(matrix)
    # print('m', m)
    if m == 0:
        return False
    n = len(matrix[0])
    if n == 0:
        return False
    low = 0
    high = m * n - 1
    # print('high',high)
    while low <= high:
        mid = (low + high) // 2
        x, y = divmod(mid, n)
        if matrix[x][y] > target:
            high = mid - 1
        elif matrix[x][y] < target:
            low = mid + 1
        else:
            return True
    else:
        return False


s = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
]
# print(searchMatrix(s, 1))
# print(searchMatrix(s, 2))
# print(searchMatrix(s, 3))
# print(searchMatrix(s, 4))
# print(searchMatrix(s, 5))
# print(searchMatrix(s, 6))
print(searchMatrix(s, 7))
# print(searchMatrix(s, 8))
# print(searchMatrix(s, 9))

 3.给定一个列表和一个整数，设计算法找两个数的小标，使得两个数之和为给定的整数。保证肯定仅有一个结果。

     例如：列表[1,2,5,4]与目标整数3，1+2=3，结果为(0,1)

方式一：

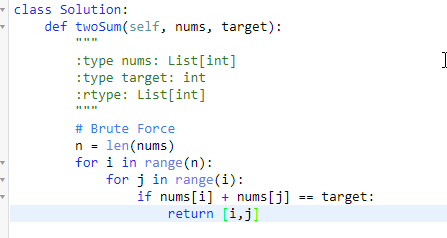
方式二：

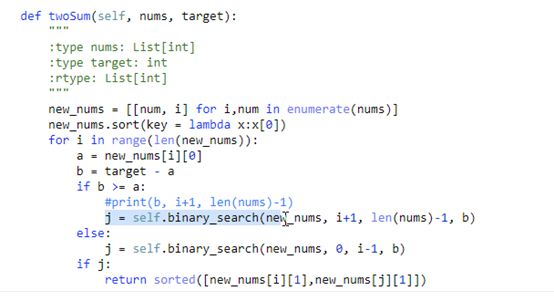
方式三

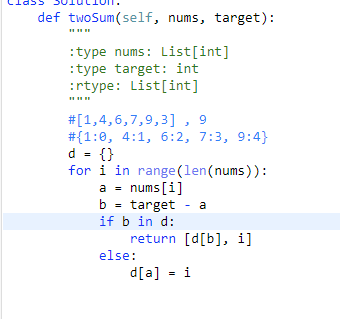
方式四和三一样

def twoSum(num, target):
    dict = {}
    for i in range(len(num)):
        print(dict)
        x = num[i]
        if target - x in dict:
            return dict[target - x], i
        dict[x] = i



l = [1, 2, 5, 4]
print(twoSum(l, 7))