几个简单DP(递推)集合
HDU 2044
一只小蜜蜂...
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 75858 Accepted Submission(s):
27227
Problem Description
有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房,不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
其中,蜂房的结构如下所示。
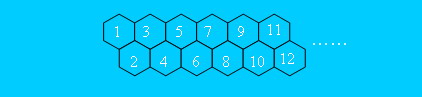
其中,蜂房的结构如下所示。

Input
输入数据的第一行是一个整数N,表示测试实例的个数,然后是N
行数据,每行包含两个整数a和b(0<a<b<50)。
Output
对于每个测试实例,请输出蜜蜂从蜂房a爬到蜂房b的可能路线数,每个实例的输出占一行。
Sample Input
2
1 2
3 6
Sample Output
1
3

1 #include <iostream> 2 #include <bits/stdc++.h> 3 using namespace std; 4 const int maxn = 55; 5 typedef long long ll; 6 ll dp[maxn]; 7 void pre() { 8 dp[1] = 1; 9 dp[2] = 2; 10 11 for(int i = 3; i < maxn; i++) { 12 dp[i] = dp[i-1]+dp[i-2]; 13 } 14 } 15 int main() 16 { 17 pre(); 18 int t; 19 cin>>t; 20 while(t--) { 21 int a,b; 22 cin>>a>>b; 23 printf("%lld\n",dp[b-a]); 24 } 25 return 0; 26 }
HDU 2050
折线分割平面
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 30984 Accepted Submission(s):
20934
Problem Description
我们看到过很多直线分割平面的题目,今天的这个题目稍微有些变化,我们要求的是n条折线分割平面的最大数目。比如,一条折线可以将平面分成两部分,两条折线最多可以将平面分成7部分,具体如下所示。


Input
输入数据的第一行是一个整数C,表示测试实例的个数,然后是C
行数据,每行包含一个整数n(0<n<=10000),表示折线的数量。
Output
对于每个测试实例,请输出平面的最大分割数,每个实例的输出占一行。
Sample Input
2
1
2
Sample Output
2
7
和今年的湘潭热身赛一个题很想的,我的推导就是当前图形和前一个的图形的关系是:一条线下去可以相交的最大交点数的倍数+一个常数
推一下当前分割数 d(n) = d(n-1) + 2*t + 1; t为一条线段交点数
t和n的关系是:t = 2*(n-1);
合并就出来了:
#include <iostream> #include <bits/stdc++.h> using namespace std; const int maxn = 10000+10; typedef long long ll; ll dp[maxn]; void pre() { dp[1] = 2; for(int i = 2; i < maxn; i++) { dp[i] = dp[i-1] + 4*i - 3; } } int main() { pre(); int t; cin>>t; while(t--) { int a; cin>>a; printf("%lld\n",dp[a]); } return 0; }



