一道图的题

最近遇到的一道算法题：
有一个坐标系，输入一组数据input:, eg:

const input = [
    [0, 0],
    [1, 1],
    [3, 1],
    [1, 2],
    [3, 2],
    [2, 3],
    [1, 4],
    [2, 4],
    [4, 4],
    [4, 5],
    [3, 4]
];

input的每个值(数组)是一组坐标，对应到图是这样的，

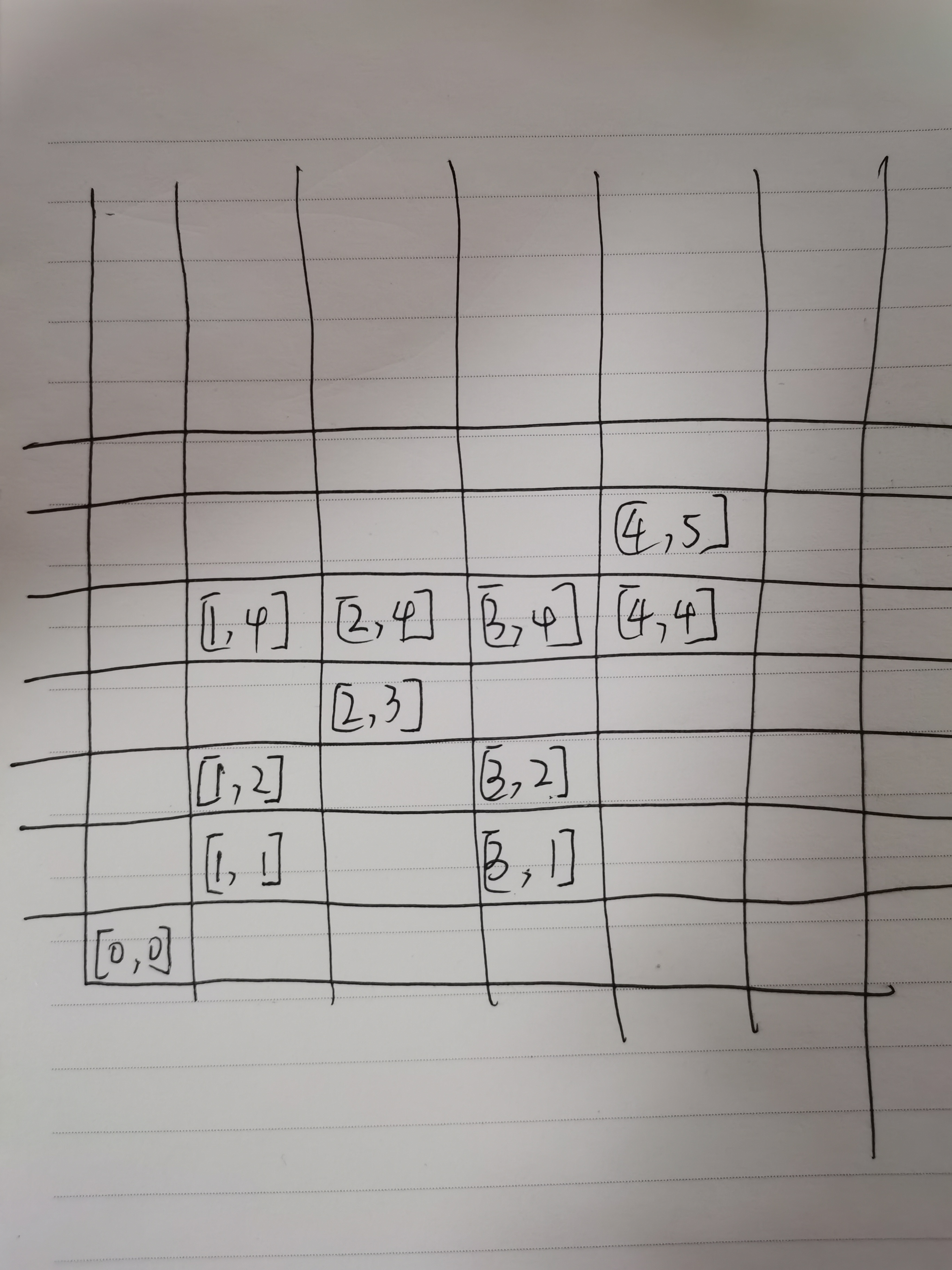
输出为：

output:
[
  [[0, 0]],
  [[1,1], [1,2]],
  [[3,1], [3,2]],
  [[1,4], [2,4], [2,3], [3,4], [4,4], [4,5]]
]

即要求相邻的坐标为一组，输出符合这种要求的所有的组。

一开始只看数据以为是模拟找数字相同的，后面对照着图看确定是一个图的题，这不就是以前大学图论里的求所有的连通分量嘛。。。还好以前大学搞过一段时间图论，有点基础和概念底子，不知道的一般前端现场看到这种题可能比较懵吧。。。

我的思路就是建立坐标系，把input的输入变为坐标系的1，其余0或者undefined，从input的每个坐标开始dfs，如果没搜过push进当前的group，然后朝四个方向继续dfs。这里有个细节就是注意要标志下是否搜索过，我当时使用map存了一下，如果push进过group，就存进map里，dfs进入的时候统一判断。后面下来想了下其实直接push完把当前坐标系的值重置为0就好了。下面是我当时通过样例的代码，当时还要求现场bug free，又费了会儿时间，感觉这种大题有思路还要现场bug free还是费点时间的。如果这道题如果只是在意考察思路，可以变成求连通分量的数量，少处理点坐标系相关的可以节省时间。

function solve(input) {
    let mpMax = 6;
    let ans = [];
    let mp = [];
    for (let i = 0; i < mpMax; i++) {
        mp[i] = [];
        for (let j = 0; j < mpMax; j++) {
            mp[i][j] = 0;
        }
    }
    input.forEach((item) => {
        mp[item[0]][item[1]] = 1;
    });
    let map = new Map();
    for (let k = 0; k < input.length; k++) {
        let item = input[k];
        let i = item[0];
        let j = item[1];
        if (map.has(i.toString() + j.toString())) continue;
        let ret = [];
        // ret.push(item);
        dfs(i, j, ret);
        ans.push(ret);
    }
    return ans;
    function dfs(i, j, ret) {
        // 边界条件
        if (i < 0 || i > mpMax || j < 0 || j > mpMax || mp[i][j] !== 1) {
            return;
        }
        if (map.has(i.toString() + j.toString())) return;
        console.log('mp[i][j]', i, j, mp[i][j]);
        if (mp[i][j]) {
            // ret.push(mp[i][j]);
            ret.push([i, j]);
            map.set(i.toString() + j.toString(), 1);
        }
        dfs(i, j + 1, ret);
        dfs(i, j - 1, ret);
        dfs(i + 1, j, ret);
        dfs(i - 1, j, ret);
    }
}