HDU1165： Eddy's research II（递推）

题目：http://acm.hdu.edu.cn/showproblem.php?pid=1165

果断不擅长找规律啊，做这种题静不下心来。

Ackermann function can be defined recursively as follows: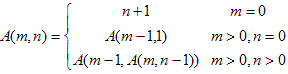

递推如上图，

0<m<=3,0<=n<=1000000,,当m==3时，n>=0&&n<=24.

首先发现a(0,i)=i+1;

另外n==0时，a(1,0)=a(0,1)=2;

当m==1,n>0时，a(1,n)=a(0,a(1,n-1)=a(1,n-1)+1;

有上式找到当m==1时的递推公式，a(1,i)=a(1,i-1)+1;(其中a(1,0)=2);

所以a(1,i)=i+2;

同理，当m==2，n>0时，a(2,n)=a(1,a(2,n-1))=a(2,n-1)+2;(其中a(2,0)=a(1,1)=3)

所以a(2,i)=2*i+3;

所以a(3,i)=a(2,a(3,i-1))=2*a(3,i-1))+3;

由此可以解出结果。

代码如下：

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#define inf 0x3f3f3f3f
using namespace std;
int dp[4][1000010],n,m;
int main()
{
    for(int i=0;i<=1000000;i++)
        dp[0][i]=i+1;
    dp[1][0]=2;
    for(int i=1;i<=1000000;i++)
        dp[1][i]=i+2;
     dp[2][0]=3;
    for(int i=1;i<=1000000;i++)
    {
        dp[2][i]=dp[2][i-1]+2;//2*i+3
    }
    dp[3][0]=5;
    for(int i=1;i<=24;i++)
    {
        dp[3][i]=2*(dp[3][i-1])+3;
    }
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        printf("%d\n",dp[n][m]);
    }
    return 0;
}