POJ2513:Colored Sticks(字典树+欧拉路径+并查集)
http://poj.org/problem?id=2513
Description
Input
Output
Sample Input
blue red red violet cyan blue blue magenta magenta cyan
Sample Output
Possible
Hint
大致题意:
给定一些木棒,木棒两端都涂上颜色,求是否能将木棒首尾相接,连成一条直线,要求不同木棒相接的一边必须是相同颜色的。
由图论知识可以知道,无向图存在欧拉路的充要条件为:
① 图是连通的;
② 所有节点的度为偶数,或者有且只有两个度为奇数的节点。
分析:欧拉路径问题,求是否有欧拉通路(欧拉回路的概念)
1.定理:无向图G有欧拉通路的充分必要条件是G为连通图,并且G仅有两个奇度结点或者无奇度结点。
(1)当G是仅有两个奇度结点的连通图时,G的欧拉通路必以此两个结点为端点。
(2)当G是无奇度结点的连通图时,G必有欧拉回路。
2.一个有向图D具有欧拉通路,当且仅当D是连通的,且除了两个顶点外,其余顶点的入度均等于出度,这两个特殊的顶点中,一个顶点的入度比出度大1,另一个顶点的入度比出度小1. 推论:一个有向图D是欧拉图(具有欧拉回路),当且仅当D是连通的,且所有顶点的出度等于入度。
3.trie树是一种存储名称的普遍方法。
解法:并查集判断是否连通,用trie存储每种颜色。看度是否符合要求。
#include <iostream> #include <string.h> #include <stdio.h> #include <stdlib.h> #define N 500002 using namespace std; typedef struct node { int flag; struct node *next[26]; }*Tree,Node; char a[10],b[10]; int du[N+10],bin[N+10],num; int findx(int x) { int r=x; while(bin[r]!=r) r=bin[r]; int j=x,k; while(j!=r) { k=bin[j]; bin[j]=r; j=k; } return r; } void merge(int x,int y) { int fx=findx(x); int fy=findx(y); if(fx!=fy) bin[fy]=fx; } void creat(Tree &T) { T=(Tree )malloc(sizeof(Node)); T->flag=0; for(int i=0; i<26; i++) T->next[i]=NULL; } int inseart(Tree &T,char *s) { int t,l,flag2=0;; l=strlen(s); Tree p=T; for(int i=0; i<l; i++) { t=s[i]-'a'; if(p->next[t]==NULL) { creat(p->next[t]); flag2=1; } p=p->next[t]; } if(flag2==1) { num++; p->flag=num; return p->flag; } return p->flag; } void delete1(Tree p) { for(int i=0; i<26; i++) { if(p->next[i]) { delete1(p->next[i]); } } free(p); } int main() { Tree T; creat(T); for(int i=0; i<=N; i++) { bin[i]=i; du[i]=0; } num=0; int sum=0; while(scanf("%s%s",a,b)!=EOF) { int tx=inseart(T,a); du[tx]++; int ty=inseart(T,b); du[ty]++; merge(tx,ty); } for(int j=1; j<=num; j++) { if(du[j]%2) sum++; if(sum>2) { printf("Impossible\n"); delete1(T); return 0; } } if(sum==1) printf("Impossible\n"); else { sum=0; //int ss=findx(1); for(int i=1; i<=num; i++) { if(i==bin[i]) sum++;//这题有坑,如果什么不输入直接Crl+Z也是输出"Possible"; } if(sum==1||sum==0) printf("Possible\n"); else printf("Impossible\n"); } delete1(T); return 0; }
解题思路:
可以用图论中欧拉路的知识来解这道题,首先可以把木棒两端看成节点,把木棒看成边,这样相同的颜色就是同一个节点
问题便转化为:
给定一个图,是否存在“一笔画”经过涂中每一点,以及经过每一边一次。
这样就是求图中是否存在欧拉路Euler-Path。
回顾经典的“七桥问题”,相信很多同学马上就明白了什么是 欧拉路 了,这里不多作解释。
由图论知识可以知道,无向图存在欧拉路的充要条件为:
① 图是连通的;
② 所有节点的度为偶数,或者有且只有两个度为奇数的节点。
其中①图的连通性用程序判断比较麻烦,先放一下。
这里先说说②关于度数的判断方法:
|
Blue |
|
Magenta |
|
Violet |
|
Cyan |
|
Red |
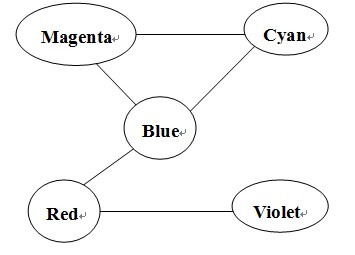
节点的度用颜色出现次数来统计,如样例中,蓝色blue出现三次(不管是出度还是入度),那么blue结点的度就为3,同样地,我们也可以通过输入得到其他全部结点的度,于是,我们有:
Blue=3
Red=2
Violet=1
Cyan=2
Magenta=2
用一个一维数组就能记录了,然后分别 模2,就能判断颜色结点的奇偶性
只要奇度数的结点数的个数 = 1 或 >=3 ,即使①图连通,欧拉路也必不存在
但是若 奇度数的结点数的个数 为0或 ==2,那么我们继续进行①图的连通性证明:
证明①图的连通性,使用并查集MergeSet是非常高效的方法。
知识考查点:
1、字典树;
2、欧拉路:其中又考察了判断是否为连通图;
3、并查集 及其优化方法(路径压缩)。
输出:
POSSIBLE: 奇度数结点个数==0 或 ==2 且 图连通
IMPOSSIBLE:奇度数结点个数==1 或 >=3 或 图不连通


 浙公网安备 33010602011771号
浙公网安备 33010602011771号