POJ3009：Curling 2.0（dfs）

Description

On Planet MM-21, after their Olympic games this year, curling is getting popular. But the rules are somewhat different from ours. The game is played on an ice game board on which a square mesh is marked. They use only a single stone. The purpose of the game is to lead the stone from the start to the goal with the minimum number of moves.

Fig. 1 shows an example of a game board. Some squares may be occupied with blocks. There are two special squares namely the start and the goal, which are not occupied with blocks. (These two squares are distinct.) Once the stone begins to move, it will proceed until it hits a block. In order to bring the stone to the goal, you may have to stop the stone by hitting it against a block, and throw again.

Fig. 1: Example of board (S: start, G: goal)

The movement of the stone obeys the following rules:

At the beginning, the stone stands still at the start square.
The movements of the stone are restricted to x and y directions. Diagonal moves are prohibited.
When the stone stands still, you can make it moving by throwing it. You may throw it to any direction unless it is blocked immediately(Fig. 2(a)).
Once thrown, the stone keeps moving to the same direction until one of the following occurs:
- The stone hits a block (Fig. 2(b), (c)).
  - The stone stops at the square next to the block it hit.
  - The block disappears.
- The stone gets out of the board.
  - The game ends in failure.
- The stone reaches the goal square.
  - The stone stops there and the game ends in success.
You cannot throw the stone more than 10 times in a game. If the stone does not reach the goal in 10 moves, the game ends in failure.

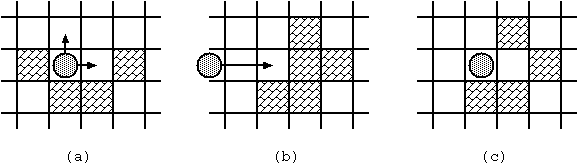Fig. 2: Stone movements

Under the rules, we would like to know whether the stone at the start can reach the goal and, if yes, the minimum number of moves required.

With the initial configuration shown in Fig. 1, 4 moves are required to bring the stone from the start to the goal. The route is shown in Fig. 3(a). Notice when the stone reaches the goal, the board configuration has changed as in Fig. 3(b).

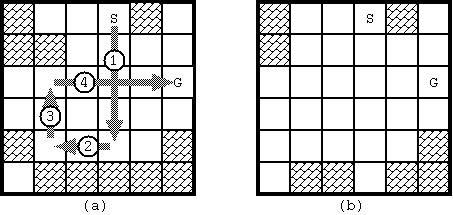Fig. 3: The solution for Fig. D-1 and the final board configuration

Input

The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets never exceeds 100.

Each dataset is formatted as follows.

the width(=w) and the height(=h) of the board First row of the board ... h-th row of the board

The width and the height of the board satisfy: 2 <= w <= 20, 1 <= h <= 20.

Each line consists of w decimal numbers delimited by a space. The number describes the status of the corresponding square.

0 vacant square

1 block

2 start position

3 goal position

The dataset for Fig. D-1 is as follows:

6 6

1 0 0 2 1 0

1 1 0 0 0 0

0 0 0 0 0 3

0 0 0 0 0 0

1 0 0 0 0 1

0 1 1 1 1 1

Output

For each dataset, print a line having a decimal integer indicating the minimum number of moves along a route from the start to the goal. If there are no such routes, print -1 instead. Each line should not have any character other than this number.

Sample Input

2 1
3 2
6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1
6 1
1 1 2 1 1 3
6 1
1 0 2 1 1 3
12 1
2 0 1 1 1 1 1 1 1 1 1 3
13 1
2 0 1 1 1 1 1 1 1 1 1 1 3
0 0

Sample Output

1
4
-1
4
10
-1
题目解析：
  水题一道，半个小时敲完代码了，可之后就陷入了示例答案错误状况中。。。从9:30一直到11:30都没找到
错误，最后一行一行修改，还是没发现错误。。。尼玛啊，只要把全局变量tx,ty定义成局部变量，示例答案
就对了，交上1A，为什么啊？？？不懂啊。。。。，以后尼玛全部定义成局部变量。

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <stdlib.h>
using namespace std;
int map[30][30];
int n,m,minn;
int xx,yy;
int fx[] = {0,0,-1,1} ;
int fy[] = {1,-1,0,0} ;
void dfs(int x,int y,int ans)
{
    int i,tx,ty;
    if(ans>10||ans>=minn) return ;
    for(i=0; i<4; i++)
    {
        tx=x+fx[i];
        ty=y+fy[i];
        if(map[tx][ty]==1)
            continue;
        while(1)
        {
            if(tx>=1&&tx<=n&&ty>=1&&ty<=m)
            {
                if(map[tx][ty]==1)
                {
                    map[tx][ty]=0;
                    dfs(tx-fx[i],ty-fy[i],ans+1);
                    map[tx][ty]=1;
                    break;
                }
                else if(map[tx][ty]==3)
                {
                    if(minn>ans+1)
                        minn=ans+1;
                    break;
                }
            }
            else if(!(tx>=1&&tx<=n&&ty>=1&&ty<=m))
                break;
            tx+=fx[i];
            ty+=fy[i];
        }
    }
    return ;
}
int main()
{
    while(scanf("%d%d",&m,&n)!=EOF)
    {
        minn=11;
        if(m==0&&n==0) break;
        for(int i=1; i<=n; i++)
        {
            for(int j=1; j<=m; j++)
            {
                scanf("%d",&map[i][j]);
                if(map[i][j]==2)
                {
                    xx=i;
                    yy=j;
                    map[i][j]=0;
                }
            }
        }
        dfs(xx,yy,0);
        if(minn==11)
            printf("-1\n");
        else printf("%d\n",minn);
    }
    return 0;
}

题意不难懂，我大致翻译一下：

就是要求把一个冰壶从起点“2”用最少的步数移动到终点“3”

其中0为移动区域，1为石头区域，冰壶一旦想着某个方向运动就不会停止，也不会改变方向（想想冰壶在冰上滑动），除非冰壶撞到石头1 或者到达终点 3

注意的是：

冰壶撞到石头后，冰壶会停在石头前面，此时（静止状态）才允许改变冰壶的运动方向，而该块石头会破裂，石头所在的区域由1变为0. 也就是说，冰壶撞到石头后，并不会取代石头的位置。

终点是一个摩擦力很大的区域，冰壶若到达终点3，就会停止在终点的位置不再移动。

解题思路：

其实与其说这是深搜题，我觉得更像模拟题。。。

要先明确：

0为滑动区域

1为石头区域

2为起点，也是可滑动区域

3为终点，不可滑动区域

（1）起点为“2”，也是一个可滑动的区域，所以标记起点位置之后，可以把起点当做0

（2）注意区分冰壶是运动的还是静止的，若是静止的话，旁边1格有石头是不能走的。

（3）输出冰壶从2到3的最短路，如果最短路的步数大于10（不包括10），视作无法走到终点（其实这是用来剪枝的）

（4）滑动过程中冰壶不允许出界

基于上面的原则，不难发现：

（1）所谓的“走一步”，就是指冰壶从一个静止状态到下一个静止状态，就是说冰壶在运动时经过的“格数”不视作“步数”，也就是说冰壶每次移动的距离都是不定的。

（2）还有就是由于石头会因为冰壶的碰撞而消失，因此冰壶每“走一步”，场地的环境就会改变一次。

（3）基于（2），可以发现本题虽然是要找 “最短路”，但是BFS几乎不可能，因为每“走一步”，场地的状态就要改变一次；而如果该步不满足要求，又要求把场地的状态还原到前一步，这只有DFS能做到。

（4）基于（3），DFS不是BFS，不能简单地用它来找最短路，必须要把所有可能的路一一找出来，再逐一比较它们的步数才能确定最短。但题目值允许1000MS，此时就面临一个超时的问题。所以题目才同时给出“步数超过10则视为失败”的条件，这是用来剪枝的

posted @ 2014-09-20 00:04 人艰不拆_zmc 阅读(277) 评论(0) 编辑收藏举报

刷新页面返回顶部

POJ3009：Curling 2.0（dfs）

公告