POJ3414—Pots(bfs加回溯）

http://poj.org/problem?id=3414

                                      Pots
Time Limit: 1000MS   Memory Limit: 65536K
Total Submissions: 9996   Accepted: 4198   Special Judge

Description

You are given two pots, having the volume of A and B liters respectively. The following operations can be performed:

  1. FILL(i)        fill the pot i (1 ≤ i ≤ 2) from the tap;
  2. DROP(i)      empty the pot i to the drain;
  3. POUR(i,j)    pour from pot i to pot j; after this operation either the pot j is full (and there may be some water left in the pot i), or the pot i is empty (and all its contents have been moved to the pot j).

Write a program to find the shortest possible sequence of these operations that will yield exactly C liters of water in one of the pots.

Input

On the first and only line are the numbers A, B, and C. These are all integers in the range from 1 to 100 and C≤max(A,B).

Output

The first line of the output must contain the length of the sequence of operations K. The following K lines must each describe one operation. If there are several sequences of minimal length, output any one of them. If the desired result can’t be achieved, the first and only line of the file must contain the word ‘impossible’.

Sample Input

3 5 4

Sample Output

6
FILL(2)
POUR(2,1)
DROP(1)
POUR(2,1)
FILL(2)
POUR(2,1)

题目大意：

给出了两个瓶子的容量A,B, 以及一个目标水量C，

对A、B可以有如下操作:

FILL(i)        fill the pot i (1 ≤ i ≤ 2) from the tap;

DROP(i)      empty the pot i to the drain;

POUR(i,j)    pour from pot i to pot j; after this operation either the pot j is full (and there may be some water left in the pot i), or the pot i is empty (and all its contents have been moved to the pot j).

问经过哪几个操作后能使得任意一个瓶子的残余水量为C。

若不可能得到则输出impossible

 

 

 

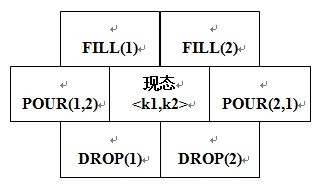
解题思路：
6入口的bfs

把两个两个桶的某个同一时间的状态看做一个整体，视为初态

可对初态进行六种操作，即FILL(1),FILL(2),DROP(1),DROP(2),POUR(1,2),POUR(2,1)

这6种操作在我的程序中分别用一个整数进行记录;

1z0: 清空z瓶子

2z0: 装满z瓶子

3xy: 从x瓶倒向y瓶

（x,y,z∈{1,2}）

这样在输出操作时就能根据数字的特点 进行选择性输出 了

 

最后我简单说说各种操作的数学表达式：

设1瓶的容量为v1，残余水量为k1， 2瓶的容量为v2，残余水量为 k2

那么 fill(1) 相当于 k1=v1  fill(2)相当于k2=v2  drop(1)相当于k1=0   drop(2)相当于k2=0

对于Pour(1,2)，若k1+k2<=v2,则 k2=k1+k2 ， k1=0  （有先后顺序）

               否则k1=k1+k2-v2  ， k2=v2  （有先后顺序）

Pour(2,1)亦同理

利用pre[i]数组来存储当前节点的父节点的位置信息。

之前不会回溯，感到这题无从下手，之后要多做这种题。

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
using namespace std;
int a,b,c,s,e;
int v[101][101];
struct node
{
    int x,y,ans,d,d1;
}q[100001],t,f;
int pre[100001],p[100001];
void FILI(int xx,int yy,int zz,int i,int ff)
{
    if(i==0)
    {
        f.x=a;
        f.y=yy;
        if(v[f.x][f.y]==0)
        {
            f.ans=zz+1;
            f.d=1;
            f.d1=0;
            q[e]=f;
            pre[e]=ff;
            e++;
            v[f.x][f.y]=1;
        }
    }
    else if(i==1)
    {
        f.x=xx;
        f.y=b;
        if(v[f.x][f.y]==0)
        {
            f.ans=zz+1;
            f.d=0;
            f.d1=1;
            q[e]=f;
            pre[e]=ff;
            e++;
            v[f.x][f.y]=1;
        }
    }
}
void POUR(int xx,int yy,int zz,int i,int ff)
{
    if(i==2)
    {
        f.x=0;
        f.y=yy;
        if(v[f.x][f.y]==0)
        {
            f.ans=zz+1;
            f.d=2;
            f.d1=0;
            q[e]=f;
            pre[e]=ff;
            e++;
            v[f.x][f.y]=1;
        }
    }
    else if(i==3)
    {
        f.x=xx;
        f.y=0;
        if(v[f.x][f.y]==0)
        {
            f.ans=zz+1;
            f.d=0;
            f.d1=2;
            q[e]=f;
            pre[e]=ff;
            e++;
            v[f.x][f.y]=1;
        }
    }
}
void D(int xx,int yy,int zz,int i,int ff)
{
    if(i==4)
    {
        if(xx+yy>=a)
        {
             f.x=a;
             f.y=yy+xx-a;
        }
        else
        {
            f.x=xx+yy;
            f.y=0;
        }
        if(v[f.x][f.y]==0)
        {
            f.ans=zz+1;
            f.d=3;
            f.d1=0;
            q[e]=f;
            pre[e]=ff;
            e++;
            v[f.x][f.y]=1;
        }
    }
    else if(i==5)
    {
        if(xx+yy>=b)
        {
             f.y=b;
             f.x=xx+yy-b;
        }
        else
        {
            f.y=xx+yy;
            f.x=0;
        }
        if(v[f.x][f.y]==0)
        {
            f.ans=zz+1;
            f.d=0;
            f.d1=3;
            q[e]=f;
            pre[e]=ff;
            e++;
            v[f.x][f.y]=1;
        }
    }
}
void print(int s)
{
    int ss=0;
    for(int i=s;i!=-1;i=pre[i])
    {
        p[ss++]=i;
    }
    for(int i=ss-1;i>=0;i--)
    {
        if(q[p[i]].d==1||q[p[i]].d1==1)
        {
            if(q[p[i]].d==1)
            {
                printf("FILL(1)\n");
            }
            else printf("FILL(2)\n");
        }
        else if(q[p[i]].d==2||q[p[i]].d1==2)
        {
            if(q[p[i]].d==2)
            {
                printf("DROP(1)\n");
            }
            else printf("DROP(2)\n");
        }
        else if(q[p[i]].d==3||q[p[i]].d1==3)
        {
            if(q[p[i]].d==3)
            {
                printf("POUR(2,1)\n");
            }
            else printf("POUR(1,2)\n");
        }
    }
}
void BFS()
{
    e=0;
    s=0;
    memset(pre,-1,sizeof(pre));
    memset(v,0,sizeof(v));
    v[0][0]=1;
    t.x=0;
    t.y=0;
    t.ans=0;
    t.d=0;
    t.d1=0;
    q[e++]=t;
    while(s<e)
    {
        t=q[s++];
        if(t.x==c||t.y==c)
        {
            printf("%d\n",t.ans);
            print(s-1);
            return ;
        }
        for(int i=0;i<6;i++)
        {
            if(i==0)
            FILI(t.x,t.y,t.ans,i,s-1);
            else if(i==1)
            FILI(t.x,t.y,t.ans,i,s-1);
            else if(i==2)
            POUR(t.x,t.y,t.ans,i,s-1);
            else if(i==3)
            POUR(t.x,t.y,t.ans,i,s-1);
            else if(i==4)
            D(t.x,t.y,t.ans,i,s-1);
            else if(i==5)
            D(t.x,t.y,t.ans,i,s-1);
        }
    }
    printf ("impossible\n");
}
int main()
{
    while(scanf("%d%d%d",&a,&b,&c)!=EOF)
    {
        BFS();
    }
    return 0;
}

 

posted @ 2014-07-29 18:52  人艰不拆_zmc  阅读(1059)  评论(0)  编辑  收藏  举报