基于邻接表存储的图的深度优先遍历和广度优先遍历
一.深度优先遍历是连通图的一种遍历策略。其基本思想如下:
设x是当前被访问顶点,在对x做过访问标记后,选择一条从x出发的未检测过的边(x,y)。若发现顶点y已访问过,则重新选择另一条从x出发的未检测过的边,否则沿边(x,y)到达未曾访问过的y,对y访问并将其标记为已访问过;然后从y开始搜索,直到搜索完从y出发的所有路径,即访问完所有从y出发可达的顶点之后,才回溯到顶点x,并且再选择一条从x出发的未检测过的边。上述过程直至从x出发的所有边都已检测过为止。
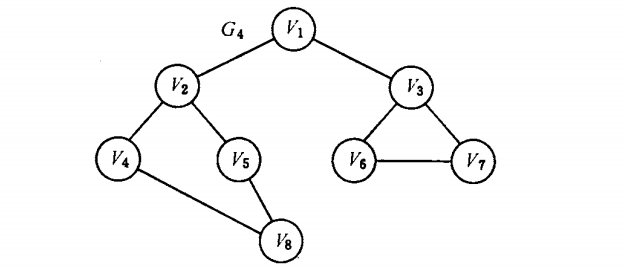
例如下图中:
1.从0开始,首先找到0的关联顶点3
2.由3出发,找到1;由1出发,没有关联的顶点。
3.回到3,从3出发,找到2;由2出发,没有关联的顶点。
4.回到4,出4出发,找到1,因为1已经被访问过了,所以不访问。
所以最后顺序是0,3,1,2,4
二.广度优先遍历是连通图的一种遍历策略。其基本思想如下:

1、从图中某个顶点V0出发,并访问此顶点;
2、从V0出发,访问V0的各个未曾访问的邻接点W1,W2,…,Wk;然后,依次从W1,W2,…,Wk出发访问各自未被访问的邻接点;
3、重复步骤2,直到全部顶点都被访问为止。
例如下图中:
1.从0开始,首先找到0的关联顶点3,4
2.由3出发,找到1,2;由4出发,找到1,但是1已经遍历过,所以忽略。
3.由1出发,没有关联顶点;由2出发,没有关联顶点。
所以最后顺序是0,3,4,1,2
三.下面以此无向图为例,实现深度优先遍历和广度优先遍历:

实现代码如下:
/** 邻接表深度优先遍历和广度优先遍历 **/ #include<stdio.h> #include<stdlib.h> #define MaxVex 255 #define TRUE 1 #define FALSE 0 typedef char VertexType; //顶点类型 typedef int Bool; Bool visited[MaxVex]; //全局数组,记录图中节点访问状态 typedef struct EdgeNode { //边表节点 int adjvex; //该邻接点在顶点数组中的下标 struct EdgeNode *next; //链域 指向下一个邻接点 }EdgeNode; typedef struct VertexNode { //头节点 VertexType data; //顶点信息 EdgeNode *firstedge; //边表头指针(指向第一条依附于该顶点的弧的指针) }VertexNode,AdjList[MaxVex]; //顶点数组(结构体数组) typedef struct Graph{ AdjList adjList; int numVertexes,numEdges; //图中当前的结点数以及边数 }Graph,*GraphAdjList; /** 队列定义及相关操作(广度遍历会用到此循环队列) **/ typedef struct LoopQueue{ int data[MaxVex]; int front,rear; }LoopQueue,*Queue; //队列结构 void initQueue(Queue &Q){ Q->front=Q->rear=0; } Bool QueueEmpty(Queue &Q){ if(Q->front == Q->rear){ return TRUE; }else{ return FALSE; } } Bool QueueFull(Queue &Q){ if((Q->rear+1)%MaxVex == Q->front){ return TRUE; }else{ return FALSE; } } /** * 队尾插入元素 */ void EnQueue(Queue &Q,int e){ if(!QueueFull(Q)){ Q->data[Q->rear] = e; Q->rear = (Q->rear+1)%MaxVex; } } /** * 队头删除元素 */ void DeQueue(Queue &Q,int *e){ if(!QueueEmpty(Q)){ *e = Q->data[Q->front]; Q->front = (Q->front+1)%MaxVex; } } /*************************************************/ /** * 建立图的邻接表结构(此处以无向图为例) */ void CreateALGraph(GraphAdjList &G){ int i, j, k; if(G==NULL){ G = (GraphAdjList)malloc(sizeof(Graph)); } printf("输入图的结点数以及边数: "); scanf("%d%d",&G->numVertexes,&G->numEdges); fflush(stdin); printf("===========================\n"); printf("输入各个顶点的数据:\n"); for (i=0; i<G->numVertexes; ++i){ printf("顶点%d: ",i+1); scanf("%c", &(G->adjList[i].data)); G->adjList[i].firstedge = NULL; fflush(stdin); } printf("===========================\n"); for (k=0; k<G->numEdges; ++k){ printf("输入(vi,vj)上的顶点序号: "); scanf("%d%d",&i,&j); EdgeNode *ptrEdgeNode = (EdgeNode*)malloc(sizeof(EdgeNode)); ptrEdgeNode->adjvex = j; ptrEdgeNode->next = G->adjList[i].firstedge; G->adjList[i].firstedge = ptrEdgeNode; ptrEdgeNode = (EdgeNode*)malloc(sizeof(EdgeNode)); ptrEdgeNode->adjvex = i; ptrEdgeNode->next = G->adjList[j].firstedge; G->adjList[j].firstedge = ptrEdgeNode; } } void DFS(GraphAdjList &G, int i){ visited[i] = TRUE; printf("%c ", G->adjList[i].data); EdgeNode *p = G->adjList[i].firstedge; while(p){ if(!visited[p->adjvex]){ DFS(G,p->adjvex); //递归深度遍历 } p= p->next; } } /** * 深度优先遍历 */ void DFSTraverse(GraphAdjList &G){ int i; for (i=0; i<G->numVertexes; ++i){ visited[i] = FALSE; //初始化访问数组visited的元素值为false } for (i=0; i<G->numVertexes; ++i){ if(!visited[i]){ //节点尚未访问 DFS(G,i); } } } /** * 图的广度优先遍历 */ void BFSTraverse(GraphAdjList &G){ int i; Queue Q = (Queue)malloc(sizeof(LoopQueue)); for (i=0; i<G->numVertexes; ++i){ visited[i] = FALSE; } initQueue(Q); for (i=0; i<G->numVertexes; ++i){ if(!visited[i]){ visited[i] = TRUE; printf("%c ", G->adjList[i].data); EnQueue(Q, i); while (!QueueEmpty(Q)){ DeQueue(Q, &i); EdgeNode *p = G->adjList[i].firstedge; while (p){ if (!visited[p->adjvex]){ visited[p->adjvex] = TRUE; printf("%c ", G->adjList[p->adjvex].data); EnQueue(Q, p->adjvex); } p = p->next; } } } } } /** * 程序入口 */ int main(){ GraphAdjList G = NULL; CreateALGraph(G); printf("\n图的深度优先遍历为: "); DFSTraverse(G); printf("\n图的广度优先遍历为: "); BFSTraverse(G); printf("\n"); return 0; }
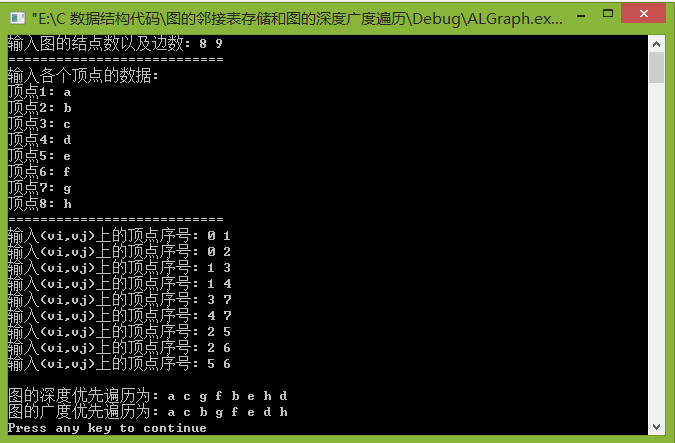
运行结果截图: