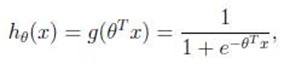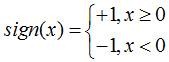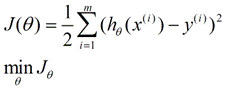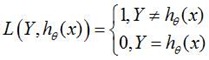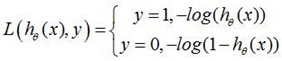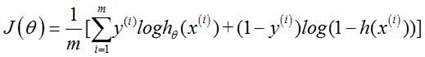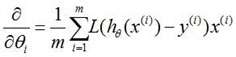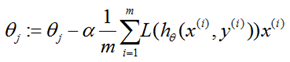logistic回归

1、由线性回归引出的分类问题

   

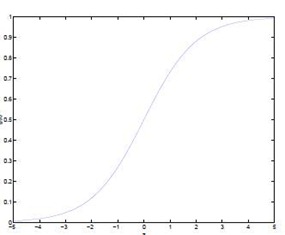
在线性回归中，X定义域为实数集，假设函数(Hypothesis)值域也取值实数集，那么希望有一种假设函数可将取值为实数集特征向量映射到有限的值域。logistic函数：

   

logistic函数可以将取值为特征向量映射到值域(0,1)。

   

关于X特征向量的假设函数

   

那么我们可将有限值域的回归函数通过设定决策边界将之变为判别函数

   

 

2、损失函数

线性回归的损失函数为

   

若假设函数(Hypothesis)为逻辑斯蒂函数，则损失函数的不是一个二次的凸函数，用梯度下降法不能求其的极值，但损失函数不限于一种。统计学习中常用的损失函数有以下几种：

(1)、0-1损失函数(0-1 loss function):

   

(2)、平方损失函数(quadratic loss function)

   

(3)、绝对值损失函数(absolute loss function)

   

(4)、对数损失函数(logarithmic loss function) 或对数似然损失函数(log-likelihood loss function)

   

这里我们使用对数似然损失函数

   

   

对损失函数求偏导我们仍然能得到线性回归假设函数求偏导得到的梯度

   

 

3、梯度下降

repeat until convergence {

   

}

和线性回归相比logistic回归除了假设函数不同以外，其他方面并没有什么不同

 

4、多类问题

判别分类模型通常情况下被描述成二值函数，对二类问题处理没有问题，但问题是如何推广到多类？

对于多类分类问题，可以将其看做成二类分类问题：保留其中的一类，剩下的作为另一类。对于每一个类 i 训练一个由该类别 i 组成正例，其他类别合并组成负例的关于类 i 的分类器，有多少个类，就有多少个分类器。对于一个新的输入变量x，分别对每一个类进行预测，取假设函数返回最优值(极大/极小)的那个类作为分类结果：

   

 

5、其他优化算法

(1)、Conjugate gradient method( 共轭梯度法)

(2)、Quasi-Newton method( 拟牛顿法)

(3)、BFGS method

(4)、L-BFGS(Limited-memory BFGS)