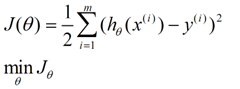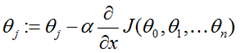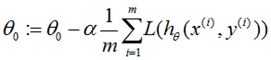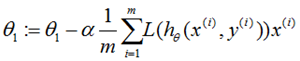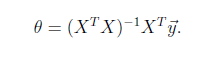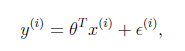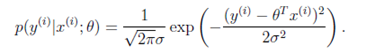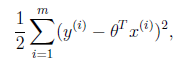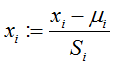线性回归
1、假设模型
线性回归的前置假设是给定的样本模型满足线性关系，即假设的线性模型可以近似的拟合数据
在确定假设模型之后，需要的是对模型函数的参数进行估计，这里是对向量
进行估计
2、损失函数
我们需要一个机制去评估向量θ是否比较好的拟合数据，所以说需要对迭代中的假设模型h进行评估，称为损失函数（loss function），描述h函数与真实数据的误差，我们期望于有某种方法使得误差值最小
3、梯度下降法
目标：
步骤：1、对于每个，给一个初始值，例如都等于0
2、每次改变的时候都保持损失函数J递减，直到达到一个我们满意的最小值；对于任何损失函数J , 初始位置不同，最终达到的极小值点也不同
描述：
repeat until convergence {
}
其中
为学习步长，如果过小，梯度下降可能很慢；如果过大，梯度下降有可能“迈过”（overshoot）最小点，并且有可能收敛失败，并且产生“分歧”(diverge)
如何选择α-经验的方法： ..., 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1...
repeat until convergence {
}
5、最小二乘法
将训练特征表示为X矩阵，结果表示成y向量，仍然是线性回归模型，误差函数不变。那么θ可以直接由下面公式得出
但此方法要求X是列满秩的，而且求矩阵的逆比较慢。
6、选用误差函数为和平方的概率解释
假设根据特征的预测结果与实际结果有误差
，那么预测结果
和真实结果
满足下式：
一般来讲，误差满足平均值为0的高斯分布，也就是正态分布。那么x和y的条件概率也就是
这样就估计了单个样本的误差概率，然而我们期待的是模型能够在全部样本上预测最准，也就是概率积最大。注意这里的概率积是概率密度函数积，连续函数的概率密度函数与离散值的概率函数不同。这个概率积成为最大似然估计。我们希望在最大似然估计得到最大值时确定θ。那么需要对最大似然估计公式求导，对上式求导可得
7、多变量线性回归的特征归一化
目标：使每一个特征值都近似的落在−1≤xi≤1的范围内。
那么简单的归一化，除以每组特征的最大值
均值归一化，用xi−μi替换xi使特征的均值近似为0（但是不对x0=1处理），均值归一化的公式是：
其中Si可以是特征的取值范围（最大值-最小值），也可以是标准差(standard deviation).
8、多项式回归
