Hill密码

本文为转载他人文章

这里主要介绍的是：古典密码之 hill密码加密解密过程的编程实现。

首先，请看对我对hill密码做的简单介绍。

hill密码是古典密码中多表代换密码部分的重要一环，以下的介绍节选自百度，想要深入了解的请查阅书籍补充相关知识。

原理：希尔密码(Hill Password)是运用基本矩阵论原理的替换密码，由Lester S. Hill在1929年发明。每个字母当作26进制数字:A=0, B=1, C=2... 一串字母当成n维向量，跟一个n×n的矩阵相乘，再将得出的结果模26。注意用作加密的矩阵(即密匙)在\mathbb_^n必须是可逆的，否则就不可能译码。只有矩阵的行列式和26互质，才是可逆的。

需要的知识储备：

 

1)线性代数基础知识.

2) 初等数论基础知识.

约定：

       1)希尔密码常使用Z26字母表，在此贴中，我们也以Z26最为字母表进行讲解.在附带源码中有两种字母表选择.

2) 大家都知道最小的质数是2,1 既不是质数也不是合数. 在此我们定义1对任何质数的模逆为其本身.

因为对于任意质数n，有: 1*1 % n = 1 的. 也应该是很好理解的.

过程：

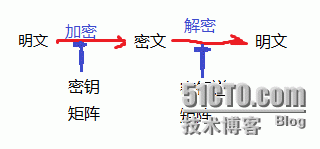
1）加密：密文=明文*密钥矩阵  （注：明文要被分割成与密钥维数相同的一维行列式）
2）解密：明文=密文*密钥矩阵的逆 （注：要求与加密过程相同）

加密解密过程如下图：

wKiom1boxprjDe_VAAAZKXwEiBU284.png

例：

wKioL1box_iQAR_KAABY49UTUXI528.png

wKiom1box_uhu0vvAABDW--g6Ds013.png

加密过程：

wKiom1boyGCShMdqAABOMysHfaA697.png

解密：

wKiom1boyJ6BiUN0AABUhBw0uyc397.png

wKioL1bo0P2A6pBAAAA1WEF6DDQ054.png

对上述过程进行编程，主要的函数声明如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/*
*
*  头文件名称：hillcrypto.h
*  实现文件名称：hillcrypto.cpp
*  项目名称：多表代换密码之hill密码
*  作者：邹明
*  完成时间：2016.3.14
*
*/
 
#ifndef  __HILLCRTPTO_H__
#define __HILLCRTPTO_H__
 
#include<iostream>
using namespace std;
 
#include<assert.h>
#include <iomanip>
 
#define ROW 4  //密钥行数为4
#define COV 4   //密钥列数为4
 
void InputKeys(float keys[ROW][COV]);   //输入密钥
void InputWords(char *words);        //输入明文
void InputObwords(char *words);      //输入密文
void PopKeys(float keys[ROW][COV]);     //输出密钥
void Encryption(float keys[ROW][COV], char *words, char *crypto);   //明文加密
void Decode(float keys[ROW][COV], char *words, char *crypto);     //密文解密
bool Gauss(float A[ROW][COV], float B[ROW][COV], int n);          //高斯消去法求逆矩阵
void   ObMatrix(float a[ROW][COV], float b[ROW][COV], int n);      //求密钥逆矩阵
void menu();   //菜单
 
#endif

 

函数实现过程中的主函数实现以及菜单函数实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
/*   实现文件名称：hillcrypto.cpp    */
#include"hillcrypto.h"
 
int main()
{
    menu();   //菜单+选择
    system("pause");
    return 0;
}
 
void menu()
{
    float keys[ROW][COV] = { 8, 6, 9, 5, 6, 9, 5, 10, 5, 8, 4, 9, 10, 6, 11, 4 };  //加密矩阵（默认密钥）
    float obkeys[ROW][COV] = { 0 };  //解密矩阵 （密钥逆矩阵）
    char words[100] = { 0 };
    char crypto[100] = { 0 };
    char obwords[100] = { 0 };
    bool flag = true;   //菜单选择
    bool chose = false;    //密钥选择
    char cn = 0;
    while (flag)
    {
        int n = 0;
        cout << endl;
        cout << "\t~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~" << endl;
        cout << "\t\t\t1.输入密钥" << endl;
        cout << "\t\t\t2.明文加密" << endl;
        cout << "\t\t\t3.密文解密" << endl;
        cout << "\t\t\t4.退出" << endl << endl;
        cout << "\t~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~" << endl;
        cout << "请选择->：";
        cin >> n;
        switch (n)
        {
        case 1:
            system("cls");
            cout << "默认密钥为："; 
            PopKeys(keys);
            cout << "请问您要重新输入密钥？ y/n" << endl << "请选择->:";
            cin >> cn;
            if ((cn == 'y') || (cn == 'Y'))
            {
                InputKeys(keys);   //输入密钥
            }
            else if ((cn == 'n') || (cn == 'N'))
            {
                cout << "感谢您选择使用默认密钥！" << endl;
            }
            else
                cout << "输入有误，请重新选择！" << endl;
            system("pause");
            break;
        case 2:
            system("cls");
            InputWords(words);  //输入明文
            Encryption(keys, words, crypto);  //加密
            cout << "密文是->：" << crypto << endl;
            system("pause");
            break;
        case 3:
            system("cls");
            InputObwords(crypto);  //输入密文
            ObMatrix(keys, obkeys, COV);  //计算解密矩阵
            Decode(obkeys, obwords, crypto);  //解密
            cout << "明文是->：" << obwords << endl;
            system("pause");
            break;
        case 4:
            system("cls");
            cout << endl << endl << endl;
            cout << setw(15) << "谢谢使用！" << endl;
            flag = false;
            system("pause");
            break;
        default:
            cout << "选择有误，请重新选择！" << endl;
            system("pause");
            break;
        }
    }
}

输入明文函数和输入密文函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
void InputWords(char *words)  //输入明文
{
    assert(words);
    cout << "请输入明文：";
    char *start = words;
    int flag = 1;
    getchar();
    while (flag)
    {
        *words = getchar();
        words++;
        if (*(words - 1) == '\n')
        {
            *words = '\0';
            flag = 0;
        }
    }
    words = start;
    while (*start)
    {
        if (('A' <= *start) && (*start <= 'Z'))
        {
            *words = *start;
            words++;
        }
        else if (('a' <= *start) && (*start <= 'z'))
        {
            *words = *start - 32;
            words++;
        }
        start++;
    }
    *words = '\0';
    cout << "输入成功 ！" << endl;
}
 
void InputObwords(char *words)  //输入密文
{
    assert(words);
    cout << "请输入密文：";
    char *start = words;
    int flag = 1;
    getchar();
    while (flag)
    {
        *words = getchar();
        words++;
        if (*(words - 1) == '\n')
        {
            *words = '\0';
            flag = 0;
        }
    }
    words = start;
    while (*start)
    {
        if (('A' <= *start) && (*start <= 'Z'))
        {
            *words = *start;
            words++;
        }
        else if (('a' <= *start) && (*start <= 'z'))
        {
            *words = *start - 32;
            words++;
        }
        start++;
    }
    *words = '\0';
    cout << "输入成功 ！" << endl;
}

输入密钥与输出密钥函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void InputKeys(float keys[ROW][COV])  //输入密钥
{
    cout << "请输入密钥：" << endl;
    for (size_t i = 0; i < ROW; i++)
    {
        cout << "请输入第" << i << "行密钥("<<ROW<<"个数):";
        for (size_t j = 0; j < COV; j++)
        {
            cin >> keys[i][j];
        }
    }
    cout << "输入成功 !" << endl;
}
 
void PopKeys(float keys[ROW][COV])  //输出密钥
{
    cout << "密钥为：" << endl;
    for (size_t i = 0; i < ROW; i++)
    {
        for (size_t j = 0; j < COV; j++)
        {
            cout << keys[i][j] << "   ";
        }
        cout << endl;
    }
}

加密函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void Encryption(float keys[ROW][COV], char *words, char *crypto)  //加密函数
{
    assert(words);
    int len = strlen(words);
    char *start = words;
 
    while (len > 0)
    {
        int matrix[ROW] = { 0 };
        for (int i = 0; i < ROW; i++)
        {
            if (*start)
                matrix[i] = *start - 'A';
            else
                matrix[i] = 0;
            start++;
        }
        len -= ROW;
        int cry[ROW] = { 0 };
        for (int i = 0; i < ROW; i++)
        {
            int temp = 0;
            for (int j = 0; j < COV; j++)
            {
                temp = matrix[j] * keys[j][i] + temp;
            }
            cry[i] = temp % 26;
            *crypto = 'A' + cry[i];  //计算密文
            crypto++;
        }
    }
}

解密函数，以及求逆矩阵函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
void Decode(float obkeys[ROW][COV], char *words, char *crypto)//解密函数
{
    assert(crypto);
    int len = strlen(crypto);
    char *start = crypto;
    while (len > 0)
    {
        int matrix[ROW] = { 0 };
        for (int i = 0; i < ROW; i++)
        {
            if (*start)
                matrix[i] = *start - 'A';
            else
                matrix[i] = 0;
            start++;
        }
        len -= ROW;
        int cry[ROW] = { 0 };
        for (int i = 0; i < ROW; i++)
        {
            int temp = 0;
            for (int j = 0; j < COV; j++)
            {
                temp = matrix[j] * obkeys[j][i] + temp;
            }
            cry[i] = temp % 26;
            *words = 'A' + cry[i];  //计算明文
            words++;
        }
    }
}
 
void   ObMatrix( float a[ROW][COV], float b[ROW][COV], int n)  //求逆矩阵函数
{
        int i, j;         //定义矩阵的行列式
    if (Gauss(a, b, n))
    {
        cout << "该方阵的逆矩阵为: \n";
        for (i = 0; i < n; i++)
        {
            cout << setw(4);
            for (j = 0; j < n; j++)
            {
                int temp =b[i][j]/ 1;
                float num = b[i][j] - temp;
                if (fabs(num) < 0.50)
                    b[i][j] = (int)temp;
                else
                    b[i][j] = temp + (int)(num * 2);
                cout << b[i][j] << setw(10);
            }
            cout << endl;
        }
    }
    cout << "逆矩阵（mod26）:" << endl;
    for (int i = 0; i < ROW; i++)
    {
        cout << setw(4);
        for (int j = 0; j < COV; j++)
        {
            if (b[i][j] >= 0)
            {
                b[i][j] = (int)b[i][j] % 26;
            }
            else
            {
                b[i][j] = 26 + (int)b[i][j] % 26;
            }
            cout << b[i][j] << setw(6);
        }
        cout << endl;
    }
 
}
 
 
bool Gauss(float A[ROW][COV], float B[ROW][COV], int n) //高斯消去法
{
    int i, j, k;
    float max, temp;
    float t[ROW][COV];                //临时矩阵
    //将A矩阵存放在临时矩阵t[n][n]中
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < n; j++)
        {
            t[i][j] = A[i][j];
        }
    }
    //初始化B矩阵为单位阵
    for (i = 0; i < n; i++)
    {
        for (j = 0; j < n; j++)
        {
            B[i][j] = (i == j) ? (int)1 : 0;
        }
    }
    for (i = 0; i < n; i++)
    {
        //寻找主元
        max = t[i][i];
        k = i;
        for (j = i + 1; j < n; j++)
        {
            if (fabs(t[j][i]) > fabs(max))
            {
                max = t[j][i];
                k = j;
            }
        }
        //如果主元所在行不是第i行，进行行交换
        if (k != i)
        {
            for (j = 0; j < n; j++)
            {
                temp = t[i][j];
                t[i][j] = t[k][j];
                t[k][j] = temp;
                //B伴随交换
                temp = B[i][j];
                B[i][j] = B[k][j];
                B[k][j] = temp;
            }
        }
        //判断主元是否为0, 若是, 则矩阵A不是满秩矩阵,不存在逆矩阵
        if (t[i][i] == 0)
        {
            cout << "There is no inverse matrix!";
            return false;
        }
        //消去A的第i列除去i行以外的各行元素
        temp = t[i][i];
        for (j = 0; j < n; j++)
        {
            t[i][j] = t[i][j] / temp;        //主对角线上的元素变为1
            B[i][j] = B[i][j] / temp;        //伴随计算
        }
        for (j = 0; j < n; j++)        //第0行->第n行
        {
            if (j != i)                //不是第i行
            {
                temp = t[j][i];
                for (k = 0; k < n; k++)        //第j行元素 - i行元素*j列i行元素
                {
                    t[j][k] = t[j][k] - t[i][k] * temp;
                    B[j][k] = B[j][k] - B[i][k] * temp;
                }
            }
        }
    }
    return true;
}

程序运行结果：

wKioL1bozYHDHhlNAAAgPVqMJxk248.png

选择：1

wKiom1bozY7Bl8wjAAAftuVnUPQ208.png

选择：y

wKiom1bozgDA25DfAAAiYiG2Ohk216.png

选择：n

wKiom1bozlSRqoLeAAAhtOqSI9U425.png

选择 2.明文加密：

wKiom1bozs_gpwobAAAej9bk6zA287.png

选择 3.密文解密：

wKioL1boz8vSv20WAAAmikEJ8Qw938.png

选择 4.退出：

wKiom1boz3ezokj0AAAdJ8dnSG0186.png

 

posted @ 2017-07-12 21:17  寂地沉  阅读(2280)  评论(0)  编辑  收藏  举报