吴恩达老师机器学习课程学习--课时十三
课时十三 聚类
聚类算法也是非监督学习算法,本课时介绍了其中的一种K-Means算法。
1、K-均值算法
K-均值算法是一个迭代算法,算法思想如下:
假如我们要把数据分成n组,方法是:
1:选取K个点,作为聚类中心。
2:对于每一个数据,按照距离K个聚类中心的距离,把它与距离最近的聚类中心关联起来,这样就把数据集中的所有数据按照不同的聚类中心关联成了一类。
3:计算每一类的平均值,然后把该类的聚类中心移到平均值的位置。
4:重复2-3步,直到聚类中心不再改变。

算法包括两步:第一个for循环是对每一个样例,计算它属于的类。第二个for循环是聚类中心的移动。
2、代价函数
K-Means算法的最小化问题,是要最小化所有数据点和与其所关联的聚类中心点之间的距离之和。因此K-均值的代价函数(又称畸变函数)为:
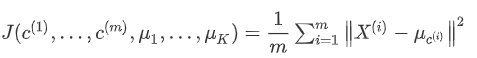
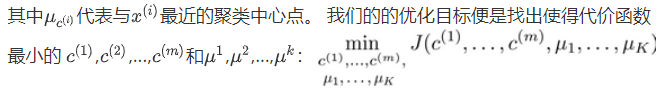
3、随机初始化
在运行K-均值算法之前,我们要随机初始化所有的聚类中心点。做法:
1.随机选择K<m,即聚类中心点的个数小于样本实例的总数
2.随机选择K个训练实例,然后让这K个训练实例作为聚类中心
K-均值有一个问题,就是它可能会停留在局部最小值,这取决于初始化的情况,为了解决这个问题,我们通常需要多次运行K-均值算法,每一次都重新进行随机初始化,最后再比较多次运行的K-均值的结果,选择代价函数最小的结果。这种方法在K较小的时候(2-10)是比较管用的,但是如果K比较大,这么做也可能不会有明显的改善。
4、选择聚类数
没有所谓的最好的选择聚类数的方法,通常是根据实际问题,人工进行选择。老师介绍了一种肘部法则的方法:通过不停地改变聚类数,运行K-均值算法,得出代价函数,然后会得到下面这张图:
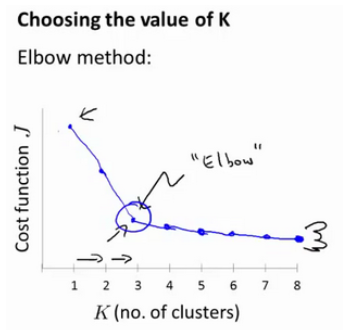
像一个人的肘部。这就是“肘部法则”所做的,让我们来看这样一个图,看起来就好像有一个很清楚的肘在那儿。好像人的手臂,如果你伸出你的胳膊,那么这就是你的肩关节、肘关节、手。这就是“肘部法则”。你会发现这种模式,它的畸变值会迅速下降,从1到2,从2到3之后,你会在3的时候达到一个肘点。在此之后,畸变值就下降的非常慢,看起来就像使用3个聚类来进行聚类是正确的,这是因为那个点是曲线的肘点,畸变值下降得很快,K=3之后就下降得很慢,那么我们就选K=3。
上面就是本节课时的内容,课程笔记部分来自:“机器学习初学者”网站提供的吴恩达老师的2014机器学习课程笔记http://www.ai-start.com/



