python机器学习——BP（反向传播）神经网络算法

背景与原理：

BP神经网络通常指基于误差反向传播算法的多层神经网络，BP算法由信号的前向传播和反向传播两个过程组成，在前向传播的过程中，输入从输入层进入网络，经过隐含层逐层传递到达输出层输出，如果输出结果与预期不符那么转至误差反向传播过程，否则结束学习过程。在反向传播过程中，误差会基于梯度下降原理分配给各层神经元，修正各个神经元的权值。

考虑一个经典的分类问题，假设我们有一组数据形如$(x_{1},...,x_{n},y)$，其中$y$为这个数据所属的类别，不妨设有$k$个取值$(C_{1},...,C_{k})$，那么重复之前的描述：我们实际上要求的是给定了一个输入$X$，求这个输入属于某一类的概率，也就是说我们可以理解为输入一个$n$维向量，希望预测一个$k$维向量，每一维表示这个输入属于这一类的概率，而最后我们的预测结果就是概率最大的那一个维度。

考虑一个基础的逻辑回归，我们构造了一个线性函数$z=w^{T}x+b$，然后令$g(z)=\dfrac{1}{1+e^{-z}}$，这样$g(z)$就可以用来表示一个0-1二分类问题中属于类别1的概率。

而这个函数的意义，一方面在于将$R$光滑对称地映射到了$(0,1)$区间能有效地表示概率，另一方面，linear的东西始终只是linear的，当然我们可以引入多项式特征解决一定的问题，但这样我们要面对的问题就是——究竟引入多少才算合适？而这个sigmoid函数能够把linear的东西变成non-linear的，这就是一个进步。

而如果从神经网络的生物学背景来看，我们会看到一个神经元一般有两个状态，即静息状态和兴奋状态，而我们的人工神经网络从背景上来说是对人类神经系统行为的一种模拟，因此一个取值在$[0,1]$之间的函数可以看做神经元状态的一个反映——0代表静息状态，1代表兴奋状态，所以在神经网络中，类似于sigmoid这样的函数是很常用的，它们被称作激活函数。

那么说了这么多，神经网络究竟是在干什么呢？

从一定的意义上来说，神经网络实际上实现的是函数的不断复合——虽然即使引入了一个sigmoid函数，linear的东西可能还是无法摆脱linear，那我们就再设法复合上一层，这样它就没有那么linear了，以此类推，当我们复合次数足够多的时候，我们得到的最终结果将能够拟合出这个“客观正确”的预测模型。

这个过程是怎么实现的呢？

首先神经网络被分为三个部分：输入层、隐藏层和输出层，每层有若干个节点，每个节点称为一个神经元，输入层有$n$个节点，对应于输入特征的维度，输出层有$k$个节点，对应于要预测的东西的维度。

而我们首先从单隐藏层的结构开始：假设我们只有一个隐藏层，这个隐藏层上有$n_{1}$个节点，那么第$i$个节点要处理的输入上一层的所有输入，对于这第一个隐藏层就是$x_{1},...,x_{n}$，而后计算出$z_{i}=w_{i}^{T}x+b$（即输入的一个线性函数），然后用自己的激活函数处理这个信号并发出，即第$i$个节点的输出是$f_{i}(z_{i})$

那么这个过程实际上就是对人类神经元活动的一种模拟：神经元接受上一个神经元发来的信号——神经元处理信号产生一个神经冲动传递给下一个神经元

那么我们假设只有一个隐藏层，那么这个隐藏层的输出就是$f_{1}(z_{1}),...,f_{n_{1}}(z_{n_{1}})$，而下一个就到了输出层，即输出层的第$j$个神经元输出的就是$f_{d}(\omega_{j}^{T}f(z)+\beta_{j})$（无需在意符号，只是为了区分各个层的参数）

那么非常自然地，如果我们有很多个隐藏层，对于第二个隐藏层而言，其接受的输入就是第一个隐藏层的输出，以此类推，每个神经元还是按照自己的参数将上一层的输出线性组合后扔进自己的激活函数里输出给下一层，直到到达输出层为止。

那么实际上，对于一个全连接神经网络，假设上一层有$n$个神经元，下一层有$m$个神经元，上一层第$j$个神经元的输出是$a_{j}$，那么下一层第$i$个神经元的输入是$\sum_{j=1}^{n}w_{ij}a_{j}+b_{i}$

那么如果设下一层是第$d$层，上一层是第$d-1$层，这样下一层的输入是上一层的输出的一个线性组合，记为$z_{d}$，我们有：

$z_{d}=\begin{pmatrix} z_{1} \\ z_{2} \\ ... \\ z_{m} \end{pmatrix}=\begin{pmatrix} \sum_{j=1}^{n}w_{1j}a_{j}+b_{1} \\ \sum_{j=1}^{n}w_{2j}a_{j}+b_{2} \\ ... \\ \sum_{j=1}^{n}w_{mj}a_{j}+b_{m} \end{pmatrix}=\begin{pmatrix} w_{11} & w_{12} & ... & w_{1n} \\ w_{21} & w_{22} &.. & w_{2n}\\...\\w_{m1} & w_{m2} &...& w_{mn}\end{pmatrix} \begin{pmatrix} a_{1}\\a_{2}\\...\\a_{n} \end{pmatrix} + \begin{pmatrix} b_{1}\\b_{2} \\...\\b_{m}\end{pmatrix}$

 这样我们设$W_{d}=\begin{pmatrix} w_{11} & w_{12} & ... & w_{1n} \\ w_{21} & w_{22} &.. & w_{2n}\\...\\w_{m1} & w_{m2} &...& w_{mn}\end{pmatrix}$，而$a_{d-1}=\begin{pmatrix} a_{1}\\a_{2}\\...\\a_{n} \end{pmatrix}$，$b_{d}=\begin{pmatrix} b_{1}\\b_{2} \\...\\b_{m}\end{pmatrix}$

这样我们有$z_{d}=W_{d}a_{d}+b_{d}$，而第$d$层的输出，也即第$d+1$层的输入就是$a_{d}=f_{d}(z_{d})$

这样的就构成了一个神经网络，如果每一个神经元的激活函数选的足够好，参数也训练的足够好，再忽略可能的过拟合问题，那么这个神经网络的表现应该是很不错的。

但是...等等，这样的神经网络要怎么训练啊！

这个问题是巨大的——假设我们的神经网络每层有10个神经元，而我们一共有10个隐藏层，这样就需要100个神经元，而每个神经元要对前一层10个神经元的输出做一个线性组合，这就需要11个参数，也就是说这样一个“简陋”的神经网络我们就要训练足足1100个参数（粗略估计，并不严格）！

那么如果没有一个合适的方法，训练神经网络的开销将是灾难性的。

幸运的是，回忆一开始的梯度下降方法，我们知道如果我们希望让一个函数尽快到达最低点，我们只需按照一定的步长沿下降最快的方向前进即可，那么在这里是不是也可以引入类似的方法呢？

在神经网络中我们需要的参数主要有$w,b$，那么我们定义一个损失函数$J(w,b)$，那如果我们能求出一个梯度$\dfrac{\partial J}{\partial w_{i}}$，那我们当然可以按照梯度下降的方法更新$\hat{w_{i}}=w_{i}-\alpha \dfrac{\partial J}{\partial w_{i}}$

但是很遗憾的是，由于函数复合的复杂性，我们想要计算出一个损失函数对某个具体的$w_{i}$的偏导数是相当困难的，因为这个$w_{i}$可能前面复合了一堆东西，后面又复合上了一堆东西，想要直接计算出这个偏导数是另一场灾难。

幸运的是，我们可以从另一个角度来思考这个问题：我们从输出层向前来考虑，假设输出为一个列向量$a_{D}$，而这个$a_{D}$满足$a_{D}=f_{D}(w_{D}a_{D-1}+b_{D})$，那么我们可以很自然地看到：

$\dfrac{\partial J}{\partial w_{D}}=\dfrac{\partial J}{\partial z_{D}} \dfrac{\partial z_{D}}{\partial w_{D}}=\dfrac{\partial J}{\partial z_{D}} a_{D-1}$

$\dfrac{\partial J}{\partial b_{D}}=\dfrac{\partial J}{\partial z_{D}} \dfrac{\partial z_{D}}{\partial b_{D}}=\dfrac{\partial J}{\partial z_{D}}$

而$a_{D-1}$是已知，我们实际要求出：

$\dfrac{\partial J}{\partial z_{D}}$

当然，这个是不难求解的，求解的结果与损失函数有关，我们不妨设这个东西是$\delta_{D}=\dfrac{\partial J}{\partial z_{D}}$

那我们再往前求，如果我们想求出$\dfrac{\partial J}{\partial w_{d}}$，那么由复合函数求导法则，我们有：

$\dfrac{\partial J}{\partial w_{d}}=\dfrac{\partial J}{\partial z_{D}}\dfrac{\partial z_{D}}{\partial z_{D-1}}...\dfrac{\partial z_{d+1}}{\partial z_{d}}\dfrac{\partial z_{d}}{\partial w_{d}}$

而我们知道$\dfrac{\partial z_{d}}{\partial w_{d}}=a_{d-1}$，因此我们有：

$\dfrac{\partial J}{\partial w_{d}}=\dfrac{\partial J}{\partial z_{D}}\dfrac{\partial z_{D}}{\partial z_{D-1}}...\dfrac{\partial z_{d+1}}{\partial z_{d}}a_{d-1}$

这样我们设$\delta_{d}=\dfrac{\partial J}{\partial z_{d}}$，那么我们始终有：

$\dfrac{\partial J}{\partial w_{d}}=\delta_{d} a_{d-1}$

而$\delta_{d}=\dfrac{\partial J}{\partial z_{D}}\dfrac{\partial z_{D}}{\partial z_{D-1}}...\dfrac{\partial z_{d+1}}{\partial z_{d}}$，那么我们有递推：

$\delta_{d}=\delta_{d+1}\dfrac{\partial z_{d+1}}{\partial z_{d}}$

而我们需要算出的是$\dfrac{\partial z_{d+1}}{\partial z_{d}}$

而我们知道$z_{d+1}=w_{d+1}f(z_{d})+b_{d+1}$，这样我们有：

$\dfrac{\partial z_{d+1}}{\partial z_{d}}=\dfrac{\partial z_{d+1}}{\partial f_{d}(z_{d})}\dfrac{\partial f_{d}(z_{d})}{\partial z_{d}}$

因此我们最后得到：

$\dfrac{\partial z_{d+1}}{\partial z_{d}}=w_{d+1}f_{d}^{'}(z_{d})$

因此我们得知：当前层的梯度应该等于回传回当前层的梯度（$\delta_{d+1}$）乘以当前层的导数再乘以上一层的输入。

那么我们总结一下BP神经网络的流程：

首先要确定输入、输出和损失函数，然后选取神经网络的结构（层数、每层的神经元个数、每层的激活函数、学习率），然后按照上述过程训练至收敛就好。

代码实现：

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import LinearSVC
import matplotlib.pyplot as plt
import pylab as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
import tensorflow as tf
from sklearn.neural_network import MLPClassifier


X,y=datasets.make_classification(n_samples=1000,n_features=20,n_informative=2,n_redundant=2)
X_train,X_test,Y_train,Y_test=train_test_split(X,y,test_size=0.25)

lr=LogisticRegression()
svc=LinearSVC(C=1.0)
rfc=RandomForestClassifier(n_estimators=100)#森林中树的个数

lr=lr.fit(X_train,Y_train)
score1=lr.score(X_test,Y_test)
print(score1)

svc=svc.fit(X_train,Y_train)
score2=svc.score(X_test,Y_test)
print(score2)

rfc=rfc.fit(X_train,Y_train)
score3=rfc.score(X_test,Y_test)
print(score3)

gnb=GaussianNB()
gnb=gnb.fit(X_train,Y_train)
score4=gnb.score(X_test,Y_test)
print(score4)


sc=[]
siz=[]
i=5
while i<=100:
    clf = MLPClassifier(solver='lbfgs', alpha=1e-5,activation='logistic',
                    hidden_layer_sizes=(i,i), random_state=1,max_iter=500000)
    clf.fit(X_train, Y_train)
    sc.append(clf.score(X_test,Y_test))
    siz.append(i)
    i+=5
plt.plot(siz,sc,c='r')
plt.show()

这段代码使用sklearn自带的简易神经网络分类器来训练一个模型，其中solver这个参数指定了梯度下降的方式，alpha指定了正则化参数，activation指定了激活函数，hidden_layer_sizes是一个元组，每一项对应于一个隐藏层中神经元的个数，max_iter决定了神经网络最大的迭代次数，超过这个次数的话会返回一个错误

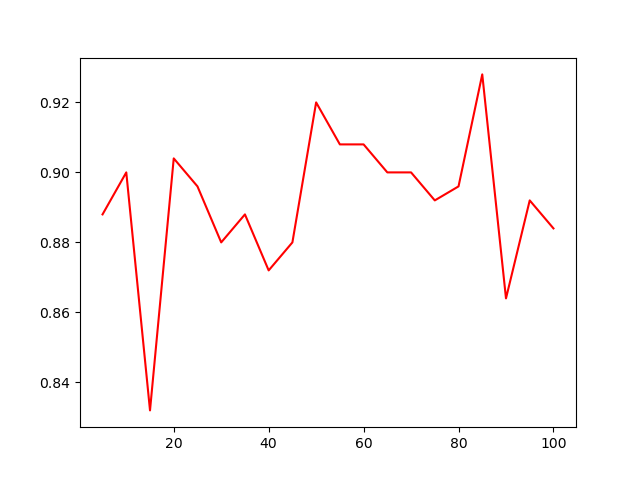
这是这个两个隐藏层的神经网络在这组数据上的表现随每层神经元个数变化的图像

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import LinearSVC
import matplotlib.pyplot as plt
import pylab as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
from sklearn.neural_network import MLPClassifier


X,y=datasets.make_classification(n_samples=1000,n_features=20,n_informative=2,n_redundant=2)
X_train,X_test,Y_train,Y_test=train_test_split(X,y,test_size=0.25)

Y_train=np.array(Y_train).reshape(750,1)
Y_test=np.array(Y_test).reshape(250,1)

def add_layer(input, in_size, out_size, activation_function=None):
    w = tf.Variable(tf.random_normal([in_size, out_size]))
    b = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    Z = tf.matmul(input, w) + b
    if activation_function == None:
        output = Z
    else:
        output = activation_function(Z)
    return output


xs = tf.compat.v1.placeholder(tf.float32, [None, 20])
ys = tf.compat.v1.placeholder(tf.float32, [None, 1])


hidden_layer1 = add_layer(xs, 20, 10, activation_function=tf.nn.relu)
hidden_layer2 = add_layer(hidden_layer1,10,10,activation_function=tf.nn.relu)

prediction = add_layer(hidden_layer2, 10, 1, activation_function=None)


loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction), reduction_indices=[1]))

train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
for i in range(1000):
    sess.run(train_step, feed_dict={xs: X_train, ys: Y_train})
    if i % 100 == 0:
        print(sess.run(loss, feed_dict={xs: X_test, ys: Y_test}))

sess.close()

这是用tensorflow搭建神经网络的一个方法，首先我们需要自定义一个函数叫做add_layer，这个函数输入的参数是而上一层是谁，上一层的神经元个数，本层神经元个数，和本层的激活函数

而每层的初始值可以设成随机值，这里的$w$设计成了一个矩阵，因为对于上一层的第$i$个神经元和本层的第$j$个神经元而言对应的$w$值其实就是$w_{ij}$，而如果我们把一整层看做一个向量的话那么两层之间的线性变换过程实际就是一个矩阵乘法，最后根据激活函数进行下激活就完成了这一层的任务。

而初始我们需要定义两个占位符xs和ys表示输入和输出，第一维是None，第二维表示维度

接下来我们可以定义一些隐藏层和一个输出层，以及一个损失函数，这里按照参考格式写就好。

而反向传播的过程不需要我们来写，TensorFlow提供一个train的包，可以决定按什么方法进行优化，而参数是学习率，后面的minimize是我们要最小化的那个损失函数。

最后我们用tensorflow里的一个叫Session的对象run这个神经网络，就可以实现训练的功能了。

小结与提高：

反向传播神经网络是最简单的神经网络，在很多任务上表现优越，但其也有很多问题，比如模型的可解释性很差——事实上整个神经网络虽然原理清晰，但真实过程就像一个黑盒，比如上面我们会看到模型的表现随神经元个数在震荡，这样的现象并不容易找到一个简单的解释。同时由于超参数很多，如何选取就成了一个大问题，同时由于模型的复杂性导致很容易出现过拟合的现象，同时模型的复杂还会带来训练成本的大幅上升，这些都是神经网络所要面对的大问题。