python机器学习——随机森林算法

背景与原理：

首先我们需要知道集成学习的概念，所谓集成学习，就是使用一系列学习器进行学习，并且通过某种规则把这些学习器的学习结果整合起来从而获得比单个学习器学习效果更好的机器学习方法。这样的方法可以用于解决单个学习器的过拟合、性能瓶颈等问题，常用的集成方式主要有Bagging（并行）和Boosting（串行），随机森林就是Bagging的一种扩展变体。

传统意义上的随机森林算法是基于决策树的集成学习方法，在数据量比较大时决策树会出现性能瓶颈，而随机森林以决策树为基分类器，其由多个由Bagging集成学习技术训练得到的决策树，当输入待分类样本时，最终的分类结果由单个决策树的输出结果投票决定，这样的随机森林解决了性能瓶颈问题、对噪声有较好的容忍度，高度并行且泛化性能较好；同时其还是非参数驱动的分类方法，并不需要对样本的先验知识。

随机森林算法的第一步是构建数据集，假设我们的随机森林由$k$棵决策树组成，那么我们就要从原始数据集中生成$k$个数据集，使用的抽样方法称为Bootstrap方法，是一种随机的有放回抽样。

而对于每个数据集，我们都需要构建一棵决策树，这里我们使用CART，全名为Classification and Regression Tree，即这种树既可以用于分类问题，也可以用于回归问题（即连续值的预测）（值得注意的是这种树每个节点至多有两个分支）

CART回归树：

回顾一下，所谓回归问题就是给定一组数据，每个数据形如$(x_{1},...,x_{n},y)$，现想要训练一个模型$f$实现在已知$X$的情况下对$y$进行预测。

而回归树是怎么操作呢？我们看到这组数据有$n$个特征，我们从中选取一个特征，不妨设为第$i$个特征吧，然后选定一个分界点$p$，然后做一个非常简单粗暴的预测：如果$x_{i}<p$，那么我们就预测满足这样条件的$f(X)=y_{1}$，否则我们预测$f(X)=y_{2}$，这就是最基础的一个树形结构

因为我们的观点是如果数据集中两个数据点足够接近，那么这两个数据点对应的$y$值应该也很接近，所以如果我们把这些数据点划分的足够细，我们就可以认为此时还被划分在一起的点的值可以近似看做相等了。

当然，为了准确性，假设此时被划分在一起的点对应的值为$y_{1},..,y_{k}$，那么我们的预测值应该是$\hat{y}=\dfrac{\sum_{i=1}^{k}y_{i}}{k}$

而我们的回归树的构建就是不断选取一个特征，找到一个划分点把数据划分成几个部分，直到我们认为误差在可以接受的范围内为止。

而我们度量准确性的方法也是非常自然的MSE损失函数，即$J=\dfrac{1}{m}\sum_{i=1}^{m}(f(X_{i})-y_{i})^{2}$

于是现在的问题就变成了：在每个节点上，我们要选取一个特征和一个分界点把这个节点上的数据集分成两部分，如何选取呢？

这个选取方式直观来讲就是遍历所有特征和分界点，每个特征和分界点都会把这个数据集分成两部分，那么我们如果不再向下划分，这两部分的预测值就分别是每个部分的真实值的平均，那么我们有了预测值，自然可以计算出损失函数，而我们选取的特征和分界点应该是使得损失函数值最小的那个！

因此我们重复这个过程就可以构造出一个回归树了。

CART分类树：

这个分类树与前一篇博客所述的决策树有少许不同，这里我们并不使用信息增益，而是使用基尼系数（GINI）作为特征划分点的依据。

基尼系数：在分类问题中，对于一个有$k$个类的数据集$D$，其基尼系数$GINI(D)=\sum_{i=1}^{k}p_{i}(1-p_{i})=1-\sum_{i=1}^{k}p_{i}^{2}$，其中$p_{i}$是属于第$i$类的数据在数据集中的占比。

那么基尼系数越大，说明样本纯度越低，如果想追求比较好的分类效果，我们希望分类到最后的叶节点时基尼系数尽可能低，这样我们如果选了某个特征和划分点将数据集$D$划分为$D_{1},D_{2}$两部分，那么这里的基尼系数可以写作$GINI=\dfrac{|D_{1}|}{|D|}GINI(D_{1})+\dfrac{|D_{2}|}{|D|}GINI(D_{2})$，即两部分的基尼系数的加权平均，这样我们找到使这个基尼系数最小的特征和划分点将数据集分裂，重复这一过程直至取得较好效果即可。

在建立了$k$棵决策树之后，我们通过这$k$棵决策树的多数投票（如果是随机问题，可以按某种加权平均）来得到最终的分类（回归）结果即可。

代码实现：

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import LinearSVC
import matplotlib.pyplot as plt
import pylab as plt
from sklearn.model_selection import train_test_split


X,y=datasets.make_classification(n_samples=10000,n_features=20,n_informative=2,n_redundant=2)
X_train,X_test,Y_train,Y_test=train_test_split(X,y,test_size=0.25)

lr=LogisticRegression()
svc=LinearSVC(C=1.0)
rfc=RandomForestClassifier(n_estimators=100)#森林中树的个数

lr=lr.fit(X_train,Y_train)
score1=lr.score(X_test,Y_test)
print(score1)

svc=svc.fit(X_train,Y_train)
score2=svc.score(X_test,Y_test)
print(score2)

rfc=rfc.fit(X_train,Y_train)
score3=rfc.score(X_test,Y_test)
print(score3)

x=[]
sc=[]
for i in range(1,101):
    rfc = RandomForestClassifier(n_estimators=i)
    rfc = rfc.fit(X_train, Y_train)
    sc.append(rfc.score(X_test, Y_test))
    x.append(i)

plt.plot(x,sc,c='r')
plt.show()

这段代码对比了常用的三种分类器的表现：逻辑回归、支持向量机和随机森林，使用了sklearn的一个数据生成器，同时还展示了随机森林的表现随森林中树的个数的变化。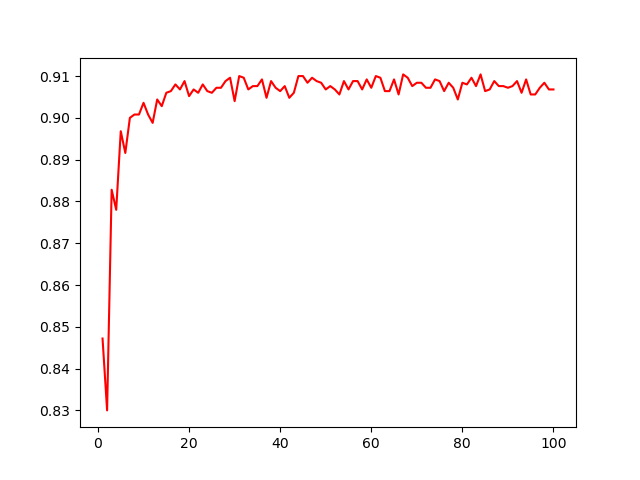

变化图形如上所示，可以看到事实上选择20棵左右的树就已经能有相当不错的表现了，因此随机森林中树的个数选择一定要注意，如果选择的树过多不仅不会使预测效果有明显提高，反而会大大提高模型训练的开销。