bzoj 4660

三倍经验...（然而我并没有氪金所以只能刷一倍...）

考虑在什么情况下两点是合法的：

可以看到，对于红色的点而言，绿色的点是合法的，而黄色的点是不合法的

那么观察一下这几个点的切线把圆分成的这几个弧之间的关系，可以看到：如果两个弧相交但不包含，那么对应的两点合法（比如红色和绿色），剩余情况均不合法！

于是问题就转化成了圆上有很多段弧，求最多有多少个弧之间两两相交不包含

环上的东西不好做，我们考虑在线段上讨论这个问题

依据弧度制，可以把环上两点对应的圆心角弧度映射到一个数轴上，就变成了区间之间的问题了

映射方法具体细节看代码，这里只讨论一下圆心角的求法：

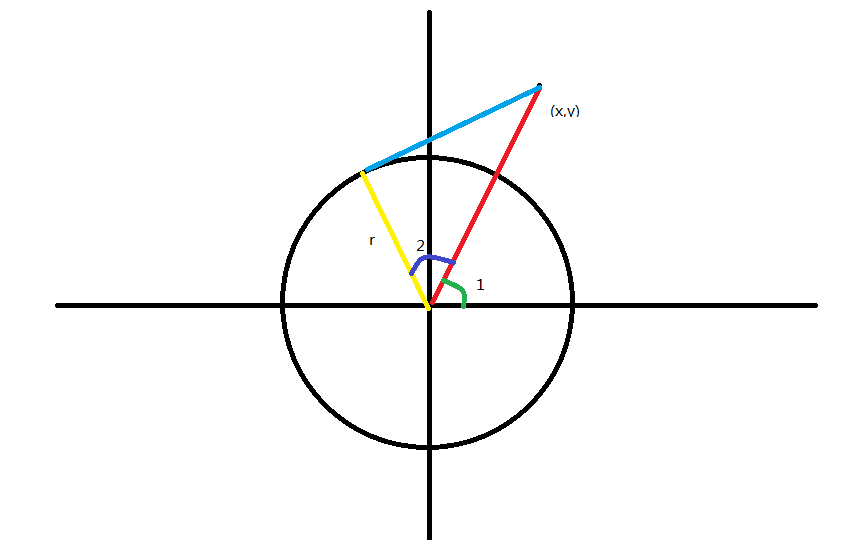
我相信看完这张图你就会求了

具体地，圆心角由两部分组成，一部分是∠1，他等于$arctan(\frac{y}{x})$，另一部分为∠2，他等于$arccos(\frac{r}{\sqrt{x^{2}+y^{2}}})$

然后映射到区间上具体看代码，注意保证取值范围在[-π,π]

于是我们就得到了数轴上很多区间，我们要做的就是找出最多个互相相交不包含的区间

首先按照左端点排序，然后枚举每个左端点作为最左侧的端点，那么满足条件的区间一定在这个左端点对应的右端点左侧，而右端点则在这个右端点的右侧。

然后对于这些右端点，很显然必须是单调递增的，即若$l_{i}<l_{j}$，则一定有$r_{i}<r_{j}$，否则就会出现包含的情况了。

代码：

#include <cstdio>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
const double pi=acos(-1.0);
const double eps=1e-8;
struct Seg
{
    double l,r;
    friend bool operator < (Seg a,Seg b)
    {
        return fabs(a.l-b.l)<eps?a.r<b.r:a.l<b.l;
    }
}s[2005];
double x[2005],y[2005];
double ori[2005];
int my_stack[2005],st[2005],ttop;
int n;
double r;
double get_len(int p)
{
    return sqrt(x[p]*x[p]+y[p]*y[p]);
}
double get_ang(int p)
{
    return atan2(y[p],x[p]);
}
int findf(double x,int lq,int rq)
{
    int ans=rq;
    while(lq<=rq)
    {
        int mid=(lq+rq)>>1;
        if(s[st[mid]].r>x)ans=mid,rq=mid-1;
        else lq=mid+1;
    }
    return ans;
}
int LIS(int t)
{
    ttop=0;
    st[++ttop]=my_stack[1];
    for(int i=2;i<=t;i++)
    {
        if(s[my_stack[i]].r>s[st[ttop]].r)st[++ttop]=my_stack[i];
        else st[findf(s[my_stack[i]].r,1,ttop)]=my_stack[i];
    }
    return ttop;
}
int main()
{
//    freopen("crazy.in","r",stdin);
//    freopen("crazy.out","w",stdout);
    scanf("%d%lf",&n,&r);
    for(int i=1;i<=n;i++)scanf("%lf%lf",&x[i],&y[i]),ori[i]=get_ang(i);
    for(int i=1;i<=n;i++)
    {
        double delt=acos(r/get_len(i));
        double lq=ori[i]-delt,rq=ori[i]+delt;
        if(lq<-pi)lq+=2*pi;
        if(rq>pi)rq-=2*pi;
        if(lq>rq)swap(lq,rq);
        s[i].l=lq,s[i].r=rq;
    }
    sort(s+1,s+n+1);
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        int cnt=0;
        for(int j=i+1;j<=n;j++)if(s[j].l<=s[i].r&&s[j].r>s[i].r)my_stack[++cnt]=j;
        ans=max(ans,LIS(cnt));
    }
    printf("%d\n",ans+1);
    return 0;
}