AT2173

一道乱搞的题...

题意：给你两个字符串，每次操作步骤如下：从前向后扫描整个字符串，对于每一位都有两种选择，一种是保持原来的字符不变，另一种是把这一位上的字符变成和前一位一样（注意是操作后的前一位），问你至少需要多少次操作才能将第一个字符串变成第二个字符串，如果不可能输出-1

题解：

看到网上所有人都在说“画一画就好”，然而我这种蒟蒻根本不会画啊喂！！！

因此这篇博客的目的在于...谈一谈怎么画...

首先我们不难看到：最佳的方法一定是从后向前修改（因为如果从前向后修改，很有可能把要用的字符覆盖掉了，这样就无法成功覆盖了）

接下来，我们维护一个单调递减的变量$posi$，用于记录上一个先前最早匹配的位置在哪

可能这句话并不好理解，我们举个例子讲：

比如原串是$acbaba$，而目标串是$acbacb$，那么合理的对应方式应当是这样的：

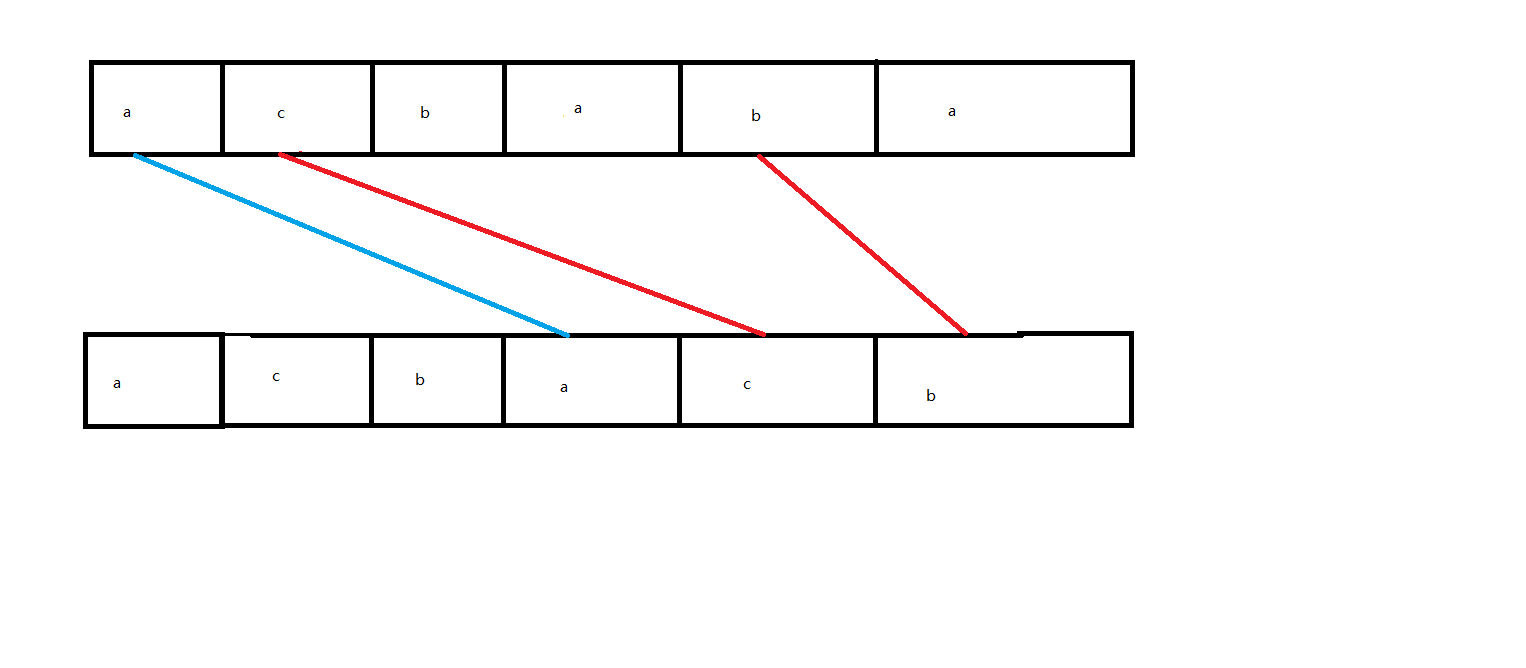
可以看到，虽然4号位置上的$a$之前最近的就是自己上面的$a$，但是不能直接继承，因为5号位上的$c$已经把匹配位置放到2了，为了保证正确覆盖，必须用之前的$a$，这也就导致了前面的无法匹配，所以这是一个无解情况！

那么我们回到有解的情况：

如果有解的话，显然原串中的每一个点最后会覆盖到目标串上的一段区间（废话），那么我们取出这个区间的最左端点来研究即可。

不难发现，每一个值在覆盖的时候一定是一种折线的形式！

举个例子：

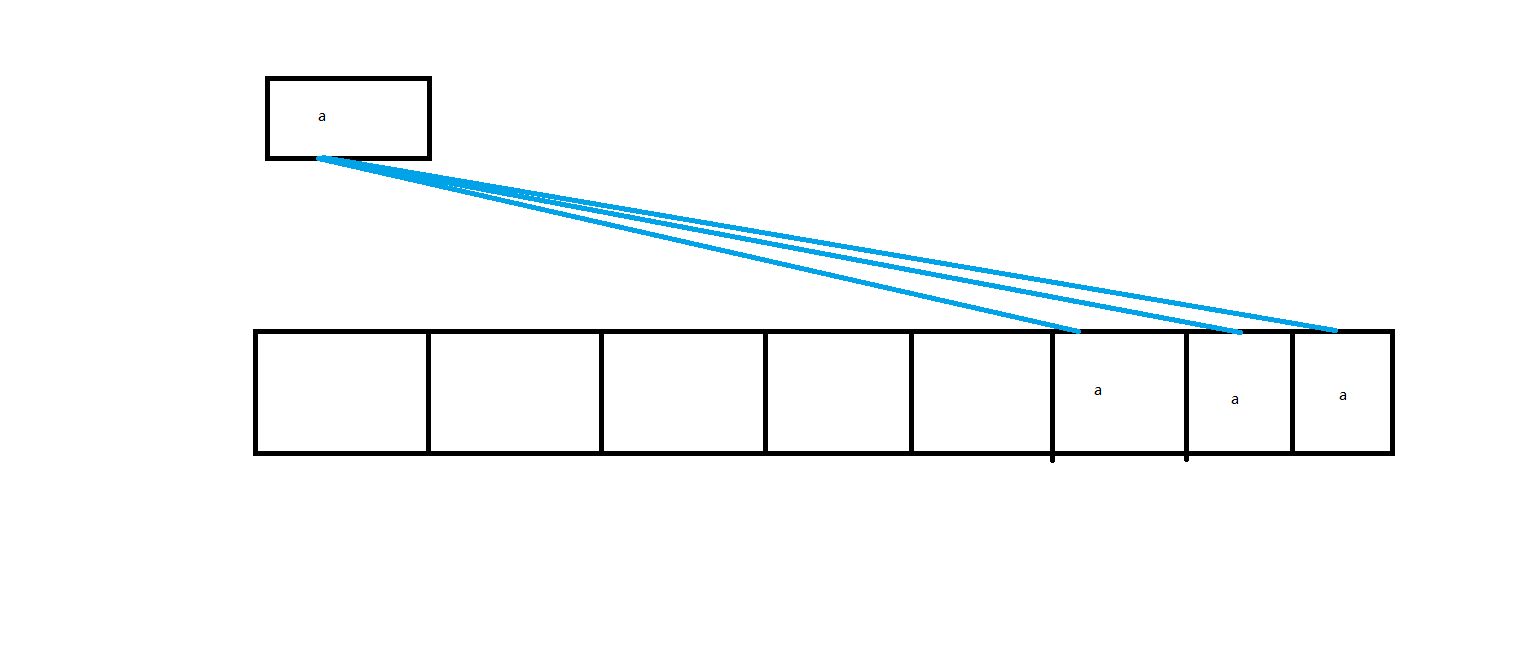
这是一个例子的部分情况

 可以发现：为了覆盖上那三个$a$，我们应该用原来的$a$覆盖整个区间

但是为了避免中间的位置被错误覆盖导致这之后的位置被覆盖，所以我们应该用中间的位置覆盖再去覆盖后面的位置！

举个例子：

$s="abcde",t="aaacc"$

为了防止a开始覆盖后覆盖掉了c导致后面无法被覆盖，我们要先用c去覆盖

所以针对a而言，它的覆盖过程更应该是一条折线！

或者，应该是这样：

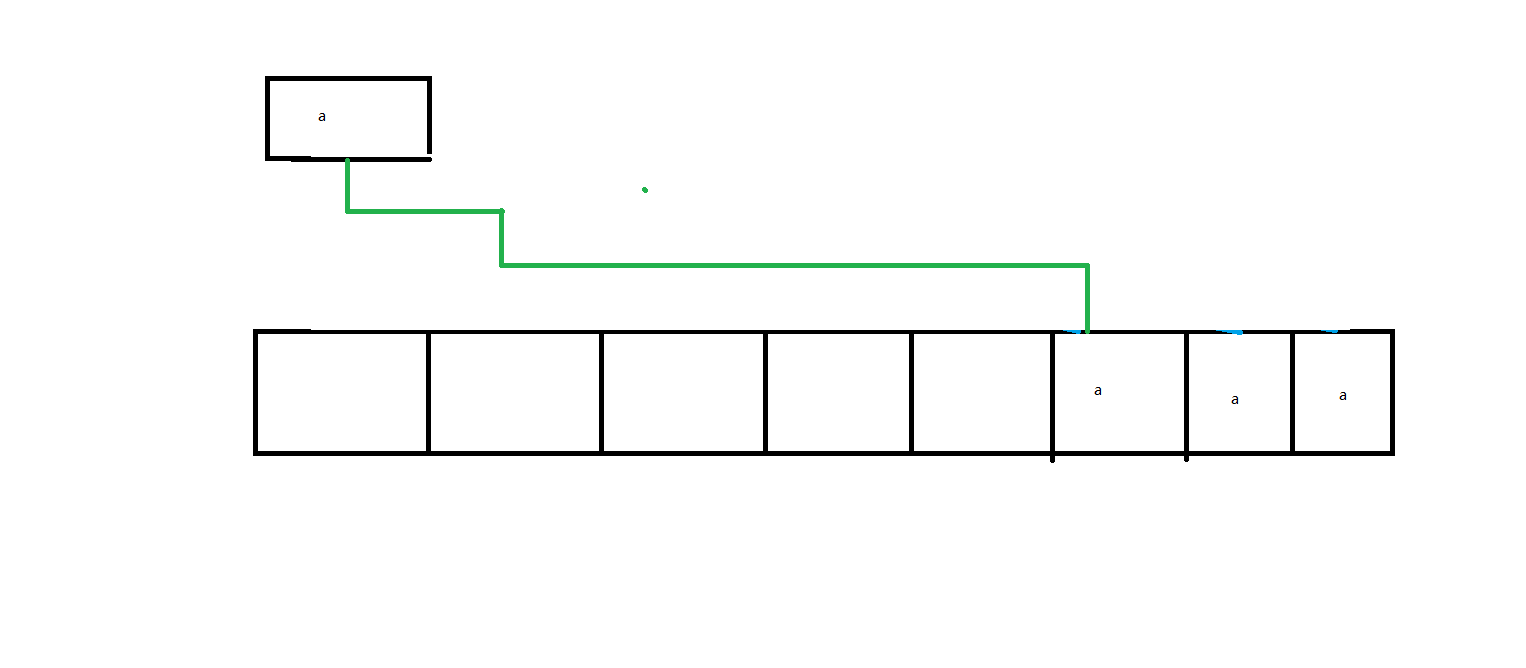
每次向前拓展了一个部分，直到能覆盖上目标即可。

因此，我们只需要求出这样的折线最多折了几次就是答案！

怎么求？

我们开一个队列，队列里储存这样的折线中需要折的每个位置（也即一个位置对应一次偏折），那么队列的大小即为偏折的次数

然后每次将无用的位置弹出队列即可。

#include <cstdio>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;
char s[1000005],t[1000005];
queue <int> Q;
int n;
bool check()
{
    for(int i=1;i<=n;i++)if(s[i]!=t[i])return 0;
    return 1;
}
int main()
{
    freopen("game.in","r",stdin);
    freopen("game.out","w",stdout);
    scanf("%d",&n);
    scanf("%s%s",s+1,t+1);
    if(check()){printf("0\n");return 0;}
    int posi=n;
    int ans=0;
    for(int i=n;i>=1;i--)
    {
        if(t[i]==t[i-1])continue;
        posi=min(posi,i);
        while(posi&&t[i]!=s[posi])posi--;
        if(!posi){printf("-1\n");return 0;}
        while(!Q.empty())
        {
            if((int)Q.front()-(int)Q.size()>=i)Q.pop();
            else break;
        }
        Q.push(posi);
        if(i!=posi)ans=max(ans,(int)Q.size());
    }
    printf("%d\n",ans+1);
    return 0;
}