函数与宏定义实验报告
实验项目：函数与宏定义
姓名:张乐 实验时间：2021年5月27日
一、实验目的与要求
1、掌握函数的调用方法和定义规则；
2、掌握在C语言程序中主调函数与被调函数之间数据传递的规则；
3、了解函数的返回值与类型，并将其正确使用；
4、了解局部变量与全局变量的作用域与它们与储存分类的关系，理解变量的存在性和可见性的概念；
5、熟悉练习递归函数的使用；
6、理解宏的概念，掌握定义无参宏和有参宏的方法；
7、理解文件的概念，并掌握其用法；
二、实验内容
1、实验6.3.1.2
问题描述：求N的阶乘。
实验代码：
#include"stdio.h"
#define N 5
long function(int i)
{
static long f=1;
f=f*i;
return f;
}
void main()
{
long product;
int i;
for (i=1;i<=N;i++)
{
product=function(i);
printf("%d的阶乘是%d\n",i,product);
}
}
运行图：
注意:首先要清楚阶乘定义，所谓 n 的阶乘，就是从 1 开始乘以比前一个数大 1 的数，一直乘到 n，用公式表示就是：1×2×3×4×…×(n-2)×(n-1)×n=n!
2、实验6.3.1.4
问题描述：打印出等边三角形的图案。
实验代码：
#include<stdio.h>
void trangle(int n)
{
int i,j;
for(i=0;i<n;i++)
{
for(j=0;j<n-i;j++)
printf(" ");
for(j=0;j<=2*i;j++)
printf("*");
putchar('\n');
}
}
void main()
{
int n;
printf("请输入一个整数：");
scanf("%d",&n);
printf("\n");
trangle(n);
}
运行图：
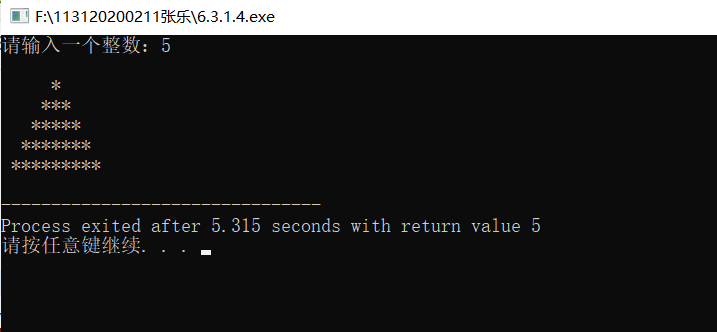
算法思想： （1）设计以高度 n 为参数的一个函数，函数返回值为空，在函数体中实现等腰三角形的打印；图形的最终打印需要利用二层循环设计实现。
（2）图形共输出 n 行，外循环变量 i 表示 n 行的输出，循环变量的变化范围为 0~(n—1)。
（3）循环变量 j 表示每一行的“*”号输出。
（4） 在主函数中输入 n 作为实参，调用定义函数，打印等腰三角形。
3、实验6.3.3.2
问题描述：编写计算学生年龄的递归函数。
实验代码：
#include<stdio.h>
int age(int n)
{
int c;
if(n==1)
c=10;
else
c=age(n-1)+2;
return c;
}
void main()
{
int n=5,sage;
for(n=1;n<=5;n++)
{
sage=age(n);
printf("第%d位学生的年龄为%d\n",n,sage);
}
}
运行图：
算法分析：需要求第5个学生的年龄，age函数就一共被调用几次，最后一次是main函数调用的，其余的是在age函数中调用的。
4、实验6.3.3
问题分析：编写程序，分别从键盘输入数据x和y，计算x的y次幂并输出。
实验代码：
#include"stdio.h"
long getpower(int x,int y)
{
if(y==1)
return x;
else
y=x*getpower(x,y-1);
}
void main()
{
int num,power;
long answer;
printf("输入一个数：");
scanf("%d",&num);
printf("输入幂次方：");
scanf("%d",&power);
answer=getpower(num,power);
printf("%d^%d=%ld\n",num,power,answer);
}
运行图：
