数据结构—平衡二叉树
二叉排序树集中了数组的查找优势以及链表的插入、删除优势,因此在数据结构中占有一定的地位。但在一定的情况下二叉排序树又有可能变为链表,例如插入从1~100的数,这时进行数据查找的效率就要降低。
为了解决二叉排序树这种左右子树深度不均匀的情况引入了一种平衡二叉树(AVLTree):任何一个节点的左右子树深度差不超过1.通过这个限定,阻止了二叉树的左右子树深度差较大的情况,维持了二叉树的稳定。
如何让二叉树的左右子树深度差不超过1呢?这就需要对节点进行旋转,也就是当某个节点的左右子树深度超过1时需要对这个节点进行旋转(旋转之后依旧是左子树小于节点小于右子树),重新调整树的结构。
例如:这两棵二叉树虽然结构不同,但是都是二叉排序树,所谓的旋转就是把左边的深度为3的树旋转为右边深度为2的二叉树。

在平衡二叉树进行插入操作时遇到的不平衡情况有多种,但是这么多种情况都可以分解为一下四中基础情景:把它叫做:左左、左右、右右、右左。
在解释这四种情景之前需要先明白一个定义:最小不平衡节点—插入一个节点之后,距离这个插入节点最近的不平衡节点就是最小不平衡节点(如上图左树的10节点)。所有的旋转都是在最小不平衡节点的基础上进行的。
继续解释四种情景命名意义:左左:节点插入在最小不平衡节点的左子树的左子树上。 左右:节点插入在最小不平衡节点的左子树的右子树上面
右:节点插入在最小不平衡树的右子树的右子树上面。 右左:节点插入在最小不平衡树的右子树的左子树上面。
下面就具体分析这四种情况:
左左:右旋

左左简单不用详解。
左右:先左旋再右旋
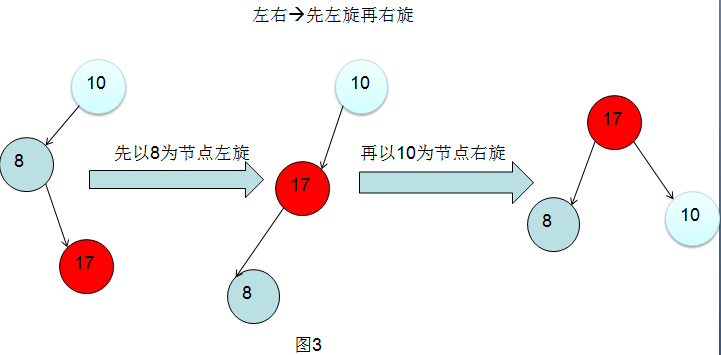
这里有人又有疑问了,上面的左左(图2)看明白了,可这里左右情景为什么要旋转两次呢?为什么先左旋,再右旋呢?
先别急,看看这种情况:(图4)

毫无疑问这也是 左右 情景(左左情景有很多种,图3演示的是最基础的情景,所有 的左左情景的旋转情况和图3都是一样的),那么该怎么旋转呢?

直接右旋不对吧?因为6节点的右子树(以根节点10为中心,靠近内部的子树)6-8经过旋转之后要充当10节点的左子树,这样会导致依旧不平衡。所以在这种左右情景下需要进行两次旋转,先把6的右子树降低高度,然后在进行右旋。即:

把图7 情景和图3的情景一样,这就是为什么 左右情景 需要先左旋再右旋的原因。
在这里可以记作:最小不平衡节点的左节点的内部(以根节点做对称轴,偏向对称轴的为内部。也就是以7为节点的子树)的子树高度高于外部子树的高度时需要进行两次旋转。
右右:左旋

右右情景直接左旋即可。不在详解
右左:先右旋,再左旋

为什么这样旋转明白了吧?如同左右情景,考虑到图10的 右左情景

这种情景旋转如图11

旋转的四种情景就这些了。需要说明的是,下面这两对情景旋转是一样的。
图12都是右左情景,具体看代码的旋转方法就明白了在第一次右旋的时候进行的操作。private Node<T> rotateSingleRight(Node<T> node);

图13都是左右情景,第一次左旋见:private Node<T> rotateSingleLeft(Node<T> node);

旋转情景弄明白之后就是怎么代码实现了,在实现代码之前需要考虑如何进行树高判断。这里就根据定义来,|左子树树高-右子树树高|<2。如果大于等于2则该节点就不在 平衡,需要进行旋转操作。因此在程序中节点中需要定义一个height属性来存储该节点的树高。
由于平衡二叉树的性质,二叉树的高度不会很高,程序使用递归进行数据插入查找不会造成栈溢出异常,所以程序采用递归操作进行插入查找。
平衡的判定策略是在进行递归回溯的时候依照回溯路径更新节点的树高,然后根据|左子树树高-右子树树高|<2来判定该节点是否失衡,进一步对是够旋转进行判定。
程序中的平衡判定策略比较漂亮,当时就是一直卡在这里无法继续进行,然后参考了 AVL树-自平衡二叉查找树(Java实现) 之后采用这种方法才得以解决。
平衡二叉树的删除操作。
对于平衡二叉树的删除操作,只要明白一点就可以了:
如果该节点没有左右子树(该节点为叶子节点)或者只有其中一个子树则可以直接进行删除
否则需要继续进行判定该节点:如果该节点的外部(内外:以根节点做对称轴,靠近对称轴的子树为内部子树)子树树高低于内部子树树高,则找到该节点内部子树的最值(最值:如果内部子树是该节点的右子树则数值为右子树的最小值;如果内部节点是该节点的左子树则数值为该节点左子树的最大值)进行数值交换,交换之后删除该节点即可。
删除之后进行回溯的时候要更新节点的树高,然后判断节点是否平衡,不平衡进行旋转。这时对旋转次数的判定就不同于插入时的判定。
如图14 删除11节点

这种情景需不需要进行两次旋转?该如何判定?
毫无疑问肯定是要进行一次右旋的,但是在右旋之前是不是要进行一次左旋呢?
这就要根据最小不平衡节点的左节点6进行判定,如果6的左节点树高低于6的右节点树高则需要进行一次左旋,最后进行一次右旋结束。
如果6的左子树树高高于6的右子树树高则不需进行左旋可以直接对10节点进行右旋结束操作。
如图15,这种情况肯定需要进行左旋,至于在左旋之前要不要对13节点进行右旋,相信知道该如何判断了。
根据13节点的左右子树高度来判断,左子树(内部)高于右子树(外部)高度则需要进行左旋,图15这种情景是不需要的。

知道了各种旋转的判定标准,程序中就没有其他什么难点了,下面看一下代码:
package com.zpj.datastructure.avlTree;
/**
* @author PerKins Zhu
* @date:2016年8月30日 下午8:01:03
* @version :1.1
*
*/
// 存储数据类型必须实现Comparable接口,实现比较方法
public class AVLTree<T extends Comparable<T>> {
private Node<T> root;
// 定义节点存储数据
private static class Node<T> {
Node<T> left;// 左孩子
Node<T> right;// 右孩子
T data; // 存储数据
int height; // 树高
public Node(Node<T> left, Node<T> right, T data) {
this.left = left;
this.right = right;
this.data = data;
this.height = 0;
}
}
// 对外公开的方法进行插入
public Node<T> insert(T data) {
return root = insert(data, root);
}
// 私有方法进行递归插入,返回插入节点
private Node<T> insert(T data, Node<T> node) {
// 递归终止条件
if (node == null)
return new Node<T>(null, null, data);
// 比较插入数据和待插入节点的大小
int compareResult = data.compareTo(node.data);
if (compareResult > 0) {// 插入node的右子树
node.right = insert(data, node.right);
// 回调时判断是否平衡
if (getHeight(node.right) - getHeight(node.left) == 2) {// 不平衡进行旋转
// 判断是需要进行两次旋转还是需要进行一次旋转
int compareResult02 = data.compareTo(node.right.data);
if (compareResult02 > 0)// 进行一次左旋(右右)
node = rotateSingleLeft(node);
else
// 进行两次旋转,先右旋,再左旋
node = rotateDoubleLeft(node);
}
} else if (compareResult < 0) {// 插入node的左子树
node.left = insert(data, node.left);
// 回调时进行判断是否平衡
if (getHeight(node.left) - getHeight(node.right) == 2) {// 进行旋转
// 判断是需要进行两次旋转还是需要进行一次旋转
int intcompareResult02 = data.compareTo(node.left.data);
if (intcompareResult02 < 0)// 进行一次左旋(左左)
node = rotateSingleRight(node);
else
// 进行两次旋转,先左旋,再右旋
node = rotateDoubleRight(node);
}
}
// 重新计算该节点的树高
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
return node;
}
// 右右情况--进行左旋
private Node<T> rotateSingleLeft(Node<T> node) {
Node<T> rightNode = node.right;
node.right = rightNode.left;
rightNode.left = node;
// 旋转结束计算树高
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
rightNode.height = Math.max(node.height, getHeight(rightNode.right)) + 1;
return rightNode;
}
// 左左情况--进行右旋
private Node<T> rotateSingleRight(Node<T> node) {
Node<T> leftNode = node.left;
node.left = leftNode.right;
leftNode.right = node;
// 旋转结束计算树高
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
leftNode.height = Math.max(getHeight(leftNode.left), node.height) + 1;
return leftNode;
}
// 右左情况--先右旋再左旋
private Node<T> rotateDoubleLeft(Node<T> node) {
// 先进行右旋
node.right = rotateSingleRight(node.right);
// 再加上左旋
node = rotateSingleLeft(node);
return node;
}
// 左右--先左旋再右旋
private Node<T> rotateDoubleRight(Node<T> node) {
// 先进行左旋
node.left = rotateSingleLeft(node.left);
// 在进行右旋
node = rotateSingleRight(node);
return node;
}
// 计算树高
private int getHeight(Node<T> node) {
return node == null ? -1 : node.height;
}
// public 方法供外部进行删除调用
public Node<T> remove(T data) {
return root = remove(data, root);
}
// 递归进行删除,返回比较节点
private Node<T> remove(T data, Node<T> node) {
if (node == null) {// 不存在此节店,返回null.不需要调整树高
return null;
}
int compareResult = data.compareTo(node.data);
if (compareResult == 0) {// 存在此节点进入
/**
* 找到节点之后进行节点删除操作 判断node是否有子树,如果没有子树或者只有一个子树则直接进行删除
* 如果有两个子树,则需要判断node的平衡系数balance
* 如果balance为0或者1则把node和node的左子树的最大值进行交换 否则把node和右子树的最小值进行交换
* 交换数据之后删除该节点 删除之后判断delete节点的父节点是否平衡,如果不平衡进行节点旋转
* 旋转之后返回delete节点的父节点进行回溯
* */
if (node.left != null && node.right != null) { // 此节点存在左右子树
// 判断node节点的balance,然后进行数据交换删除节点
int balance = getHeight(node.left) - getHeight(node.right);
Node<T> temp = node;// 保存需要进行删除的node节点
if (balance == -1) {
// 与右子树的最小值进行交换
exChangeRightData(node, node.right);
} else {
// 与左子树的最大值进行交换
exChangeLeftData(node, node.left);
}
// 此时已经交换完成并且把节点删除完成,则需要重新计算该节点的树高
temp.height = Math.max(getHeight(temp.left), getHeight(temp.right)) + 1;
// 注意此处,返回的是temp,也就是保存的需要删除的节点,而不是替换的节点
return temp;
} else {
// 把node的子节点返回调用处等于删除了node节点
// 此处隐含了一个node.left ==null && node.right == null 的条件,这时返回null
return node.left != null ? node.left : node.right;
}
} else if (compareResult > 0) {// 没找到需要删除的节点继续递归进行寻找
node.right = remove(data, node.right);
// 删除之后进行树高更新
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
// 如果不平衡则进行右旋调整。
if (getHeight(node.left) - getHeight(node.right) == 2) {// 进行旋转
Node<T> leftSon = node.left;
// 判断是否需要进行两次右旋还是一次右旋
// 判断条件就是比较leftSon节点的左右子节点树高
if (leftSon.left.height > leftSon.right.height) {
// 右旋一次
node = rotateSingleRight(node);
} else {
// 两次旋转,先左旋,后右旋
node = rotateDoubleRight(node);
}
}
return node;
} else if (compareResult < 0) {// 没找到需要删除的节点继续递归进行寻找
node.left = remove(data, node.left);
// 删除之后进行树高更新
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
// 如果不平衡进行左旋操作
if (getHeight(node.left) - getHeight(node.right) == 2) {// 进行旋转
Node<T> rightSon = node.right;
// 判断是否需要进行两次右旋还是一次右旋
// 判断条件就是比较rightSon节点的左右子节点树高
if (rightSon.right.height > rightSon.left.height) {
node = rotateSingleLeft(node);
} else {
// 先右旋再左旋
node = rotateDoubleLeft(node);
}
}
return node;
}
return null;
}
// 递归寻找right节点的最大值
private Node<T> exChangeLeftData(Node<T> node, Node<T> right) {
if (right.right != null) {
right.right = exChangeLeftData(node, right.right);
} else {
// 数据进行替换
node.data = right.data;
// 此处已经把替换节点删除
return right.left;
}
right.height = Math.max(getHeight(right.left), getHeight(right.right)) + 1;
// 回溯判断left是否平衡,如果不平衡则进行左旋操作。
int isbanlance = getHeight(right.left) - getHeight(right.right);
if (isbanlance == 2) {// 进行旋转
Node<T> leftSon = node.left;
// 判断是否需要进行两次右旋还是一次右旋
// 判断条件就是比较leftSon节点的左右子节点树高
if (leftSon.left.height > leftSon.right.height) {
// 右旋一次
return node = rotateSingleRight(node);
} else {
// 两次旋转,先左旋,后右旋
return node = rotateDoubleRight(node);
}
}
return right;
}
// 递归寻找left节点的最小值
private Node<T> exChangeRightData(Node<T> node, Node<T> left) {
if (left.left != null) {
left.left = exChangeRightData(node, left.left);
} else {
node.data = left.data;
// 此处已经把替换节点删除
return left.right;
}
left.height = Math.max(getHeight(left.left), getHeight(left.right)) + 1;
// 回溯判断left是否平衡,如果不平衡则进行左旋操作。
int isbanlance = getHeight(left.left) - getHeight(left.right);
if (isbanlance == -2) {// 进行旋转
Node<T> rightSon = node.right;
// 判断是否需要进行两次右旋还是一次右旋
// 判断条件就是比较rightSon节点的左右子节点树高
if (rightSon.right.height > rightSon.left.height) {
return node = rotateSingleLeft(node);
} else {
// 先右旋再左旋
return node = rotateDoubleLeft(node);
}
}
return left;
}
// ************************中序输出 输出结果有小到大*************************************
public void inorderTraverse() {
inorderTraverseData(root);
}
// 递归中序遍历
private void inorderTraverseData(Node<T> node) {
if (node.left != null) {
inorderTraverseData(node.left);
}
System.out.print(node.data + "、");
if (node.right != null) {
inorderTraverseData(node.right);
}
}
}
这段测试程序可以进行测试:
package com.zpj.datastructure.avlTree;
import org.junit.Test;
/**
* @author PerKins Zhu
* @date:2016年8月30日 下午8:42:15
* @version :1.1
*
*/
public class AVLTreeTest {
@Test
public void test01() {
AVLTree tree = new AVLTree();
int array[] = { 28, 35, 5, 35, 26, 30, 1, 21, 18, 35, 7, 30, 25, 1, 7, };
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + ",");
tree.insert(array[i]);
}
System.out.println();
tree.inorderTraverse();
tree.remove(12);
System.out.println();
tree.inorderTraverse();
}
@Test
public void test02() {
AVLTree tree = new AVLTree();
int temp = 0;
for (int i = 0; i < 15; i++) {
int num = (int) (Math.random() * 40);
System.out.print(num + ",");
tree.insert(num);
temp = num;
}
System.out.println();
tree.inorderTraverse();
tree.remove(temp);// 删除插入的最后一个数据
System.out.println();
tree.inorderTraverse();
}
}




