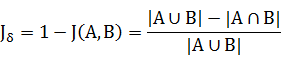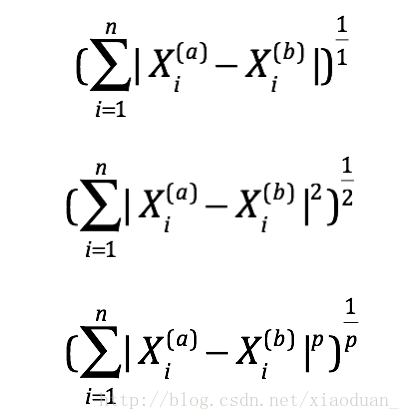网格搜索与K近邻中更多的超参数
网格搜索与K近邻中更多的超参数
网格搜索，Grid Search：一种超参寻优手段；在所有候选的参数选择中，通过循环遍历，尝试每一种可能性，表现最好的参数就是最终的结果。（为什么叫网格搜索？以有两个参数的模型为例，参数a有3种可能，参数b有4种可能，把所有可能性列出来，可以表示成一个3*4的表格，循环过程就像是在每个网格里遍历、搜索，所以叫grid search）
一、knn网格搜索超参寻优
- 首先，准备好数据集。
from sklearn import datasets
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
digits = datasets.load_digits()
x = digits.data
y = digits.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
2. 创建网络搜索的参数：
param_grid = [
{
'weights':['uniform'],
'n_neighbor':[i for i in range(1, 11)]
},
{
'weights':['distance'],
'n_neighbor':[i for i in range(1, 11)],
'p':[i for i in range(1, 6)]
}
]
- 开始对knn的上述超参进行搜索：
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
knn_clf = KNeighborsClassifier()
grid_search = GridSearchCV(knn_clf, param_grid)
%%time
grid_search.fit(x_train, y_train)
输出结果：
Wall time: 2min 20s
GridSearchCV(cv='warn', error_score='raise-deprecating',
estimator=KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform'),
fit_params=None, iid='warn', n_jobs=None,
param_grid=[{'weights': ['uniform'], 'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]}, {'weights': ['distance'], 'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], 'p': [1, 2, 3, 4, 5]}],
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring=None, verbose=0)
grid_search.best_estimator_
grid_search.best_score_
grid_search.best_params_
knn_clf = grid_search.best_estimator_
knn_clf.predict(x_test)
knn_clf.score(x_test, y_test)
其实GridSearch这个类的超参数还有metric_params, metrics等。此外还有一些帮助我们更好理解网格搜索的参数，比如n_jobs表示计算机用多少个核进行。如果为-1表示使用全部的核。比如在搜索的过程中能够显示一些日志信息，verbose，这个值越大输出的值越详细，一般取2就够用了。
%%time
grid_search = GridSearchCV(knn_clf, param_grid, n_jobs=-1, verbose=2)
grid_search.fit(x_train, y_train)
输出结果：
Fitting 3 folds for each of 60 candidates, totalling 180 fits
[Parallel(n_jobs=-1)]: Done 29 tasks | elapsed: 9.5s
[Parallel(n_jobs=-1)]: Done 150 tasks | elapsed: 28.7s
Wall time: 35.5 s
[Parallel(n_jobs=-1)]: Done 180 out of 180 | elapsed: 35.4s finished
二、更多距离的定义
在knn中如果使用distance这个参数，默认使用的是明可夫斯基距离，其中如果p为1，就是曼哈顿距离，p为2，就是欧拉距离。除了这些还有一些距离的定义：
-
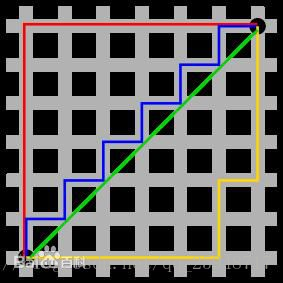
曼哈顿距离
例如在平面上，坐标（x1, y1）的i点与坐标（x2, y2）的j点的曼哈顿距离为：
d(i,j)=|X1-X2|+|Y1-Y2|.
-
欧式距离
-
明可夫斯基距离
可以看做是曼哈顿距离和欧式距离的推广。
在数学中，距离是有严格定义的，需要满足三个性质：非负、对称、三角不等式成立。
1、向量空间余弦相似度
余弦相似度，又称为余弦相似性，是通过计算两个向量的夹角余弦值来评估他们的相似度。
两个向量间的余弦值可以通过使用欧几里得点积公式求出：
余弦距离，就是用1减去这个获得的余弦相似度。余弦距离不满足三角不等式，严格意义上不算是距离。
2、调整余弦相似度
修正cosine相似度的目的是解决cosine相似度仅考虑向量维度方向上的相似而没考虑到各个维度的量纲的差异性，所以在计算相似度的时候，做了每个维度减去均值的修正操作。
比如现在有两个点：（1,2）和（4,5），使用余弦相似度得到的结果是0.98。余弦相似度对数值的不敏感导致了结果的误差，需要修正这种不合理性就出现了调整余弦相似度，即所有维度上的数值都减去一个均值。那么调整后为（-2，-1）和（1,2），再用余弦相似度计算，得到-0.8。
3、皮尔森相关系数
也称皮尔森积矩相关系数(Pearson product-moment correlation coefficient) ，是一种线性相关系数。皮尔森相关系数是用来反映两个变量线性相关程度的统计量。
两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商：
对比协方差公式：皮尔逊相关系数由两部分组成，分子是协方差公式，分母是两个变量的方差乘积。协方差公式有一些缺陷，虽然能反映两个随机变量的相关程度，但其数值上受量纲的影响很大，不能简单地从协方差的数值大小给出变量相关程度的判断。所以，皮尔森相关系数用方差乘积来消除量纲的影响。
4、杰卡德相似系数
-
杰卡德相似系数
两个集合A和B交集元素的个数在A、B并集中所占的比例，称为这两个集合的杰卡德系数。
-
杰卡德距离
杰卡德距离用两个两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。
