递归函数与二分法

递归函数与二分法

• 递归函数

• 二分法

一、递归函数

1.递归定义：

　　在一个函数里再调用这个函数本身就是递归；

　　通俗理解，向下传递需求，需求满足后再将结果回归给上一层；

2.递归表达：

def func():
    pass
    return func()

3.递归的最大深度：

　　理论上来说，递归是无限深的，这样会将内存耗尽，系统有保护机制，定义了递归不能无限的递归，递归层次不能超过1000；一般为997,这个数值看个人电脑情况而定；

#linux系统2G内存测试
>>> def foo(n):
...     print(n)
...     n+=1
...     foo(n)
... 
>>> foo(1)
1
.....
993
994
995
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 4, in foo
  File "<stdin>", line 4, in foo
  File "<stdin>", line 4, in foo
  [Previous line repeated 991 more times]
  File "<stdin>", line 2, in foo
RecursionError: maximum recursion depth exceeded while calling a Python object
996

　　可以通过这种方式来修改递归的最大深度；

#修改最大深度
import sys
print(sys.setrecursionlimit(100000))

　　刚刚我们将python允许的递归深度设置为了10w，至于实际可以达到的深度就取决于计算机的性能了。不过我们还是不推荐修改这个默认的递归深度，因为如果用997层递归都没有解决的问题要么是不适合使用递归来解决要么是你代码写的太烂了～～～

4.看一个小例子：

　　现在你们问我，alex老师多大了？我说我不告诉你，但alex比 egon 大两岁。

　　你想知道alex多大，你是不是还得去问egon？egon说，我也不告诉你，但我比武sir大两岁。

　　你又问武sir，武sir也不告诉你，他说他比金鑫大两岁。

　　那你问金鑫，金鑫告诉你，他40了。。。

　　这个时候你是不是就知道了？alex多大？

1	金鑫	40
2	武sir	42
3	egon	44
4	alex	46

 

 

 

　　你为什么能知道的？

　　首先，你是不是问alex的年龄，结果又找到egon、武sir、金鑫，你挨个儿问过去，一直到拿到一个确切的答案，然后顺着这条线再找回来，才得到最终alex的年龄。这个过程已经非常接近递归的思想。我们就来具体的我分析一下，这几个人之间的规律。

age(4) = age(3) + 2 
age(3) = age(2) + 2
age(2) = age(1) + 2
age(1) = 40

　　那这样的情况下，我们的函数应该怎么写呢？

def age(n):
    if n == 1:
        return 40
    else:
        return age(n-1)+2

print(age(4))

5.使用递归，我们写一个遍历目录的小脚本；

　　要求：用户输入一个路径，然后遍历这个路径下的所有文件；

import os
#导入系统模块

def traverse(filepath,lay):
    d = os.listdir(filepath)
    #获得目录句柄
    for n in d:
    #遍历目录下的文件
        Aap = os.path.join(filepath,n)
        #将扫描到的文件和之前传入的路径进行拼接，形成一个绝对路径，下面用到；
        if os.path.isdir(Aap):
        #判断这个绝对路径是不是目录，是目录继续执行，否则执行else；
            print("\t"*lay,"<"+ n + ">" +":")
            #打印目录名称；
            traverse(Aap,lay+1)
            #继续递归循环进入目录；
        else:
            print("\t"*lay,n)
            #不是目录则打印出当前文件名

traverse("f:/图片/飞",0)

------------------- 输出结果---------------------------------------------
E:\python\venv\Scripts\python3.exe E:/python/s15/递归.py
 <13号地区>:
     13号地区布局图——1.bmp
     13号地区布局图——2.bmp
     13号地区布局图——3.bmp
     13号地区布局图——4.bmp
     nullthumb.jpg
 <寂静村>:
     寂静村——026.bmp
     寂静村——027.bmp
     寂静村——28.bmp
     寂静村——29.bmp
     寂静村——30.bmp
 <死亡中心>:
     12354565.bmp
     死亡中心017.bmp
     死亡中心018.bmp
     死亡中心16.bmp

 

二、二分法：

1.什么是二分查找算法：

　　通俗的说就是：掐头去尾，取中间；

2.二分法的前提：

　　首先要想使用二分法，列表必须是一个有序的列表，比如：[1,2,3,4,5,6,7,8]，不能使杂乱无序的，比如[5,2,9,23,1,234,34,]

3.二分查找法思想：

　　a.拿到一个有序列表后，先用最后一个元素的索引整除2得到中间值n的索引；如: i = (len(li)-1)//2

　　b.拿到中间值索引后，列表通过中间值索引得到中间值n，拿中间值n和要找的数字num进行对比；

　　c.判断，如果中间值n大于要找的数字num，说明要找的数字num在中间值的左边，中间值包含中间值右边的数字可以确认没有我们想要的；

　　　　然后，我们以中间值左一位的元素为最后的元素，获取其索引值；i - 1;

　　e.判断，如果中间值n小于要找的数字num的话，说明要找的数字num在中间值的右边，中间值包含中间值左边的数字可以确认没有我们想要的；

　　　　然后，我们以中间值右一位的元素为左侧的开始元素，获取其索引值i + 1;

　　f.然后我们继续使用二分查找法进行剩余区段查找；知道找到值或者右侧索引值大于左侧索引值该查找结束，如果右侧索引值大于左侧索引值；说明该数字没有在此列表中找到；

4.二分查找法图解：

　　

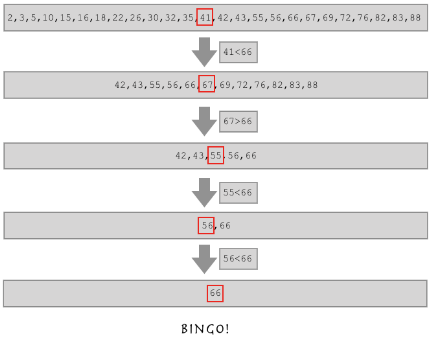
5.二分法实例：

li = [11,22,33,44,55,66,77,88,99,110,158,231,352,443]  #一个有序的列表
num = 77    #要查找的数字
left = 0    #定义左边起始索引
right = len(li)-1   #定义右边结束索引
while left <= right:    #如果左边索引大于等于右边索引，则进行查找，否则该数字不存在
     mid = (left + right)//2    #取中间值索引
     if li[mid] > num:          #根据中间值索引得到中间值并和要查找的数字进行比对
         right = mid - 1        #当中间值大于要查找值时，说明要查找值在中间值右边，此时右边结束索引要定义为中间值索引的左侧索引
     elif li[mid] < num:        #当中间值小于要查找值时，说明要查找值在中间值左边，此时左边起始索引要定义为中间值索引的右侧索引
         left = mid + 1
     else:
         print("找到这个数了，该数字所在索引位置为：%s" % mid)
         break
else:
     print("该数字不存在！")

--------------------- 输出结果-------------------------------------------
找到这个数了，该数字所在索引位置为：6

li = [11,22,33,44,55,66,77,88,99,110,158,231,352,443]
def func(n, left, right):
    if left <= right: # 边界
        mid = (left + right)//2
        if n > li[mid]:
            left = mid + 1
            return func(n, left, right) # 递归  递归的入口
        elif n < li[mid]:
            right = mid - 1
            # 深坑. 函数的返回值返回给调用者
            return func(n, left, right)    # 递归
        elif n == li[mid]:
            print("找到了")
            return mid
            # return  # 通过return返回. 终止递归
    else:
        print("没有这个数") # 递归的出口
        return -1 # 1, 索引+ 2, 什么都不返回, None
# 找70, 左边界:0,  右边界是:len(lst) - 1
ret = func(70, 0, len(li) - 1)
print(ret) # 不是None

---------------- 输出结果 ----------------------------------------
没有这个数
-1

def search(num,l,start=None,end=None):
    start = start if start else 0
    end = end if end is None else len(l) - 1
    mid = (end - start)//2 + start
    if start > end:
        return None
    elif l[mid] > num :
        return search(num,l,start,mid-1)
    elif l[mid] < num:
        return search(num,l,mid+1,end)
    elif l[mid] == num:
        return mid

二分算法终极版