1.1.广义线性模型

下面介绍的是一组用于回归的方法，这些方法的目标值是输入变量的线性组合。用作为预测值。

贯穿模块，我们指定向量为coef_（系数），为intercept_（截距）。

要使用广义线性模型实现分类，详见Logistic回归。

1.1.1.常规最小二乘法

线性回归拟合以系数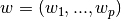最小化可观测到的数据的响应与线性模型预测的响应的残差和的平方，用数学公式表示即：

 

 LinearRegression 对数组X,y使用fit方法，并将结果的系数存放在coef_中：

>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> reg.coef_
array([ 0.5,  0.5])

 

然而，常规最小二乘法系数的估计依赖于模型项的独立（数据点？属性？），当项相关，以及矩阵X的列近似线性相关，矩阵变得近似于相关，这样的结果是，最小而成估计变得对观测值中的随机异常点非常敏感，因此产生巨大的偏差。举例来说，这种多重共线性的情况在实验数据中时常出现。

例子

1.1.1.1.常规最小二乘法的复杂度

这个方法使用对X的单值分解，如果X是(n,p)的矩阵，那么这个方法的消耗是O(np²)，假设n≥p。

1.1.2.岭回归（脊回归）

 岭回归通过对系数施加一个罚项来改善常规最小二乘法的一些问题。岭系数最小化经过罚项优化的平方残差和，数学表达为：

　

这里的α＞0是一个复杂的参数用于控制收缩量：α值越大收缩量越大，因此模型系数对共线性问题更加健壮。（α是一个罚项，值越大对异常点的容忍度越大，因此模型更健壮）。

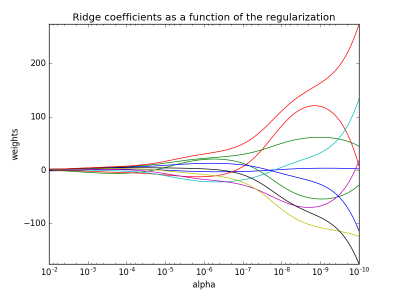
正如其他模型一样，Ridge对数组X和y使用fit方法，并将线性模型的系数存放在coef_中。

>>> from sklearn import linear_model
>>> reg = linear_model.Ridge (alpha = .5)
>>> reg.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1]) 
Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,
      normalize=False, random_state=None, solver='auto', tol=0.001)
>>> reg.coef_
array([ 0.34545455,  0.34545455])
>>> reg.intercept_ 
0.13636...

例子

岭系数作为正则化的函数

使用稀疏特征对文本文档进行分类

1.1.2.1岭复杂度

这个方法的复杂度与常规最小二乘法一样。

1.1.2.2正则花参数设置：通用交叉验证

RidgeCV使用α参数的内置交叉验证实现岭回归。这个对象除了默认设置通用交叉认证（GCV）之外，与GridSearchCV采用同样的工作方式，GCV是留一法交叉验证的有效形式：

>>> from sklearn import linear_model
>>> reg = linear_model.RidgeCV(alphas=[0.1, 1.0, 10.0])
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])       
RidgeCV(alphas=[0.1, 1.0, 10.0], cv=None, fit_intercept=True, scoring=None,
    normalize=False)
>>> reg.alpha_                                      
0.1

参考阅读：“Notes on Regularized Least Squares”, Rifkin & Lippert (technical report, course slides).

1.1.3 Lasso

Lasso 是一个用于估算稀疏系数的线性模型，由于它倾向于用更少的参数值去解决问题，这有效减少了给定解下相互依赖变量的数量，因此它在一些情景下非常好用。因此，Lasso以及它的变种是压缩感知领域的基础。在特定条件下，它可以恢复非零矩阵的精准集（通信技术中的信号复原）。

数学表达下，模型由基于L1prior作为正则化训练的线性模型组成。用于最小化的函数是：

Lasso估计通过增加项来解决最小二乘法罚项，其中α是一个常量，是参数向量的L1norm（范数）。

Lasso类使用坐标下降算法来拟合系数。Least Angle Regression是另外一种算法：

>>> from sklearn import linear_model
>>> reg = linear_model.Lasso(alpha = 0.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=1000,
   normalize=False, positive=False, precompute=False, random_state=None,
   selection='cyclic', tol=0.0001, warm_start=False)
>>> reg.predict([[1, 1]])
array([ 0.8])

对于低阶任务lasso_path函数十分好用，这个函数沿着可能值的全路径计算系数。

例子

• Lasso and Elastic Net for Sparse Signals
• Compressive sensing: tomography reconstruction with L1 prior (Lasso)

 注释：用Lasso进行特征选择

LassoRegression产生稀疏模型，因此可以用它来进行特征选择，详见 L1-based feature selection.

注释：随机稀疏

对于特征选择或稀疏恢复，可使用 Randomized sparse models.

1.1.3.1设置正则化参数

α参数控制稀疏被评估的系数的稀疏阶数。

1.1.3.1.1使用交叉验证