七夕祭
题意
题解
我们将喜欢的店铺称为点。
对于行和列,我们证明一下,如果我们\(i,i+1\)列的点的数量不同,那么一定可以让某一列的点\(--\),另一列的点\(++\)。同时如果现在存在移动是第\(i\)列的一个点移动向了第\(i+1\)列,那么\(i,i+1\)列的点的数量肯定不一样,因为一样的话没有必要移动\(i\)列的过去,而是直接移动\(i+1\)列到达目的地(而且移动了\(i+1\)列一个之后,\(i\)和\(i+1\)列就不一样了,在必要的情况下,第\(i\)列就可以移动向\(i+1\)列了 )。
注:其实这样的证明是证明了下面的情况:
第一行的点的位置:1 3 5
第二行的点的位置:1 3 5
这样如果从第一行移动到第二行不管交换哪两个店铺,都对结果没有影响。
但是我们上面证明了存在其他情况可以比这种情况操作次数更少或者相同,而且我们求的是最少操作次数,所以我们可以忽略这种情况。(当然要注意,在下面的过程中虽然这样交换对结果没有影响,但是下面的算法会默认\(1,1\)或者\(3,3\)交换让第一/二行减少了一个点,另外一行增加了一个点。在存在其他情况操作次数更少的情况下,这种情况会被忽略,但是在相同的时候,我们很有可能会求到这种情况,当然,因为相同,所以无所谓啦,顺便给上一组相同的数据:第一行:1 第二和三行:\(1,2,4,5\) 第四、五行:\(1,4,5\),自己用手推敲一下就知道了。)
那么,上面的证明就证明了我们对于每一行/列而言,在规定最少操作次数的情况下,我们可以把每一行点的个数看成这一行有多少糖果,然后可以移动一颗到左右两行(至于为什么一定可以,上面证明了),然后使每行的点的个数都一样,问最少操作次数,因为每次移动只对行和列其中一个生效,所以可以把行列拆开分别统计,然后列像行一样处理就行了。
当然,其实就是两次糖果传递。
至于答案不存在的情况,很明显就是平均值不是整数的情况了。
作法证法1
核心思想:把所有的变量用一个变量表示出来,将多个变量的极值问题变成一个变量的极值问题。

证明做法2
核心思路:断环+均分纸牌类似思想,同时紧握住全部数加起来等于平均值\(*n\)的性质。
边:\(i\)与\(i+1\)的无向边。走过边的次数即为传递的糖果数。
首先,这个环是可以断开的,但是我们必须要证明存在一条或一条以上的边不走时答案是最优秀的。
- 一条边只可能但方向走动,不可能双方向走动,不然相互抵消
- 根据第一条引理,且最有答案所有的边都走过的话,图可以简化成这样:
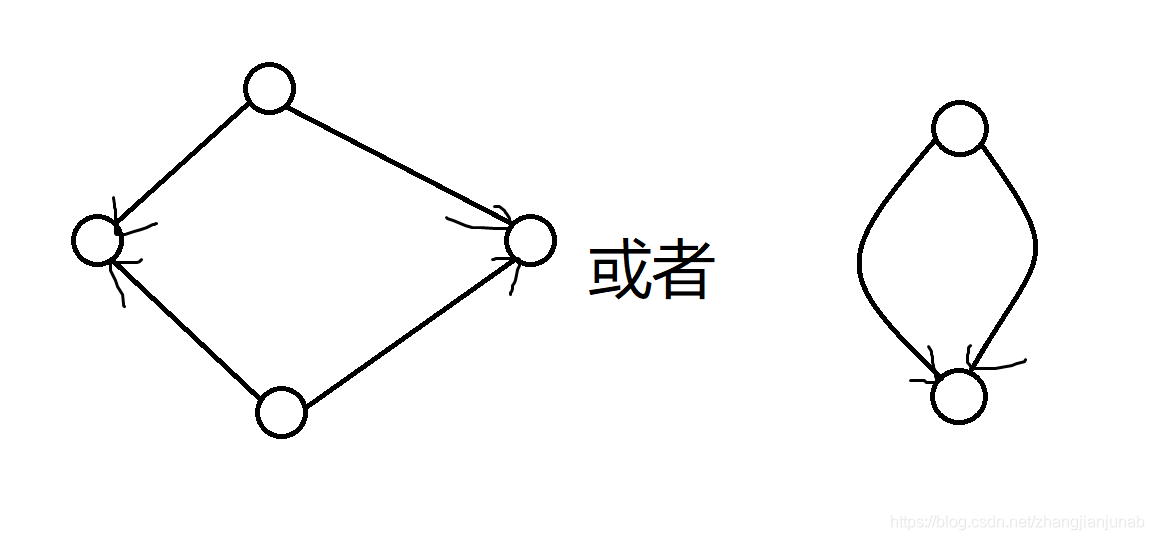
在右边呢,从\(s\)出发有两条路走到\(t\),假设左边的路长小于等于右边,那么右边从\(s\)出发,同时又进入了\(t\),说明肯定有\(s\)的糖果通过右边的路走到了\(t\),那为什么不走左边呢?所以不存在(其实是存在的,但这样同时也存在相同的操作次数但是不是所有边都走过的情况)。
而左边,证法差不多,有两个\(s\)两个\(t\),设上面的是\(s1\),下面的是\(s2\),设上面两条路长,左边减右边是\(x\),下面的左边减右边是\(y\),假设\(x-y≤0\),反之一样证法,那么说明我们让\(s1\)专注于左边的\(t\),而\(s2\)专注于右边的\(t\)这样结果会更优秀或者一样,而专注必然导致一条边不走过,所以也可以证不存在(其实是存在的,但这样同时也存在相同的操作次数但是不是所有边都走过的情况)。
那么我们就可以随便断环进行操作啦。
考虑\(1,2,3,...,n\),其他限制条件一样除了\(1\)可以到\(n\)这个条件。(变成了链。)
平均数是\(ave\)。
这里将一个我认为好理解的讲法,每个点一开始都有些正糖果,但是它可以产生同等数量的正糖果和负糖果,正负糖果相互湮灭,那么对于\(1\)号点而言,他会给\(2\)号点\(a_{1}-ave\)个糖果,正数表示正糖果,而负数表示\(1\)号点自己产生了同等数量的正糖果并将负糖果塞给了二号点,接下来二号点就不能给一号点了,因为一号点已经到了平均值了,它就要去给三号点,这样一直持续下去(不能理解的你也可以这样想,如果二号点需要给一号点一个正糖果,那么就等于一号点给二号点一个负糖果,因此化成了一号点给二号点的单方面运糖果,然后第一步就直接处理完了一号点需要给的糖果,达到了平均值,接下来我们就可以把一号点删掉了,以相同的步骤来操作二号点)。
为了方便,我们把每个位置都减去平均值,这样就是让每个点都到\(0\)就行了。
这样需要的操作步数是:\(a_1+|a_2+a_1|+|a_2+a_1+a_2|+...+|a_n+a_{n-1}+...+a_1|\),那么其实就是每个数字的前缀和。
对于这个这个环状的也是一样,先每个数字减去平均值,我们考虑断开连接第\(k\)到第\(k+1\)个点之间的边,那么设\(s\)为前缀和,答案就是:\(|s[k+1]-s[k]|+|s[k+2]-s[k]|+...+|s[n]-s[k]|+|s[1]+s[n]-s[k]|+|s[2]+s[n]-s[k]|+...+|s[k]+s[n]-s[k]|\),但是\(s[n]\)是\(0\)。
因此我们化成了:\(|s[1]-s[k]|+|s[2]-s[k]|+...+|s[n]-s[k]|\) ,等等,这不就是货仓选址吗?只要\(s[k]\)是中位数就可以让答案最小了,太棒了。
代码
时间复杂度:\(O(nlogn)\)
#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 110000
using namespace std;
typedef long long LL;
LL a[N],b[N],n,m,T,c[N];
inline LL zabs(LL x){return x<0?-x:x;}
LL count(LL *a,LL n)
{
LL res=T/n;
for(LL i=1;i<n;i++)c[i+1]=c[i]+a[i]-res;
sort(c+1,c+n+1);
LL f=c[n/2+1],ans=0;
for(LL i=1;i<=n;i++)ans+=zabs(c[i]-f);
return ans;
}
int main()
{
scanf("%lld%lld%lld",&n,&m,&T);
for(LL i=1;i<=T;i++)
{
LL x,y;scanf("%lld%lld",&x,&y);
a[x]++;b[y]++;
}
if(T%n!=0 && T%m!=0)printf("impossible\n");
else if(T%n!=0)printf("column %lld\n",count(b,m));
else if(T%m!=0)printf("row %lld\n",count(a,n));
else printf("both %lld\n",count(a,n)+count(b,m));
return 0;
}


