关于模拟网络流
参考文献
https://blog.csdn.net/litble/article/details/88410435
https://www.mina.moe/archives/11762
模拟最大流
题意
其实是CF 724 E

这其实是师兄改编了题目QMQ,真实范围应该是\(n<=10000\)
思路
这道题目很明显可以用网络流来做:
但是范围直接T了。
然后我们可以用贪心
然后我们发现这个图貌似有神奇的性质,利用最大流=最小割,我们可以枚举最小割。
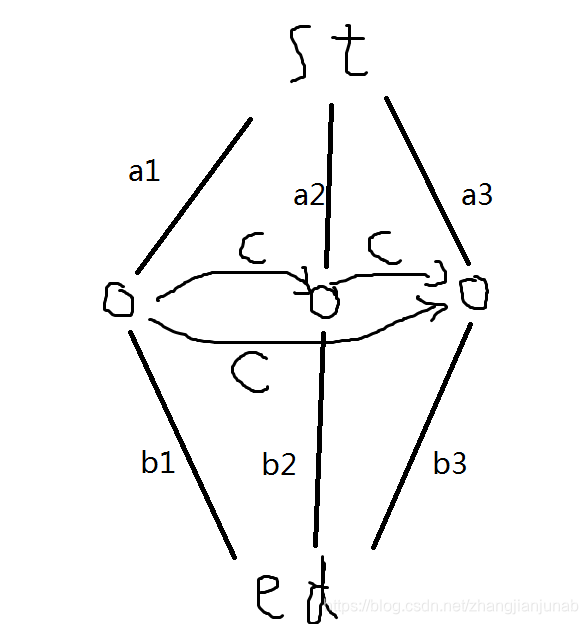
最小割的性质就是每个点要么位于\(st\)集合或者\(ed\)集合,所以我们就可以先枚举出一种情况:
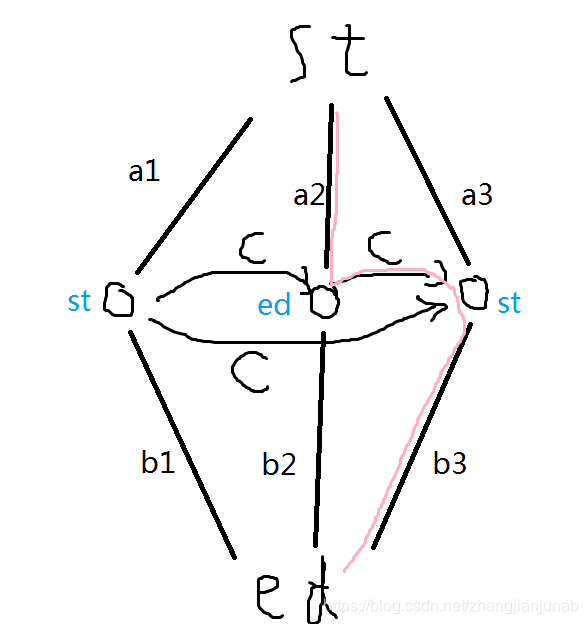
我们发现这个中间的边也要处理,所以对于\(st,ed\)我们还要处理一下,但是我们要如何处理最小割呢?
我们设\(f[i][j]\)表示的是到了第\(i\)个点,有\(j\)个归到\(st\)集合。(归到\(st\)集合就是割掉\(ed\))
那么不计\(C\)的影响的话,不难列出:
\(f[i][j]=min(f[i-1][j-1]+b[i],f[i-1][j]+a[i])\)。
但是如何处理\(C\)呢,不难发现对于\(i,j(i<j)\)如果\(i\)选了\(ed\),\(j\)选了\(st\),那么就会有个\(C\)。
这个该归到\(st\)还是\(ed\)呢,很明显为了DP没有后效性,我们就归到\(ed\)吧。
那么DP转移方程变成了:\(f[i][j]=min(f[i-1][j-1]+b[i],f[i-1][j]+a[i]+j*C)\)。
就可以转移了,时间复杂度\(O(n^2)\),当然,这个又叫模拟网络流。
#include<cstdio>
#include<cstring>
#define N 2100
using namespace std;
typedef long long LL;
inline LL mymin(LL x,LL y){return x<y?x:y;}
LL f[2][N],m;
int a[N],b[N],n;
int main()
{
// freopen("c.in","r",stdin);
// freopen("c.out","w",stdout);
scanf("%d%lld",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)scanf("%d",&b[i]);
int pre=0,now=1;
for(int i=1;i<=n;i++)
{
pre^=now^=pre^=now;
f[now][0]=f[pre][0]+a[i];
for(int j=1;j<i;j++)f[now][j]=mymin(f[pre][j-1]+b[i],f[pre][j]+a[i]+j*m);
f[now][i]=f[pre][i-1]+b[i];
}
LL ans=(LL)9999999999999999;
for(int i=0;i<=n;i++)ans=mymin(ans,f[now][i]);
printf("%lld\n",ans);
return 0;
}
我的思路
我是采用贪心,这道题目\(n\)才\(2000\),还开\(2s\),那么我们不难想到一种贪心思路,就是使得所有卖完粮食后剩余粮食大于\(C\)的位置的粮食尽量的平衡。
也就是尽可能的榨干这个\(C\),使得后面每个位置都可以堆满\(C\)。
至于平衡的值,我们采用二分查找,那么时间复杂度\(O(n^2log值域)\)。
而且还有优化,\(1s\)内过掉。
#include<cstdio>
#include<cstring>
#include<queue>
#define N 3100
using namespace std;
typedef long long LL;
template <class T>
inline T mymin(T x,T y){return x<y?x:y;}
int a[N],b[N];
priority_queue<int>q;//储存粮食信息,当然是大于C的才给放
int sta[N],top;//表示可以移动的粮食
int list[N],tail;
int n,m;
LL zans;
bool check(int x,int k/*原本的数字*/)
{
for(int i=1;i<=top;i++)
{
if(sta[i]<=x)return false;
k+=mymin(sta[i]-x,m);//可以给你多少的数字
if(k>=x)return true;
}
return false;
}
void work(int x,int y)
{
top=0;
while(!q.empty())sta[++top]=q.top(),q.pop();
int k=x-y;//可能是负数
if(top)//有大于C的粮食位置
{
int l=k+1,r=mymin((LL)sta[1],(LL)k+(LL)top*(LL)m),mid,ans=k/*就是不变*/;//表示范围,而且能防止m过小时时间过大
while(l<=r)
{
mid=(l+r)/2;
if(check(mid,k)==true)ans=mid,l=mid+1;
else r=mid-1;
}
for(int i=1;i<=top;i++)
{
if(k==ans)break;
int zjj=mymin(mymin(ans-k,m),sta[i]-ans);sta[i]-=zjj;k+=zjj;
}
}
if(k<0)
{
while(k<0 && tail)k+=list[tail--];
}
zans+=mymin(y,k+y);
if(k>0)
{
if(k<=m)list[++tail]=k;
else q.push(k);
}
for(int i=1;i<=top;i++)
{
if(sta[i]<=m)list[++tail]=sta[i];
else q.push(sta[i]);
}
}
int main()
{
// freopen("c.in","r",stdin);
// freopen("c.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)scanf("%d",&b[i]);
for(int i=1;i<=n;i++)
{
work(a[i],b[i]);
}
printf("%lld\n",zans);
return 0;
}
小结
一般模拟最大流都是模拟最小割。
模拟费用流
普通模版
题意
思路
我们很容易可以想出费用流的构图。
但是这里我们要用贪心加堆模拟费用流。
那么可以发现,这道题目表示的是\(n\)只兔子,有\(m\)个洞,洞有容量,允许左右走,要求每只兔子必须进洞(因为菜的数量和送菜员一样)。
\(x\)为坐标,\(s\)为洞的附加权值。
对于一只兔子\(a\)选了前面的一个洞\(b\),那么产生的费用为\(x_a-x_b+s_b\),而洞的最小值,可以从洞的小根堆直接取。
那么如果后面的一个洞\(c\)抢了\(a\),那么就可以多出\(s_c+x_c-x_a-(x_a-x_b+s_b)=s_c+x_c-2x_a+x_b-s_b\),那么我们只需要添加一个兔子,权值为\(-2x_a+x_b-s_b\),然后我们对于每个洞,都可以取兔子的堆顶,如果贡献\(<0\),那么就可以选了,而如果选了我们构造出来的兔子,就相当于退流,不选洞\(b\)。
当然是不可能有兔子抢\(b\)的,因为这样结果不会是最优的。
但是对于洞\(b\)选了兔子\(a\),那么造成的价值应该是\(v_a+s_b+x_b\)(\(v_a\)为\(a\)在堆中的值),那么如果后面的兔子\(c\)要抢\(b\)的话,那么增加贡献就是\(-v_a-2*x_b\),那么我们需要在洞堆添加这个数字。
你又会问了,那一个兔子的洞被抢了,而洞的兔子又被抢了,不就剩了一对兔子和洞了吗,但是如果你仔细的观察式子就会发现,其实这样子抢的话,这一对的价值是会算上的(其实就是把换的增值去掉了)。
而如果洞\(b\)选了兔子\(a\),而\(c\)洞抢了\(a\)呢?那么很明显设一个兔子权值为\(-s_b-x_b\)就行了,而且这个贪心的正确性在于一个兔子一定进了一个洞,就也就是不管后面怎么抢选他的洞,他都可以回原来的洞。
不过其实如果兔子不一定要求进洞的话,不给他搞洞其实也是可以的,我们考虑为什么可能会错呢?就是我们担心洞找兔子后,添加的洞和兔子的后悔操作同时被触发,但是其实是不会的(而且如果兔子不是必须进洞,你也可以认为兔子进了自己脚下的洞,就是不选)。
因为后面的兔子和洞匹配怕不是更优QMQ。
但是讲了这么多兔子一定要进洞怎么搞,我们只要设无限远的地方有一些洞就行了。
同时多个洞就可以用\(pair\)记录有多少个洞。
而且因为兔子就\(n\)个,所以堆的个数就是\(n\)个,\(O(nlogn)\)。
代码来自https://blog.csdn.net/litble/article/details/88410435。
#include<bits/stdc++.h>
using namespace std;
#define RI register int
int read() {
int q=0;char ch=' ';
while(ch<'0'||ch>'9') ch=getchar();
while(ch>='0'&&ch<='9') q=q*10+ch-'0',ch=getchar();
return q;
}
typedef long long LL;
typedef pair<LL,LL> PR;
const LL inf=1e15;
const int N=100005;
int n,m;LL ans,sumc;
struct node{LL x,w,c;}t[N<<1];
bool cmp(node A,node B) {return A.x<B.x;}
priority_queue<PR,vector<PR>,greater<PR> > q1,q2;
void work() {
q1.push((PR){inf,n});
for(RI i=1;i<=n+m;++i) {
if(t[i].w==-1) {
PR kl=q1.top();LL kv=kl.first;q1.pop();
ans+=kv+t[i].x,--kl.second;
if(kl.second) q1.push(kl);
q2.push((PR){-kv-2*t[i].x,1});//后面可以换洞
}
else {
LL num=t[i].c,sumsum=0;
while(num&&(!q2.empty())) {
PR kl=q2.top();LL kv=kl.first;
if(kv+t[i].w+t[i].x>=0) break;
q2.pop();LL sum=min(kl.second,num);
ans+=(kv+t[i].w+t[i].x)*sum,kl.second-=sum,num-=sum;
if(kl.second) q2.push(kl);
sumsum+=sum,q1.push((PR){-kv-2*t[i].x,sum});//换兔子
}
if(sumsum) q2.push((PR){-t[i].x-t[i].w,sumsum});//换洞
if(num) q1.push((PR){t[i].w-t[i].x,num});
}
}
}
int main()
{
n=read(),m=read();
for(RI i=1;i<=n;++i) t[i].x=read(),t[i].w=-1,t[i].c=0;
for(RI i=1;i<=m;++i)
t[i+n].x=read(),t[i+n].w=read(),t[i+n].c=read(),sumc+=t[i+n].c;
if(sumc<(LL)n) {puts("-1");return 0;}
sort(t+1,t+1+n+m,cmp),work();
printf("%lld\n",ans);
return 0;
}
树上模拟
这道题目的话,我们需要思考一个事情,就是坐标到底要怎么搞?
那么我们可以给每个点设\(dis_x\),表示第\(x\)个点到根的长度。
那么坐标就不是:\(dis_x-dis_y\),而是\(dis_x+dis_y-2*dis_{lca(x,y)}\)了。
所以我们考虑在树上从下往上搞。
堆用左偏树。
对于\(x\),他找到子树\(y\),那么他就可以把自己目前的子树和他对比,即两方的兔子和洞合并,由于贪心局部最优,所以这个子树内的后悔操作已经处理好了。
而两方的兔子洞合并,肯定是各取堆顶是最好的啦,而且有个很显然的事情,就是对于后悔出来的洞和堆,后悔后的兔子和洞肯定也是一个\(x\)一个\(y\),不然从贪心策略讲,\(d\)变小了,所以减的值变小,那么如果是来自同个集合(\(x\)或\(y\))的配对,肯定会比原来更大,那么就肯定不会出现这种情况,所以我们只需要对于\(x\)的兔子,直接合并\(y\)的洞,反之也是。
而且\(lca\)肯定是\(x\),所以先对于\(x,y\)处理一下洞和兔子,然后再合并,找下一棵子树就行了。
不过这里是洞要求必须进,怎么办,那么我们就把他的权值减上一个\(-inf\),要求最优的就一定要进洞吗,然后结果把\(-inf\)去掉。
你好不好奇为什么这里兔子可以直接添加成一个点,你可以认为是他们进了脚下的洞。
而且对于树上。
rtX[x]=merge(rtX[x],newnode(-v2+2*d,sum));
rtY[y]=merge(rtY[y],newnode(-v1+2*d,sum));
这两句话也是一定不会同时触发的,为什么?
因为如果有一个洞和一个兔子分别和这两个洞和兔子配对,那么一定都经过了\(x\),重复,那还不如那两个匹配,这两个原本的匹配在一起(即使最坏也是和原情况相等)。
那么关键是相等怎么判断呢?
设\(x,y\)配对后,\(a\)抢\(x\),\(b\)抢\(y\)
我们不难发现,相等的情况有两个:
- \(a\)为\(lca(x,y)\)的祖先,\(b\)为\(lca(x,y)\)子树内的节点。
- \(a,b\)都为子树内的节点。
那么我们就看\(b\),\(b\)抢了\(y\)后,在\(a\)选时,相当于问你,是\((x,y),(a,b)\)这样更优,还是\((b,y),(a,x)-dis_x+2d\),而\(2d>-dis_x+2d>0\),所以贪心会自动选择\((x,y),(a,b)\),所以我们不用担心。
代码来自https://blog.csdn.net/litble/article/details/88410435
#include<bits/stdc++.h>
using namespace std;
#define RI register int
int read() {
int q=0;char ch=' ';
while(ch<'0'||ch>'9') ch=getchar();
while(ch>='0'&&ch<='9') q=q*10+ch-'0',ch=getchar();
return q;
}
typedef long long LL;
typedef pair<LL,int> PR;
const int N=250005;
const LL inf=1e12;
int n,tot,SZ;LL ans;
int h[N],ne[N<<1],to[N<<1],X[N],Y[N],rtX[N],rtY[N];LL dis[N],w[N<<1];
struct node{int ls,rs,d;PR v;}tr[N*30];
//申请超大结构体要花很多时间,建议拆成单个数组。
int merge(int a,int b) {
if(!a||!b) return a|b;
if(tr[a].v>tr[b].v) swap(a,b);
tr[a].rs=merge(tr[a].rs,b);
if(tr[tr[a].rs].d>tr[tr[a].ls].d) swap(tr[a].ls,tr[a].rs);
tr[a].d=tr[tr[a].rs].d+1;return a;
}
int newnode(LL val,int sum)
{++SZ,tr[SZ].v=(PR){val,sum},tr[SZ].d=1;return SZ;}
void add(int x,int y,LL z) {to[++tot]=y,ne[tot]=h[x],h[x]=tot,w[tot]=z;}
void mer(int x,int y,LL d) {
while(rtX[x]&&rtY[y]) {
LL v1=tr[rtX[x]].v.first,v2=tr[rtY[y]].v.first;
if(v1+v2-2*d>=0) break;
int sum=min(tr[rtX[x]].v.second,tr[rtY[y]].v.second);
ans+=(v1+v2-2*d)*sum;
tr[rtX[x]].v.second-=sum,tr[rtY[y]].v.second-=sum;
if(!tr[rtX[x]].v.second) rtX[x]=merge(tr[rtX[x]].ls,tr[rtX[x]].rs);
if(!tr[rtY[y]].v.second) rtY[y]=merge(tr[rtY[y]].ls,tr[rtY[y]].rs);
rtX[x]=merge(rtX[x],newnode(-v2+2*d,sum));
rtY[y]=merge(rtY[y],newnode(-v1+2*d,sum));
}
}
void dfs(int x,int las) {
if(X[x]) rtX[x]=newnode(dis[x],X[x]);
if(Y[x]) rtY[x]=newnode(dis[x]-inf,Y[x]),ans+=1LL*Y[x]*inf;
for(RI i=h[x];i;i=ne[i]) {
int y=to[i];if(y==las) continue;
dis[y]=dis[x]+w[i],dfs(y,x);
mer(x,y,dis[x]),mer(y,x,dis[x]);
rtX[x]=merge(rtX[x],rtX[y]),rtY[x]=merge(rtY[x],rtY[y]);
}
}
int main()
{
int x,y,z;
n=read();
for(RI i=1;i<n;++i)
x=read(),y=read(),z=read(),add(x,y,z),add(y,x,z);
for(RI i=1;i<=n;++i) {
X[i]=read(),Y[i]=read();
int kl=min(X[i],Y[i]);
X[i]-=kl,Y[i]-=kl;
}
dfs(1,0);
printf("%lld\n",ans);
return 0;
}
时间复杂度的证明
非树证明
这里我们设计到了如果对于洞和兔子都有分身,那么复杂度是多少?
我个人认为是\(O(nlogn)\)带一些常数的,分析是基于算法的分析。
对于兔子。
他找到了一个洞,如果他目前的容量小于这个洞的话,那么这个洞被拆成两个部分,然后\(break\),而对于小于等于,则是把这个洞和兔子匹配,然后生成了一个新的洞,表示抢兔子,而抢洞的则是在最后添加。
如果发现权值大于\(0\),则直接拿这些兔子做一个点插入堆。
观察整个过程,貌似对于一个兔子产生的点的个数级是\(O(1)\)的。
而对于洞,也可以这样分析。
所以就是\(O(nlogn)\)。
树上
这里设计到了合并。
就不是一个个合并了。
我们看一下对于兔子和洞的合并,如果从两个堆中取了兔子和动,并且塞了后悔操作回去,这个后悔操作会不会在本次合并中再次被采用呢?
如果其中一个后悔操作是和原堆中的节点\(x\)合并,那么为什么在配对的时候堆顶不是\(x\)。
所以我们只需要考虑为什么不是一个后悔操作对应一个后悔操作(而且肯定不是原来的一对后悔操作,肯定是不同配对的后悔操作):
那么为什么\(a,x\)在配对的时候堆顶会是\(b,y\)呢?这点需要考虑一下QMQ。
所以每次只会匹配兔子和洞堆的大小的\(min\)。
而且,对于每次堆顶合并,最多会生成三个点。(多了一个点)而真正会参与后面操作的则是两个点,所以我们多出来的点就是合并次数。
那么这个\(min\)要怎么搞呢?
对于两个点数为\(x,y(x<=y)\)的集合,那么他们兔子堆和洞堆中的可以操作的点是\(O(n)\)的。
那么就是\(a+b=x,c+d=y\),求\(min(a,c)+min(b,d)\)的最大值。
\(min(a,c)+min(x-a,y-c)\)
当\(a<=c,x-a<=y-c\)时,那么就是\(x\)。
当\(a<=c,x-a>=y-c\)时,那么合并次数\(<=x\)。
当\(a>=c,x-a<=y-c\)时,那么合并次数\(<=x\)。
所以就是\(x\)。
由于集合合并只会记录最小的集合,那么最坏情况就是两个集合大小相等。
那么就是一个完全二叉树的情况。
而这种情况就是多产生了\(nlogn\)个节点,而还要计算左偏树,所以就是\(O(nlog^2n)\)
不知道是不是对的QAQ。
小结
模拟费用流一般是模拟退流操作
而且对于兔子和洞选择的必要性可以添加点,如某些兔子可以不选,那么就添加一个权值为\(0\)的洞,选了这些洞就是不选,而如果必须选,就添加\(inf\),洞必须进,就把权值\(-inf\),都是些小技巧。

