1.引言
1.引言
1.1 机器学习:是什么以及为什么
We are drowning in information and starving for knowledge. ——John Naisbitt.
我们正在进入大数据时代。举例来说,在网络上有近40万亿张网页;每分钟有近100小时时长的视频上传至Youtube;10世纪人的基因组,每一个都有长度达\(3.8×10^9\)的基本基因对,其测序工作已经被不同的实验室完成;沃尔玛每小时完成1M的交易,并且拥有包含超过\(2.5×10^{15}\)字节信息的数据库。
数据的泛滥要求有对数据进行自动分析的方法,这便是机器学习所能解决的问题。我们定义机器学习(Machine Learning)为一系列可以自动挖掘数据中潜在模式的方法,并且利用发现的模式去预测未来的数据,或者在不确定的情况下执行其他的决策(比如计划如何获取更多的数据!)
全书基于如下观点:解决这类问题(探索数据中的模式)的最好方法是使用概率论中的工具。概率论可以应用在任何涉及不确定度的问题上。在机器学习中,不确定度以很多形式出现:在给定历史数据的前提下未来最有可能出现的数据是什么?能够解释某些数据的最好的模型是什么?在机器学习中所使用的概率论相关的方法与统计学领域有密切的关联,但是两者的侧重点和一些术语上存在些许不同。
本书将介绍多种概率模型,它们分别适用于不同类型的数据和任务。我们也会描述各种机器学习算法并且使用这些算法解决一些问题。我们的目的并不是简单的提供一本关于一项特殊技术的工具书,反之,我们希望透过概率模型和概率推理的视角来展示关于这个领域的统一的观点。尽管我们会关注算法的计算效率,但是将这些算法更好地应用在真正大规模数据集上的细节部分最好还是参考其他的书籍。
然而需要注意的是,即使某人拥有一个表面上十分庞大的数据集,但对于某些特定感兴趣的情况,其中有效的数据量可能也是相当小的。事实上,在很多领域中,数据都呈现出一种长尾(long tail)效应,意味着经常发生的那些事件往往是很少的,大部分事件是很少发生的。比如说,我们经常遇到的那些单词往往也就是那么一小部分(比如“the”和“and”),但是大部分单词(比如“pareidolia”)却很少使用。类似的,有些电影和书很有名,但大部分并非如此。章节2.4.7将进一步介绍长尾效应。长尾效应所导致的一个结果是:我们只需要较少的数据就可以预测或者理解大部分行为。本书主要讨论处理这种数据集的技术。
1.1.1 机器学习的分类
机器学习一般分为2大类。在预测(predictive)或者监督(supervised)学习方法中,模型的目的是:在给定标记数据集(标记数据集是指针对每一个样本\(\mathbf{x}\),都赋予一个标签值\(y\))\(\mathcal{D}=\{(\mathbf{x}_i,y_i)\}_{i=1}^N\)的情况下,通过学习得到一个从输入\(\mathbf{x}\)到输出\(y\)的映射。其中\(\mathcal{D}\)被称为训练集(training set),\(N\)为训练集中样本的数目。
从最简单的情况出发,假设训练集中的每一个输入\(\mathbf{x}_i\)是一个\(D\)维向量,向量中的每一个分量分别代表一个人的身高和体重。这些分量被称为特征(features)、属性(attributes)或者协变量(covariates)。然而在通常情况下,输入向量\(\mathbf{x}_i\)可以是一个复杂的结构化对象,比如一张图片,一个句子,一条邮件,一个时间序列,一个分子形状,一个图表等等。
类似的,模型的输出或者响应(response)变量的形式原则上也可以是多样的,但是在大部分方法中,都假设\(y_i\)是一个类别(categorical)或者名义(nominal)变量,变量取值于一个有限的集合\(y_i\in\{1,...,C\}\)(比如男性或者女性类别),或者\(y_i\)是一个属于实数域的标量(比如一个人的收入)。当\(y_i\)是一个类别变量,相应的问题被称为分类(classification)或者模式识别(pattern recognition),当\(y_i\)是一个属于实数域的标量,相应的问题被称为回归(regression)。回归问题的一个变种是有序回归(ordinal regression),这种情况出现在需要输出多个标签且标签之间具备一些自然的顺序,比如分数等级\(A-F\)。
机器学习中的另一类方法被称为描述性(descriptive)或者无监督(unsupervised)学习方法。在这种情况下,模型给定的输入为\(\mathcal{D}=\{\mathbf{x}\}_{i=1}^N\),模型的目标是在数据中找到“感兴趣的模式”。有时也称这种方法为知识发掘(knowledge discovery)。无监督学习是一个不够明确的问题,因为我们并没有被告知发掘什么类型的模式,所以也没有明确的评价标准可以使用(不像监督学习,我们可以将模型的预测值与观察到的真实值作对比)。
在机器学习中还有一类被称为强化学习(reinforcement learning),在某种程度上很少被使用。在随机的奖励或者惩罚信号的情况下,模型可以更好地学习采取什么的行为。(比如说,考虑一个儿童如何学习走路。)不幸的是,强化学习的内容已经超出本书范畴,尽管我们在5.7节讨论了决策论的内容(强化学习的基础)。
1.2 监督学习(Supervised learning)
我们从监督学习开始对机器学习展开探索,它在实际过程中被广泛使用。
1.2.1 分类
本节我们将讨论分类。分类的目的是得到一个从输入\(\mathbf{x}\)到输出\(y\)的映射,其中\(y\in\{1,...,C\}\),\(C\)为类别的数量。如果\(C=2\),则被称为二分类(binary classification)(在这种情况下,我们通常假设\(y\in\{0,1\}\));如果\(C>2\),则被称为多分类(multiclass classification)。如果类别的标签彼此之间互不排斥(比如某人可以被归类为高的和强壮的),我们称它为多标签分类(multi-label classification), 当然更好的方式是将它理解为预测多个相关二元类标签的问题(即所谓的多变量输出模型)。当我们使用术语“分类”时,我们是指输出单个变量的多分类问题,除非我们特别做出说明。
一种关于上述问题的形式化表达是函数近似(function approximation)。假设存在一个未知函数\(f\),使得\(y=f(\mathbf{x})\),我们的目的是在给定一个含标签的训练集上估计函数\(f\)的形式,然后使用得到的函数\(f\)进行预测\(\hat{y}=\hat{f}(\mathbf{x})\)。(我们使用符号 ^ 表示估计量)。模型最终的目的是为了在新的输入下,即对我们还未观察到的输入进行预测(泛化 generalization),因为基于训练集进行预测是一件十分容易的事(我们可以仅仅通过查表的方式找到答案)。
1.2.1.1 例子
举一个分类问题的小例子,考虑如图1.1(a)所示的问题。我们有两类对象,分别对应标签0(no)和1(yes)。输入为彩色的形状,每个输入通过\(D\)个属性或特征进行描述,所有输入的属性可以被存储在一个大小为\(N\times D\)的设计矩阵\(\mathbf{X}\)中,如图1.1(b)所示。输入特征\(\mathbf{x}\)的取值可以是离散的,连续的,或者是两者的组合。除了输入,在训练集中,包含一个标签向量\(\mathbf{y}\)。
在图1.1中,测试样本为一个蓝色的新月,一个黄色的圆环和一个蓝色的箭头。这些样本在训练集中都没有出现过,所以我们需要模型具备泛化能力,从而在新的数据上也能表现良好。一个合理的猜测是蓝色的新月应该属于类1,因为在训练集中所有的蓝色形状都被标记为1。黄色的圆环很难被分类,因为在训练集中有些黄色被标记为1,有些则被标记为0,有些圆被标记为1,有些圆被标记为0。因此很难说黄色的圆环应该属于哪一类。类似的情况在蓝色箭头上一样适用。

1.2.1.2 概率性预测的必要性
为了处理如上文所提及的预测结果比较模糊的情况(比如黄色的圆环属于哪一类),可以利用概率论中的相关知识。我们假设读者已经具备一定的概率论的相关知识。当然,我们也将会在第二章进行相关知识的回顾。
在给定训练集\(\mathcal{D}\)的情况下,输入向量\(\mathbf{x}\)所属的类别\(y\)服从的分布由\(p(y|\mathbf{x},\mathcal{D})\)表示。通常情况下,这个概率分布的取值有\(C\)个(即\(y\)的取值有\(C\)种,在二分类问题中,\(y\)的取值只有两种,此时我们只需要关心\(p(y=1|\mathbf{x},\mathcal{D})\)的取值即可,因为\(p(y=1|\mathbf{x},\mathcal{D})+p(y=0|\mathbf{x},\mathcal{D})=1\)。在我们的符号表达中,我们明确概率分布以测试输入(新的输入)\(\mathbf{x}\)和训练集\(\mathcal{D}\)作为条件,在形式上表现为\(\mathbf{x}\),\(\mathcal{D}\)被放置在符号“|”后面。当然,在上述的概率分布中我们隐藏了概率分布所基于的模型种类,当我们的预测是基于多种模型时,我们会显式地表达出概率分布对模型种类的依赖\(p(y|\mathbf{x},\mathcal{D},M)\),其中\(M\)表示模型的种类。然而,如果模型的种类在上下文中已经很明确,我们在公式中将不再书写。
如果已知上文中所提及的概率分布\(p(y|\mathbf{x},\mathcal{D})\),那么我们总可以使用下式作出最好的预测,并将其作为真实的标签输出:
式中估计量\(\hat{y}\) 是输入\(\mathbf{x}\) 最有可能的类的标签 , 同时也被称为分布\(p(y|\mathbf{x},\mathcal{D})\)的众数(mode)(在一个概率分布中发生频率最高的情况); 上式又被称为最大后验估计(MAP estimate)。 使用最有可能的输出作为最终的选择从直觉上是正确的,我们将在5.7节给出更加正式的证明。
现在回到之前的例子中,假设我们对黄色圆环的标签存在一个估计值\(\hat{y}\),但其概率值\(p(\hat{y}|\mathbf{x},\mathcal{D})\)远小于1。在这种情况下,我们对这个选择并不是很确定,所以相较于给出这个不信任的答案,直接指出“我不知道”可能会更好,这在医疗或者金融等需要规避风险的领域尤其重要。
关于上文中“我不知道”的回答,有一个十分有趣的应用。有一款电视节目秀Jeopardy,在这个节目中,参赛者需要解决各种单词拼图以及回答一些简单的问题,如果回答错误,他们讲失去奖励。2011年,IBM开发了一款名为Watson的计算机系统,该系统打败了该节目的人类冠军。在Watson使用的一系列有趣的技术中,与我们现在讨论的最相关的技术就是:该系统包含一个模块,该模块用于估计系统对该答案的置信程度。只有当置信度足够高时,系统才会选择给出答案。
另一个需要估计不确定度的重要应用就是在线广告。Google有一个系统SmartASS(add selection system),它可以根据你的检索历史以及其他用户和广告的特征来估计你可能点击一个广告的可能性。这个概率被称为点击率(click-through rate,CTR),它可以用来最大化期望收益。我们将介绍一些类似于SmartASS系统的背后的基本原理。
最近的畅销书\(The \ Signal \ and \ the\ Noise\)给出了许多案例,这些案例说明了在进行预测时,使用概率性的方法是多么重要,无论是政治博弈还是天气预报。
1.2.1.3 实际应用
分类可能是在机器学习中最广泛应用的形式,已经被用来解决很多有趣的但在现实生活中很难解决的问题。接下来,我们将给出更多的例子。
文本分类和垃圾邮箱过滤
在文本分类(document classification)问题中,我们的目标是将一个文本分类成\(C\)类中的一种,这里的文本可以是一个网页或者一个邮件信息,从概率的角度分析,即需要计算\(p(y=c|\mathbf{x},\mathcal{D})\)),其中\(\mathbf{x}\)为某个文本的向量化表示。在文本分类问题中,有一类问题被称为垃圾邮件过滤(email spam filtering),在这类问题中,\(y\)的取值可以是1(垃圾邮件)或者0(非垃圾邮件)。
大部分分类器都假设输入向量\(\mathbf{x}\)的大小是固定的。一种将变长文本转化为固定长度的特征向量的方法是词袋法(bag of words)。我们将在3.4.4.1节解释更多的细节,其基本的思想是如果单词在\(j\)文本\(i\)中出现,则\(x_{ij}=1\)。如果我们使用这种表达方式,我们将得到一个大小为“文本数量×单词数量”的二元矩阵(这里的二元是指矩阵中的每一个元素只能取0或者1),图1.2为我们提供了案例。本质上,文本分类问题已经退化为一个在位中寻找细微的模式变化问题。举例来说,我们可能注意到垃圾信息中存在很高的可能包含单词 "buy", "cheap", "viagra" 等等。在练习8.1和8.2中,你将有机会使用各种分类技术进行垃圾过滤问题。

import numpy as np
import scipy.io as scio
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
import pylab
pylab.rcParams['figure.figsize']=(15,10) # 设置图表的大小
# 载入数据集,并查看数据集基本信息
matfilepath='20news_w100.mat'
data=scio.loadmat(matfilepath)
# print(data)
print('data数据类型为:{0},\ndata中包含的键为:{1}'.format(type(data),data.keys()))
print(data['documents'])
# 查看文本的基本信息,X的形状为(100,16242),其中100为单词数量,16242为文本数量
X = data['documents']
print('X的数据类型为:{0},\nX的形状为:{1}'.format(type(X),X.shape))
# 对X进行转置,形成(16242,100)的矩阵
X = X.T # 对X进行转置
print(X.shape,type(X))
# 查看所有文本对应的标签向量y
y = data['newsgroups']
print('所有文本对应的标签向量y类型为:{0},形状为:{1}'.format(type(y),y.shape))
# 查看所有文本中具有的类的数量
classlabels = data['groupnames']
print(type(classlabels),classlabels.shape)
# 对每个文本中的单词数量进行统计
nwords=np.sum(X,1) # 统计每个文档中的单词数量
print(nwords.shape,'\n',nwords[:5],type(nwords)) # 打印前5个数据
# 根据统计的文本单词数量,提取单词数量最多的前1000个文本
word_num_index = np.argsort(-nwords,axis=0) # 获取降序排序后的索引值
print(word_num_index.shape,type(word_num_index))
index_1000 = np.array(word_num_index[:1000]) # 提取前1000个单词的索引值
print(index_1000.shape,type(index_1000))
XX=X[index_1000.flatten()].toarray() #根据提取的1000个索引值,对X进行花式索引
yy=y.T[index_1000.flatten()] #同样对每个文本的标签值进行花式索引
print(type(XX),XX.shape) # 输出查看相关结果的数据类型
print(type(yy),yy.shape)
new_yy=np.sort(yy,axis=0) # 对yy进行升序排列,将不同的类归置到一起
index_of_yy=np.argsort(yy,axis=0) # 获取排序后的索引值
XX=XX[index_of_yy.flatten()] # 根据获得的索引值对XX进行花式索引
print(XX.shape)
yy_unique=np.unique(new_yy) # 获取标签中的不重合类别
print(yy_unique)
ax = plt.gca()
ax.imshow(XX,cmap=plt.cm.gray_r,aspect='auto') # 根据矩阵绘制灰度图
# 绘制划分类别的分界线
for label in yy_unique[:-1]:
label_index = np.where(new_yy.flatten()==label)[-1][-1]
print(label_index)
line1 = [(0, label_index), (XX.shape[1],label_index)]
(line1_xs, line1_ys) = zip(*line1)
ax.add_line(Line2D(line1_xs, line1_ys, linewidth=3, color='red'))
plt.show()
Figure 1.2 20个新闻组数据大小为16242 x 100的子集。 为了清晰起见,我们只显示1000行。 每行都是一个文档(表示为单词袋位矢量),每列都是一个单词。 红线将4个类分开,即(按降序排列)comp、rec、sci、talk(这些是USENET组的标题)。 我们可以看到,有些单词的存在或不存在都表明了班级。
花朵分类
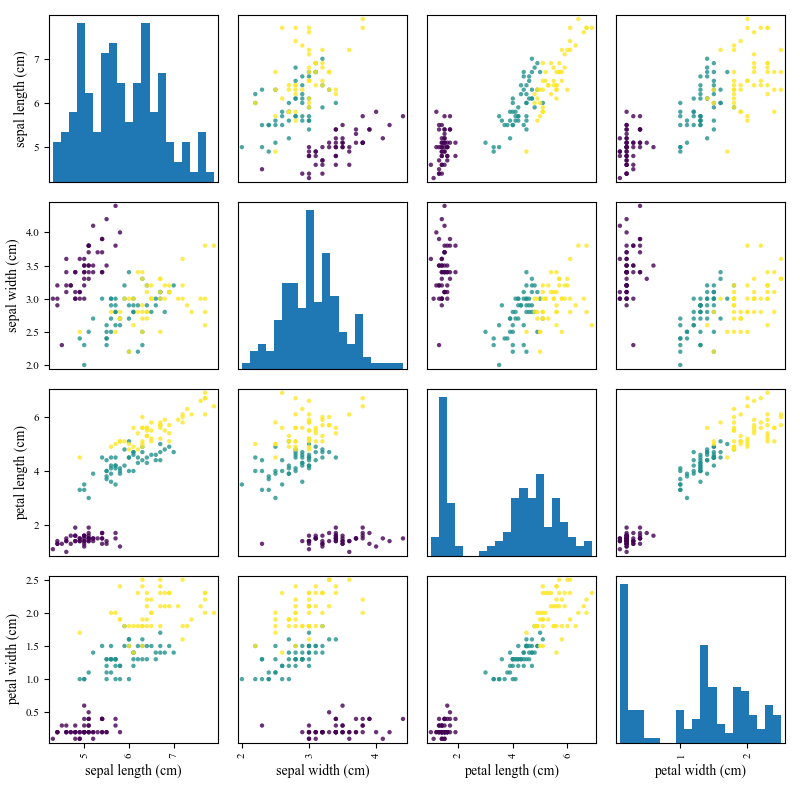
图1.3给出了分类问题的另一个例子,其目的是区分三种不同的鸢尾花,分别为setosa,versicolor和virginica。幸运的是,我们不需要直接对图像进行分类,一个植物学家已经提取了对分类有用的4种特征:萼片长度和宽度,花瓣长度和宽度。类似于这种选择合适特征的工作被称为特征提取(feature extraction),这是一项特别重要而且困难的任务。大部分机器学习方法使用人工选择的特征。后面我们将讨论一些可以从数据中获取好的特征的方法。如果我们如图1.4那样绘制鸢尾花数据的散点图,不难发现,我们仅仅通过花瓣的长度或者宽度就可以将setosas(紫色圆)与其他两种区分开。然而,要想将versiclor与virginica区分开来却有一点难度;任何决定都基于至少2个特征。(在应用机器学习方法之间,对数据进行探索性的分析是十分有用的,比如绘制数据图。)

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
import pandas as pd
iris_dataset = load_iris()
plt.rc('font', family='Times New Roman')
print("鸢尾花数据集的键为:\n{}".format(iris_dataset.keys()))
# 键DESCR为该数据集的描述
print(iris_dataset['DESCR'][:200]+"\n...")
print("鸢尾花的种类:{}".format(iris_dataset['target_names']))
print("鸢尾花的特征:\n{}".format(iris_dataset['feature_names']))
print("鸢尾花数据的类型:{}".format(type(iris_dataset['data'])))
print("鸢尾花的数据形状:{}".format(iris_dataset['data'].shape))
# 查看前5行的数据
print("数据集中前5行的数据:\n{}".format(iris_dataset['data'][:5]))
print("花朵标签的数据类型:{}".format(type(iris_dataset['target'])))
print("花朵标签的数据形状:{}".format(iris_dataset['target'].shape))
print("花朵的标签数据:\n{}".format(iris_dataset['target']))
# 其中0,1,2分别代表类'setosa','versicolor','virginica'
iris_dataframe = pd.DataFrame(iris_dataset['data'],columns=iris_dataset['feature_names'])
grr = pd.plotting.scatter_matrix(iris_dataframe,c=iris_dataset['target'],figsize=(8,8),marker='o',hist_kwds={'bins':20},s=10,alpha=.8)
plt.tight_layout()
plt.savefig('./fisheririsDemo.png')
plt.show()
图像分类和手写识别
下面考虑一个更困难的问题,对图片直接进行分类,这里并不涉及对数据的预处理。我们可能需要对一张图片进行整体上的分类,比如:这张图片是室内还是室外景?它是水平还是垂直的?图中是否包含一条狗?这类任务被称为图像分类(image classification)。
有一种情况比较特殊,即图片中仅包含单独的手写数字和字母,比如一封信的邮政编码,我们可以通过分类实现手写识别(handwriting recognition)。在这个领域中所使用的标准数据集是MNIST,全称为:“Modified National Institute of Standards”(单词“Modified”是指为了使图片中的数字居中而进行了预处理。)这个数据集包含60000张训练图片和10000张测试图片,每张图片上为不同人书写的数字0-9。图片尺寸为28×28,灰度值范围为0:255。图1.5(a)展示了一些样例图。
许多一般的分类方法忽略输入特征中的任意结构,比如空间布局。因此也可以很容易地处理类似于图1.5(b)中的数据,该图中的数据与1.5(a)中的数据是一样的,除了对所有的特征顺序进行了随机打乱。这种灵活性既有优势(因为这些方法是通用的)又有弊端(因为这些方法忽略了一个明显的信息源)。我们将在本书中讨论发掘输入特征的方法。

人脸检测和识别
一个更加困难的问题是在一张图片内发现目标,这被称为目标检测(object detection)或者目标定位(object localization)。一个重要的案例就是人脸检测(face detection)。一种解决这类问题的方法是在不同的位置,以不同的尺度和方向,将图片分割成许多互相重叠的小的区域,然后通过分析这些小的区域中是否存在类人脸的纹理特征来进行分类。这被称为滑动窗口检测器(sliding window detector)。系统将返回那些拥有人脸的概率足够高的位置。图1.6给出了一个例子。这种人脸检测系统内置于大部分的现代数字相机;被检测到的人脸的位置被用来决定自动聚焦的中心。另一个应用是在谷歌街景系统中自动模糊我们的脸。
在找到人脸位置之后,我们可以进行人脸识别(face recognition),也就是估计一个人的身份(见图1.10(a))。在这种情况下,类别的数量可能非常大。同时我们使用的特征与在人脸检测问题中使用的特征不一样:对于人脸识别,脸与脸之间细微的差异,比如发型,可能对决定身份起决定性的作用,但对于检测而言,系统对这些细节信息应该具备不变形(invariant),而应该只是关注脸与非脸之间的区别。

1.2.2 回归
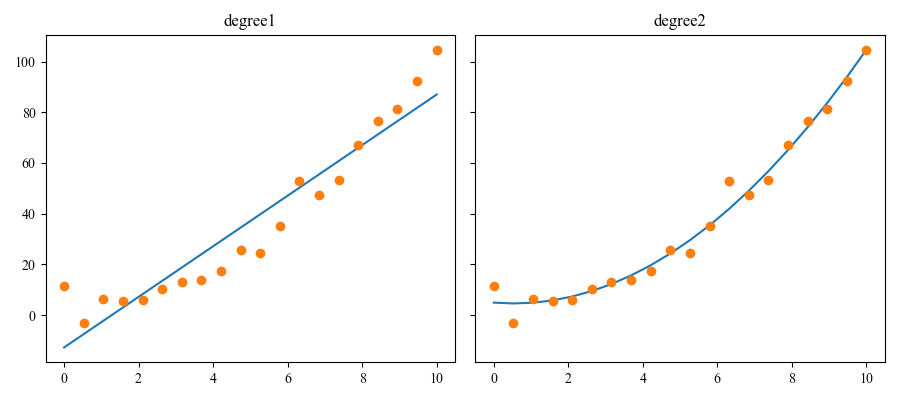
回归与分类很像,不同之处在于,回归所输出的变量是连续的。图1.7展示了一个简单的例子:我们拥有一个实值输入\(x_i\in\mathbb{R}\),和一个相应的输出\(y_i\in\mathbb{R}\)。我们考虑使用两种模式去匹配这些数据:一条直线和一条二次函数曲线(我们将在后文介绍如何训练这些模型)。基于这个基本问题的拓展还有很多,比如高维输入,异常值,非光滑响应等等。我们将在后面介绍处理这些问题的方法。
以下是在现实世界中的一些回归问题。
-
基于当前市场的情况和一些其他的辅助信息预测明天的股票价格;
-
预测一个观看YouTube上特定视频的观众的年龄;
-
给定机器人各电机的控制信号(扭矩),预测机器人手臂末端执行器在三维空间中的位置;
-
根据多种不同临床测量数据预测前列腺特异性抗原(PSA)在体内的数量;
-
使用天气数据,时间等信息预测某建筑内任意位置的温度。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
plt.rc('font',family='Times New Roman')
# 生成x数据
x=np.linspace(0,10,20)
y_net=np.power(x,2)+3 # 生成没有噪音的目标值y_net=x^2+3
noise=4*np.random.randn(20) # 生成服从正态分布的噪音数据,标准差为4,期望为0
y=y_net+noise
print(y.shape,'\n',y[:5]) # 对y值进行噪音上的叠加,并查看部分数据
# 对x进行形状上的改变,sklearn要求样本输入满足(n,d)的形式要求,n为样本数量,d为特征数量
X=x[:,np.newaxis]
# 使用1维特征对数据点进行拟合
lr=LinearRegression().fit(X,y)
XX=np.tile(X,2) # 对X的维度进行拓展,拓展后的X的数据形状为(n,2)
XX[:,1]=np.power(XX[:,1],2) # 第2列数据为x^2
lr2=LinearRegression().fit(XX,y) #使用拓展的特征进行拟合
fig,ax=plt.subplots(1,2,figsize=(9,4),sharey=True)
ax[0].plot(x,lr.predict(X))
ax[0].plot(x,y,'o')
ax[0].set_title('degree1')
ax[1].plot(x,lr2.predict(XX))
ax[1].plot(x,y,'o')
ax[1].set_title('degree2')
plt.tight_layout()
plt.savefig('./linregpolyVsDegree.png')
plt.show()
1.3 非监督学习
我们现在考虑非监督学习,其目标是发现数据中“有趣的结构”;这通常被称为知识挖掘(knowledge discovery)。与监督学习不同,我们并没有被告知每个输入所对应的预期输出。相反,我们将无监督学习任务作为密度估计(density estimation)中的一种, 即我们希望建立一个模型 \(p(\mathbf{x}_i|\mathbf{\theta)}\)。这个形式与监督学习中的概率表达存在两个方面的不同。首先,我们用\(p(\mathbf{x}_i|\mathbf{\theta})\)代替\(p(y_i|\mathbf{x}_i,\mathbf{\theta})\); 即监督学习是一个条件密度估计,然而非监督学习是一个无条件概率估计。第二,\(\mathbf{x}_i\)是一个高维特征向量,所以我们需要建立一个多变量概率模型。相反,在监督学习中,\(y_i\)通常只是一个单独的变量。这就意味着,在大部分监督学习中,我们可以使用单变量概率模型(包含一个与输入相关的参数),从而大大简化了问题本身。 (我们将在第19章讨论多输出分类问题,其中我们将会看到多变量概率模型)
非监督学习可以说是人类和动物学习的典型方法,相较于监督学习,其使用更加广泛,因为它不需要人为的标记数据。含标签的数据不仅很难获得,同时它所具备的信息也相对较少,以至于难以用于估计复杂模型的参数。Geoff Hinton是在ML(机器学习)领域著名的教授,他说:
当我们学习观察事物时,没有人告诉我们正确的答案是什么——我们只是在观察。通常情况下,你的母亲会说“那是一条狗”,但其所具备的信息是很少的。如果你获得一些信息,哪怕一秒钟只有一比特,那也是很幸运的。人类大脑的视觉系统拥有1014个神经连接。一个人的寿命为109秒。所以每秒钟学习一个比特的信息并没有用,你需要额外的105位信息。拥有如此多的信息的地方只有一个,那就是输入本身。——Geoffrey Hinton,1996。
When we’re learning to see, nobody’s telling us what the right answers are — we just look. Every so often, your mother says “that’s a dog”, but that’s very little information. You’d be lucky if you got a few bits of information — even one bit per second — that way. The brain’s visual system has 1014 neural connections. And you only live for 109 seconds. So it’s no use learning one bit per second. You need more like 105 bits per second. And there’s only one place you can get that much information: from the input itself. — Geoffrey Hinton, 1996 (quoted in (Gorder 2006)).
接下来,我们将描述一些在非监督学习中经典的例子。
1.3.1 发现聚类(Discovering clusters)
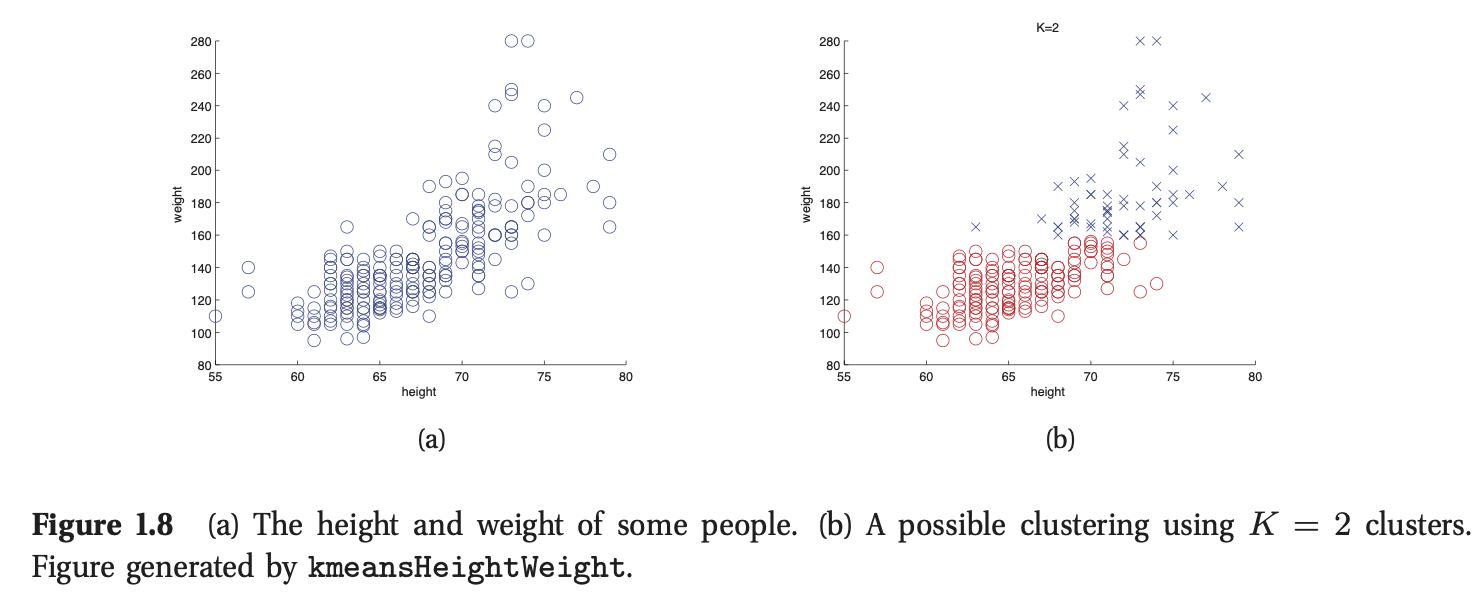
作为非监督学习中的典型案例,考虑将数据聚类为簇(clusters)。举例来说,图1.8(a)绘制了一些2维数据,代表210个人的身高和体重。从图中可以发现,数据中好像存在不同的簇或者子群,尽管我们并不知道这些簇到底有多少个。假设K为簇的数目。我们首先需要估计簇的数目的分布\(p(K|\mathcal{D})\)。为简单起见,我们通常利用\(p(K|\mathcal{D})\)的众数作为估计量,即\(K^*=\arg\max_Kp(K|\mathcal{D})\)。在监督学习中,我们会被告知预测值有多少个类别,但在非监督学习中,我们可以自由选择簇(类)的数目。
我们的第二个目标是估计每个数据点属于哪一个簇。令\(z_i\in\{1,...,K\}\)代表数据点\(i\)所归属的簇。(\(z_i\)又被称为隐变量或者潜变量,因为在训练集中从未见过)。我们可以通过计算\(z_i^*=\arg\max_kp(z_i=k|\mathbf{x_i|\mathcal{D}})\)来推测每个数据点所归属的簇。如图1.8(b)所示,我们使用不同的颜色代表不同的簇,其中我们假设\(K=2\)。
在本书中,我们主要关注基于模型方法的聚类(model based clustering),这就意味着我们利用概率模型去对数据进行拟合,而不是其他的一些算法。基于模型方法的优势在于,我们可以客观的比较不同的模型,并且在一些大规模系统中,我们可以将不同的模型组合起来。
以下是在现实世界中的一些聚类的应用:
-
在天文学中,autoclass系统通过对天体物理测量数据聚类,发现了一种新型恒星。
-
在电子商务中,我们经常会根据客户的购买行为或者网站搜索行为将它们聚类到不同簇中,然后针对不同的簇发送定制的广告。
-
在生物学中,流式细胞术数据通常聚类成组,以发现不同的细胞亚群。
1.3.2 发现潜在因子(Discovering latent factors)
在处理维度特别高的数据时,通常需要通过将数据投影到低维空间中实现数据的降维,从而获得数据的“本质”。一个简单的例子如图1.9所示,其中我们将一些3d数据投影到一个2d平面。这个2d的近似效果很好,因为大部分点都靠近这个子空间。将数据点映射到直线上可以将数据降到1维空间,如图1.9(a)所示;这种近似的效果并不好。
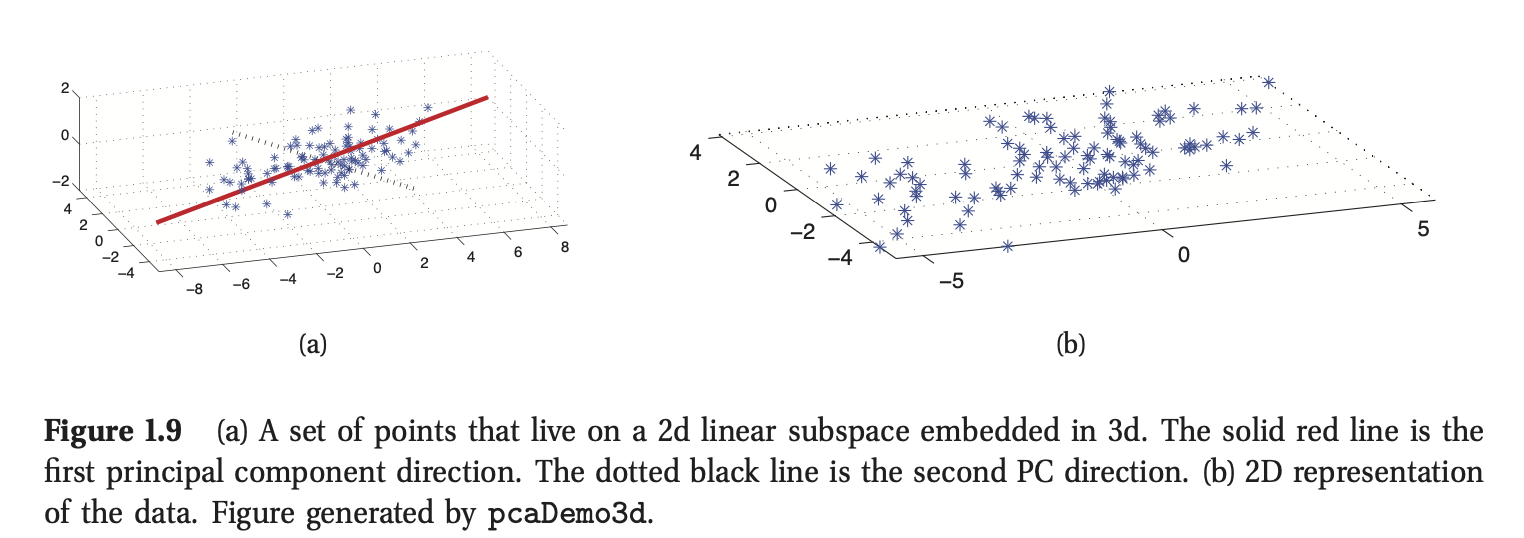
降维背后的动力在于尽管实际的数据可能是高维的,但其可能只有少量的主导因素,这些潜在的主导因素被称为潜在因子(latent factors)。举例来说,当我们对人脸图像进行建模时,可能只有少数潜在的因子主导着不同图像的变化,比如光线,位置,身份(但是一张图像的维度却很高)等等。图1.10给出了示例说明。

将低维的特征向量表示作为统计模型的输入往往会取得更好的预测精度,因为输入仅仅关注了数据的“本质”,排除了那些不必要特征。同时,低维表示可以加快最近邻目标的搜索,数据在二维空间的投影可以使数据的可视化更加直观。
最常用的降维方法是主成分分析(principal components analysis, PCA)。这可以被认为是(多输出)线性回归的非监督版本,在PCA中,我们观察到的是最终的高维响应数据\(\mathbf{y}\),而不是低维的“起因”\(\mathbf{z}\),所以模型具备形式\(\mathbf{z}\rightarrow\mathbf{y}\),我们需要“反转这个箭头”,从观察到的高维数据\(\mathbf{y}\)推断出潜在的低维数据\(\mathbf{z}\)。
降维,尤其是PCA,已经在很多领域中得到应用。
-
在生物学中,通常使用PCA来分析基因微阵列数据,以解释每个测量结果通常是许多基因共同作用的效果,这些基因通过它们属于不同生物途径的事实而在它们的行为中相互关联。
-
在自然语言处理中,通常使用一种称为潜在语义分析的PCA变体进行文档检索(见27.2.2节)。
-
在信号处理(例如声学或神经信号)中,通常使用ICA (PCA的一种变体)将信号分离成不同的源(见第12.6节)。
-
在计算机图形学中,通常将运动捕捉数据投影到低维空间中,并用它来创建动画。有关处理此类问题的一种方法,请参见第15.5节。
1.3.3 发现图结构(Discovering graph structure)
有时我们测量一组相关的变量,我们想要发现哪些变量与哪些变量最相关。这可以用图\(G\)表示,其中节点表示变量,边表示变量之间的直接依赖关系(我们将在第10章讨论图模型时对此进行详细说明)。然后我们可以从数据中学习这个图形结构,即我们计算\(\hat{G}=\arg\max p(G|\mathcal{D})\)).
与一般的无监督学习一样,稀疏图的学习主要有两种应用:发现新知识和获得更好的联合概率密度估计器。现在我们分别给出一些例子。
- 学习稀疏图形模型的大部分动机来自于系统生物学社区。例如,假设我们测量细胞中某些蛋白质的磷酸化状态(Sachs等,2005)。图1.11给出了一个从这些数据中学习到的图结构示例(使用第26.7.2节中讨论的方法)。另一个例子,Smith等人。(2006)表明可以从时序脑电图数据中恢复某一种鸟的神经“接线图”。恢复的结构与已知的鸟类大脑这部分的功能连接紧密吻合。
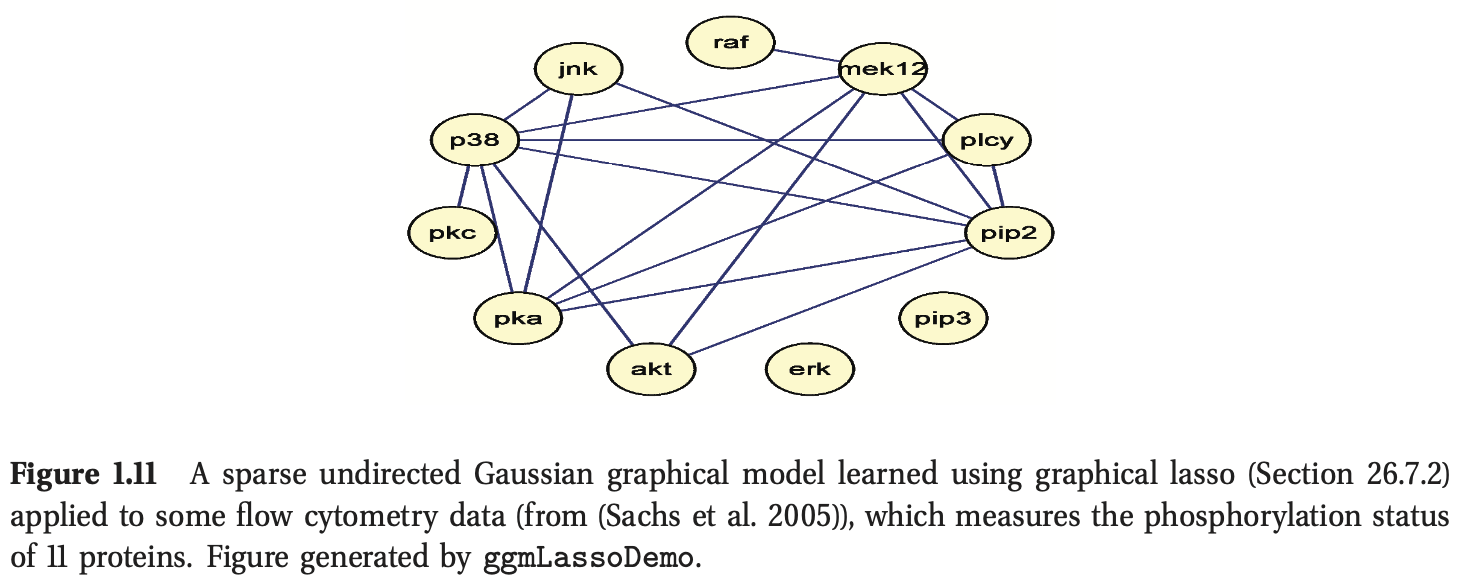
- 在某些情况下,我们对解释图形结构不感兴趣,我们只是想用它来建模相关性和做出预测。这方面的一个例子是在金融投资组合管理中,大量不同股票之间的协方差的准确模型是很重要的。Carvalho and West的研究表明,通过学习稀疏图,然后将其作为交易策略的基础,有可能跑赢大盘。比不利用稀疏图的方法赚更多的钱。另一个例子是预测高速公路上的交通堵塞。Horvitz等人描述了一个名为JamBayes的已部署系统,用于预测西雅图地区的交通流量;预测是使用从数据中学习结构的图形模型做出的。
1.3.4 矩阵补全(Matrix completion)
有时我们会丢失数据,也就是说,变量的值是未知的。例如,我们可能进行了一项调查,而有些人可能没有回答某些问题。或者我们可能有各种各样的传感器,其中一些失灵了。相应的设计矩阵中就会有“孔”;这些缺失的条目通常由NaN表示,NaN代表“不是一个数”。补全(imputation)的目的是推断出缺失项似是而非的值。这有时被称为矩阵补全(matrix completion)。下面我们给出一些示例应用程序。
1.3.2.1 图像修复(Image inpainting)
类似于补全任务的一个有趣的例子是图像修复(image inpainting)。目标是在一个具有真实纹理的图像中“填补”洞(例如,由于划痕或遮挡)。如图1.12所示,在图1.12中,我们对图像进行去噪,并修复遮挡后面隐藏的像素。这可以通过建立像素的联合概率模型来解决,给定一组干净的图像,然后在已知变量下推断未知变量(像素)。这有点像masket basket分析,只是数据是实值和空间结构化的,所以我们使用的概率模型是不同的。有关一些可能的选择,请参阅第19.6.2.7和13.8.4节。

1.3.2.2 协同过滤(Collaborative filtering)
另一个类似补全任务的有趣例子是协同过滤(collaborative filtering)。这方面的一个常见例子是根据某些人和其他人如何评价他们已经看过的电影来预测人们想要观看哪些电影。关键的观点是,预测并不基于电影或用户的特征(尽管有可能),而仅仅是基于评分矩阵。更精确地说,我们有一个矩阵\(\mathbf{X}\),其中\(X(m,u)\)是用户\(u\)对电影\(m\)的排名(假设一个介于1和5之间的整数,其中1表示不喜欢,5表示喜欢)。注意,\(\mathbf{X}\)中的大多数条目将会丢失或未知,因为大多数用户不会对大多数电影进行评级。因此我们只观察到\(\mathbf{X}\)矩阵的一个很小的子集,我们想要预测一个不同的子集。特别是,对于任何给定的用户\(u\),我们可能想要预测他/她最喜欢看哪些未被排名的电影。
为了鼓励这一领域的研究,DVD租赁公司Netflix于2006年发起了一项竞赛,奖金100万美元(见http://netflixprize.com/)。特别是,他们为∼500k用户创建的∼18k影片提供了一个大的评分矩阵,范围从1到5。整个矩阵将有∼9×109个元素,但是只有大约1%的元素被观测到,所以这个矩阵非常稀疏。其中一部分用于训练,其余用于测试,如图1.13所示。这次竞赛的目标是比Netflix现有的系统预测得更准确。2009年9月21日,该奖项被授予了一个名为“BellKor’s Pragmatic Chaos”的研究团队。第27.6.2节讨论了它们的一些方法。有关这些团队及其方法的详细信息,请访问http://www.netflixprize.com/community/viewtopic.php?id=1537。
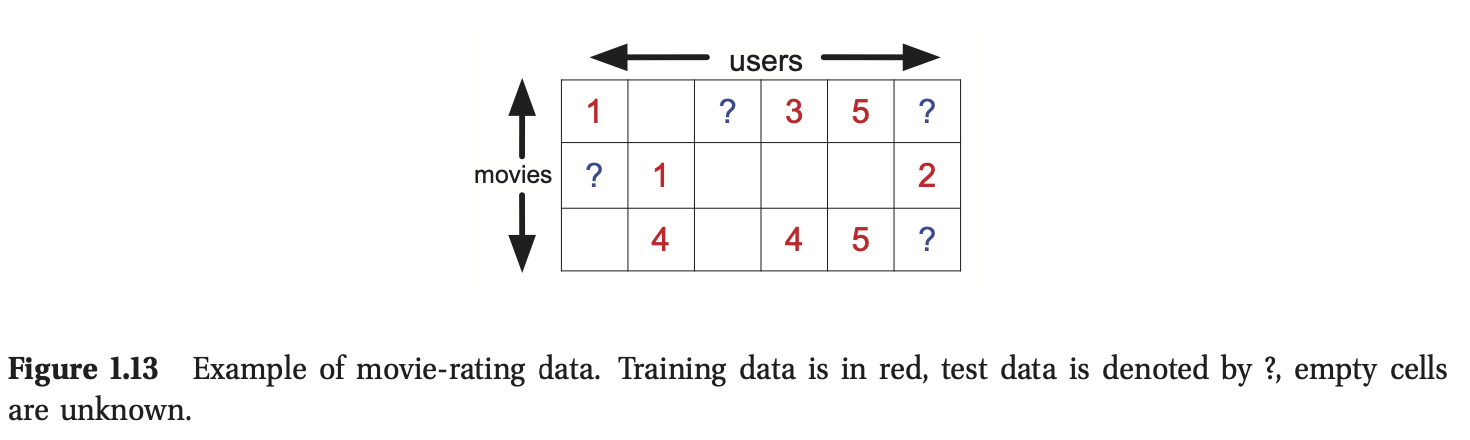
1.3.2.3 购物篮分析(Market basket analysis)
在商业数据挖掘中,人们对一项名为购物篮分析(market basket analysis)的任务非常感兴趣。数据由一个二进制矩阵(通常非常大但稀疏)组成,其中每一列表示一个项目或产品,每一行表示一个交易。如果项目j是在第\(i\)个交易上购买的,则\(x_{ij}=1\)。许多商品都是一起购买的(例如,面包和黄油),所以各个部分之间会有关联。给定一个新的部分观察到的位向量,表示消费者购买的商品的子集,目标是预测这个位向量其他哪些位会被激活,即哪些产品可能会被购买。(与协同过滤不同,我们通常假设训练数据中没有缺失的数据,因为我们知道每个客户过去的购物行为。)
除了建模购买模式之外,此任务还出现在其他领域。例如,可以使用类似的技术对复杂软件系统中的文件之间的依赖关系建模。在这种情况下,任务是给定一个已更改的文件子集,预测哪些其他文件需要更新以确保一致性。
解决这类任务的一般方法是频繁项集挖掘(frequent itemset mining),该方法创建关联规则。另外,我们也可以采用概率方法,针对位向量拟合联合概率密度模型\(p(x_1,...,x_D)\) 。这样的模型通常比关联规则具有更好的预测精度,尽管它们可能不太容易解释。这是数据挖掘和机器学习的典型区别:在数据挖掘中,更强调可解释模型,而在机器学习中,更强调准确的模型。
1.4 机器学习中的一些基本概念
本章,我们将介绍机器学习中一些核心概念。我们将在后面的内容中扩展这些概念。但在此处会进行简单介绍。
1.4.1 参数模型和非参数模型
在本书中,我们将关注概率模型\(p(y|\mathbf{x})\)或\(p(\mathbf{x})\),采用哪种模型取决于研究的问题是监督学习还是非监督学习。有很多方法来确定概率模型,不同方法中最重要的区别在于:模型是否具备固定的参数数量,或者说参数数量是否随训练样本的增加而增加?前者被称为参数模型(parametric model),后者被称为非参数模型(non-parametric model)。参数模型的优势在于使用起来更加快捷,其缺点在于它需要对数据分布作很强的假设。非参数模型则更加灵活,但是对于大的数据集而言,其计算难度通常很大。我们在后面的章节中给出两种模型的例子。为了方便,我们主要针对监督学习进行讨论,尽管我们很多的讨论同样适用于非监督学习。
1.4.2 一个简单的非参数分类器:K近邻(K-nearest neighbors)
非参数分类器的简单例子是K近邻(KNN)分类器。在这个模型中,针对测试输入\(\mathbf{x}\)的分类仅仅参考距离该点最近的K个训练集中的样本,统计在这个集合(K个邻居)中,每个类的数量,返回在这个集合中每个类别的占比作为估计量,图1.14给出了说明,形式上表达为:
其中\(N_K(\mathbf{x},\mathcal{D})\)为在数据集\(\mathcal{D}\)中距离\(\mathbf{x}\)最近的\(K\)个数据点,\(\mathbb{I}\)为指示函数,定义为:
这个方法被称为基于存储的学习(memory-based learning)或者基于样例的学习(instance-based learning)。在这个方法中,最常用的距离测度为欧氏距离(该距离将这个技术限制在了实数领域),尽管其他的测度也可以使用。
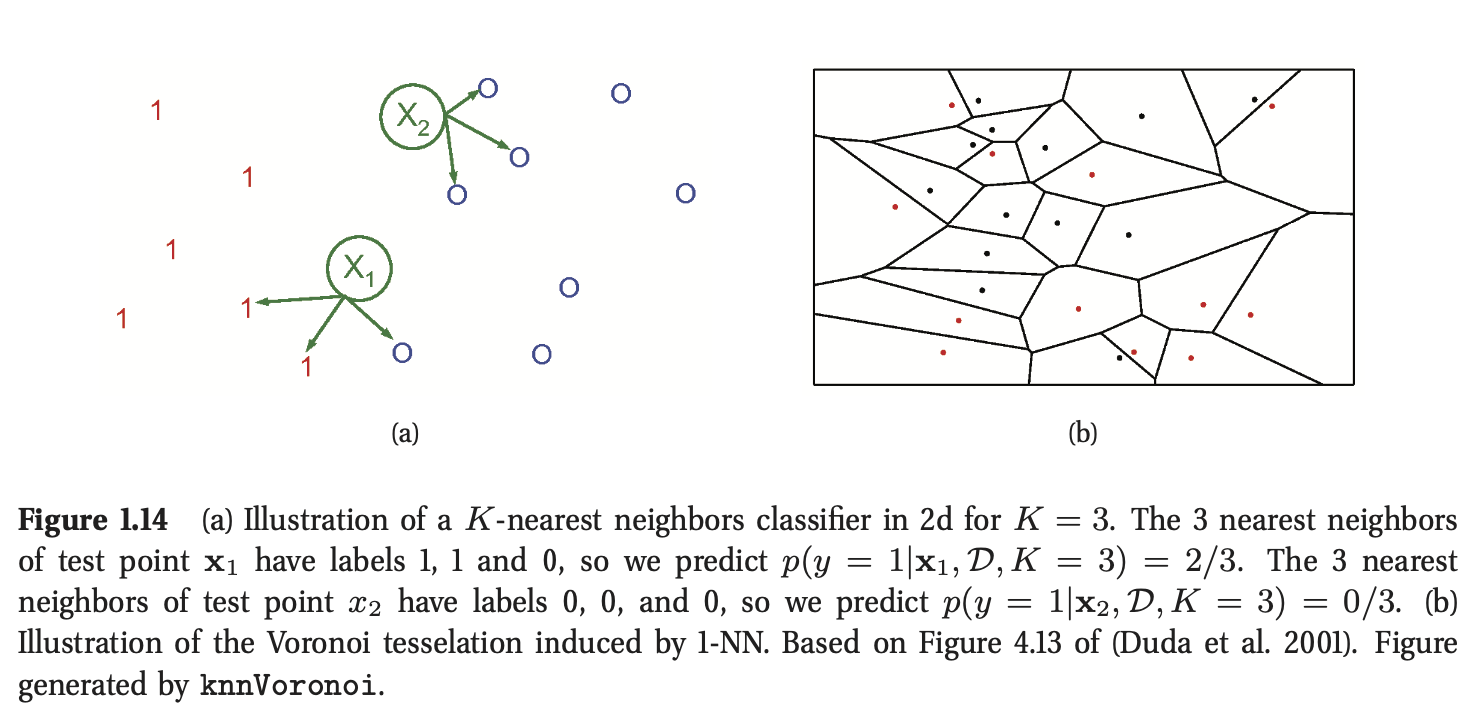
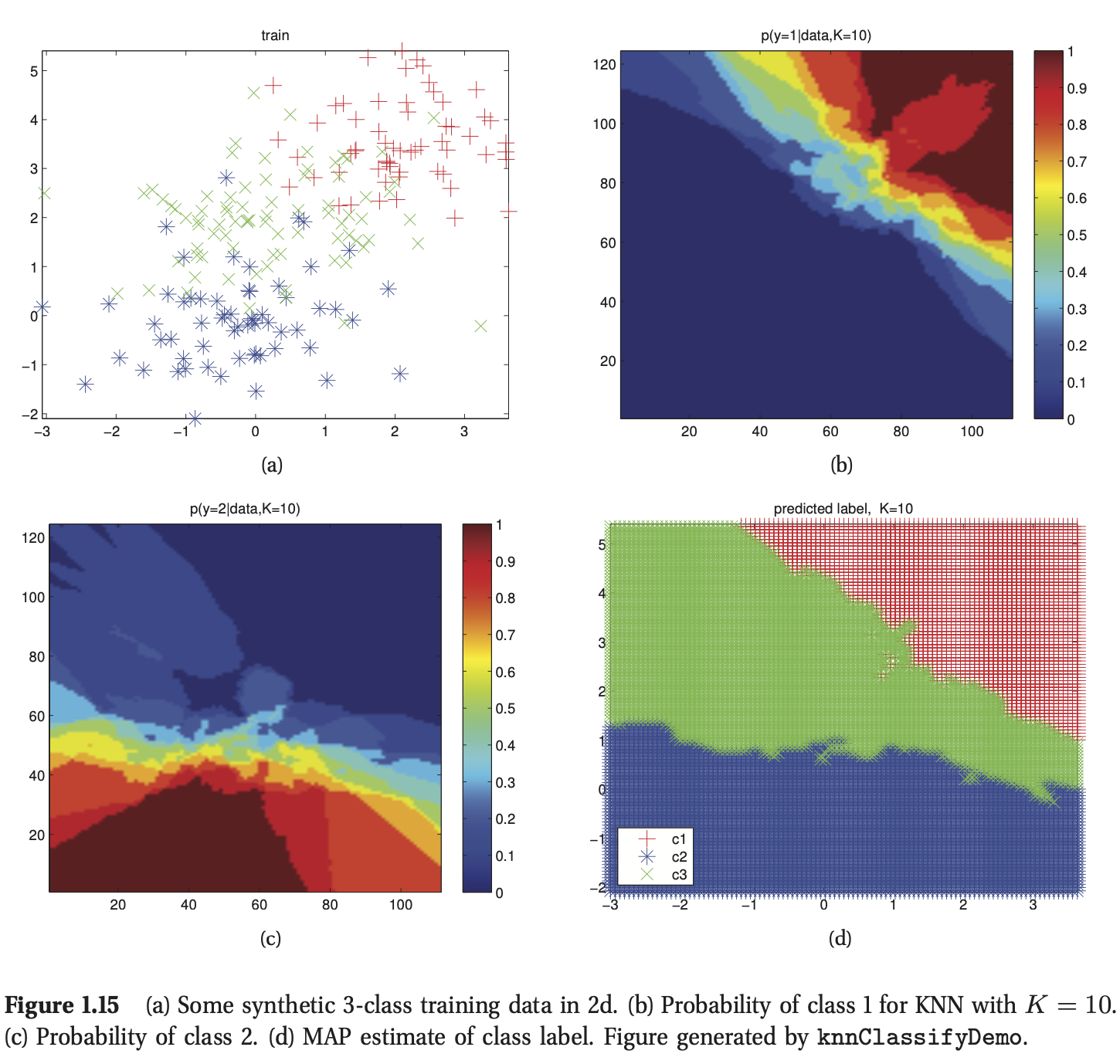
图1.15 给出了这个方法在实际使用过程中的一个例子,其中输入为2维向量,所有数据共有3类,此时我们选择K=10(我们会在后面的内容中讨论K的影响)。图(a)绘制了训练数据,图(b)绘制了\(p(y=1|\mathbf{x},\mathcal{D})\),图(c)绘制了\(p(y=2|\mathbf{x},\mathcal{D})\),我们不需要绘制\(p(y=3|\mathbf{x},\mathcal{D})\),因为每个点属于哪个类的概率满足和为1的定理。图(d)绘制了最大后验概率分布\(\hat{y}(\mathbf{x})=\arg \max_c p(y=c|\mathbf{x},\mathcal{D})\)。
当K=1时,KNN分类器将得到关于所有点的泰森多边形图(Voronoi tessellation)(见图1.14(b))。这是一种空间划分的方式,在这种方式中,每一个区域\(V(\mathbf{x}_i)\)与每一个点\(\mathbf{x}_i\)相关联,其中\(V(\mathbf{x}_i)\)中的每一个点距离\(\mathbf{x}_i\)要更近。在每一个区域中,预测的标签就是该区域关联的训练样本\(\mathbf{x}_i\)的标签。
1.4.3 维度灾难(curse of dimensionality)
KNN分类器十分简单且效果很好,其前提是需要一个好的距离测度以及足够多的标记数据。然而,KNN的劣势在于它不适用于高维输入。造成这个问题的原因是维度灾难(curse of dimensionality)。
为了解释维度灾难,我们给出一个案例。考虑一个在\(D\)维单元空间中非均匀分布的数据集,基于该数据集进行KNN的分类。为了估计测试输入\(\mathbf{x}\)的类标签所服从的分布,我们在\(\mathbf{x}\)附近建立一个超立方体,为了保证x的邻居数目达到一定的比例\(f\),我们不断放大这个超立方体。考虑到整个数据集分布在一个单元空间(体积为1)中,所以当比例\(f\)满足时,小的超立方体的体积为\(f\),那么超立方体的边长为\(e_D(f)=f^{1/D}\)。如果\(D=10\)(即输入特征维度为10),我们希望基于整个数据集10%的数据做密度估计,则\(e_{10}(0.1)=0.8\),也就是说我们需要在每个维度扩展超立方体80%。哪怕我们只需要1%的数据量,\(e_{10}(0.01)=0.63\),可以结合图1.16加深理解。因为数据在每个维度的整个范围只是1,所以当使用KNN时,这种方法不再具备局域性。换句话说,KNN需要考察最近的邻居,而当数据维度特别高时,最近的邻居实际上也很远,那么它对测试输入\(\mathbf{x}\)的估计的参考价值就很低了。
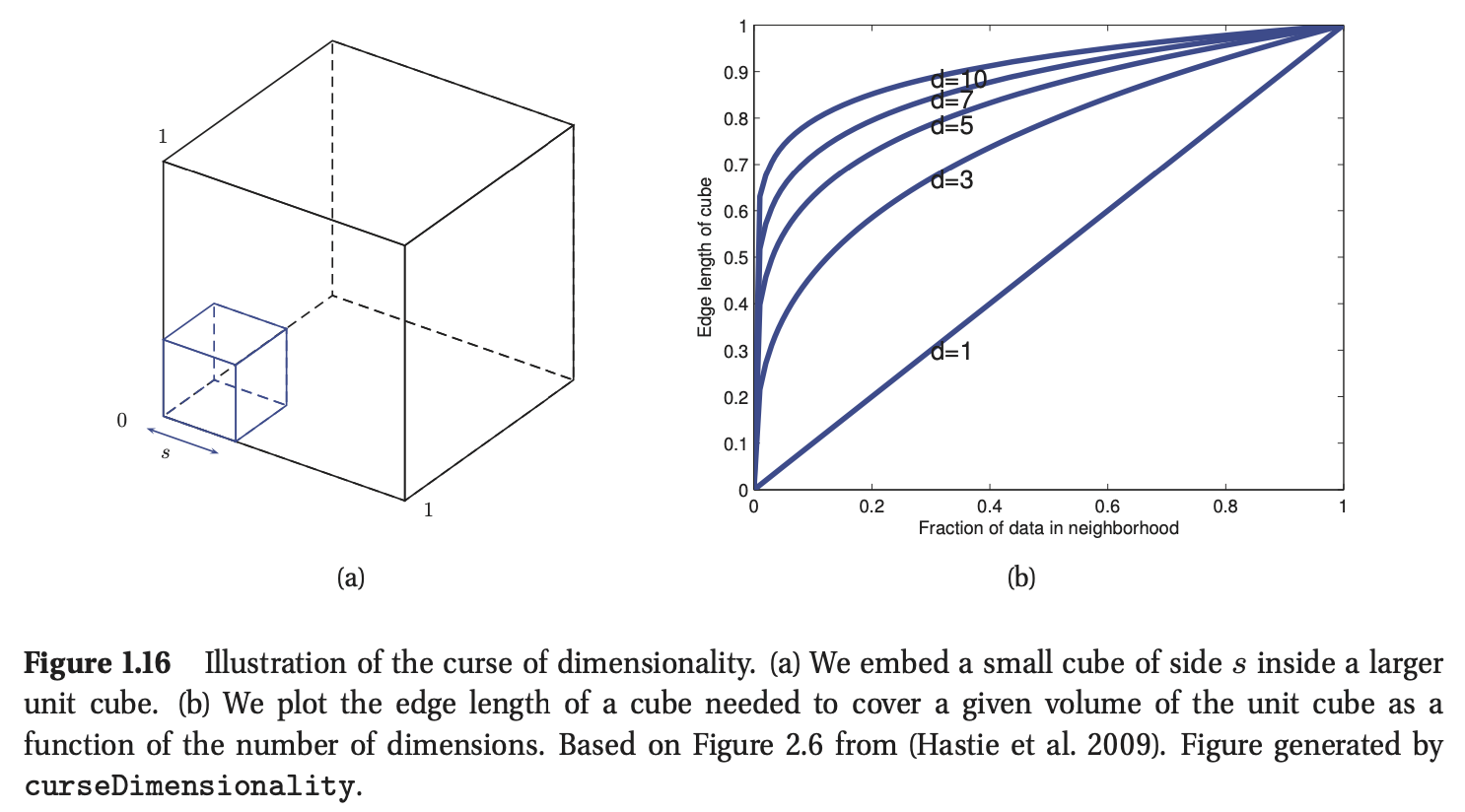
1.4.4 分类和回归中的参数模型
为了解决维度灾难的问题,一种主要的方式是对数据的分布(\(p(y|\mathbf{x})\)对应监督学习)或者\(p(\mathbf{x})\)对应无监督学习)作出一些假设。这些假设,又被称为归纳偏置(inductive bias),通常以参数模型的形式展示出来(比如我们假设数据分布服从高斯分布,那么相应的模型就由参数期望和方差决定)。接下来,我们将简要的描述两种广泛使用的参数模型;我们会在后面的内容中重新接触这些模型。
1.4.5 线性回归
在回归模型中最广泛使用的线性回归(linear regression),在这个模型中,输出是输入的线性函数。
其中\(\mathbf{w}^T\mathbf{x}\)表示输入向量\(\mathbf{x}\)与模型权重向量\(\mathbf{w}\)之间的内积,\(\epsilon\)表示预测结果与真实结果之间的残差(residual error)。
通常情况下,我们假设\(\epsilon\)服从高斯或者正态分布,符号上表示为\(\epsilon \sim \mathcal{N}(\mu,\sigma^2)\),其中\(\mu\)表示期望,\(\sigma^2\)表示方差。高斯分布的图形如图1.17(a)所示。
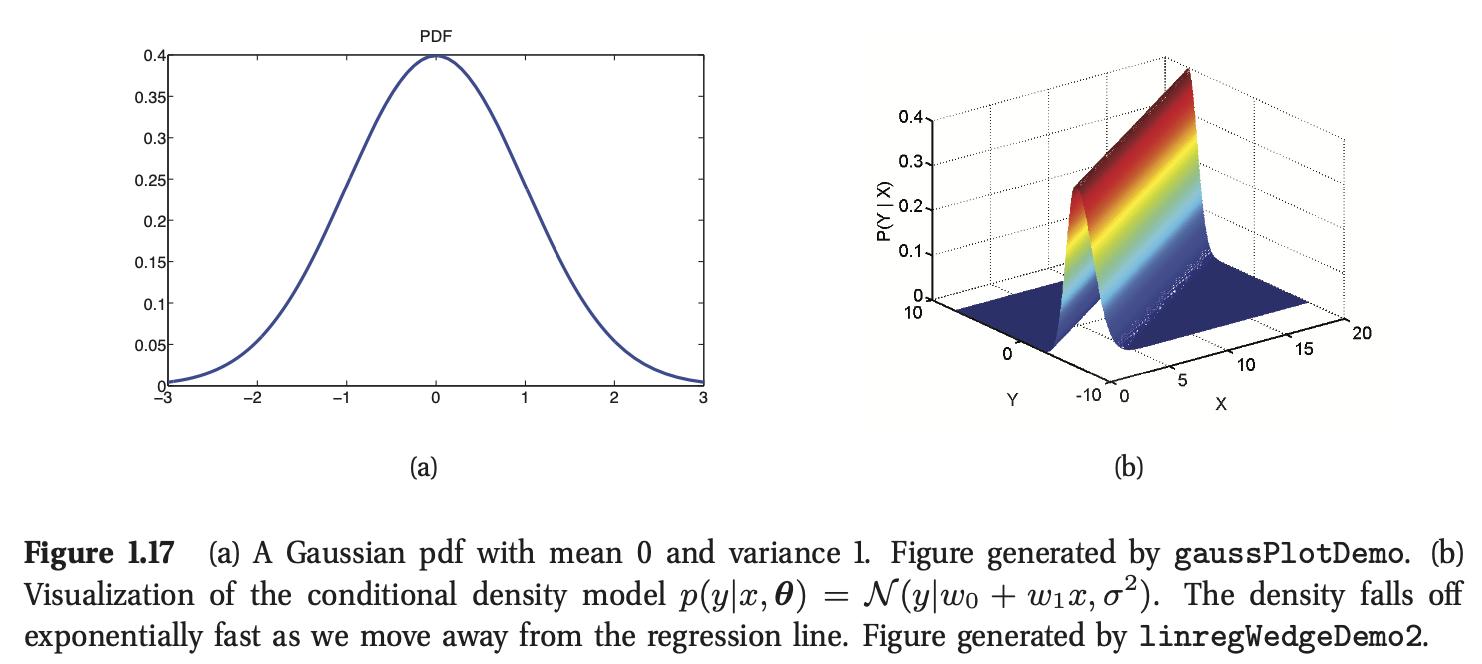
为了更加明确线性回归与高斯分布之间的联系,我们重写上述模型的形式:
根据上式我们可以发现该模型是一个条件概率密度模型。在最简单的情况下,我们假设\(\mu\)是一个关于\(\mathbf{x}\)的线性函数,即\(\mu=\mathbf{w}^T\mathbf{x}\),且噪声的与输入无关,即\(\sigma^2(\mathbf{x})=\sigma^2\)。在这种情况下,\(\mathbf{\theta}=(\mathbf{w},\sigma^2)\)为模型的参数。
举例来说,假设输入是一个一维变量。期望的输出可以表示为:
其中\(w_0\)为截距或者偏置(bias)项,\(w_1\)为斜率。在上式中,我们定义了向量\(\mathbf{x}=(1,x)\)。(在模型中,通过使用常数项1,将偏置项和其他项组合在一起是一个常用的符号上的技巧)。如果\(w_1\)大于0,意味着我们希望输出随着输入的增加而增加。图1.17(b)给出了说明。图1.7(a)给出了一个更加方便的展示方式,其中绘制了输出的期望值与\(x\)的关系。
将输入\(\mathbf{x}\)替换为关于输入的线性函数\(\phi(\mathbf{x})\),线性回归模型同样可以对非线性关系进行建模。也就是说,我们使用:
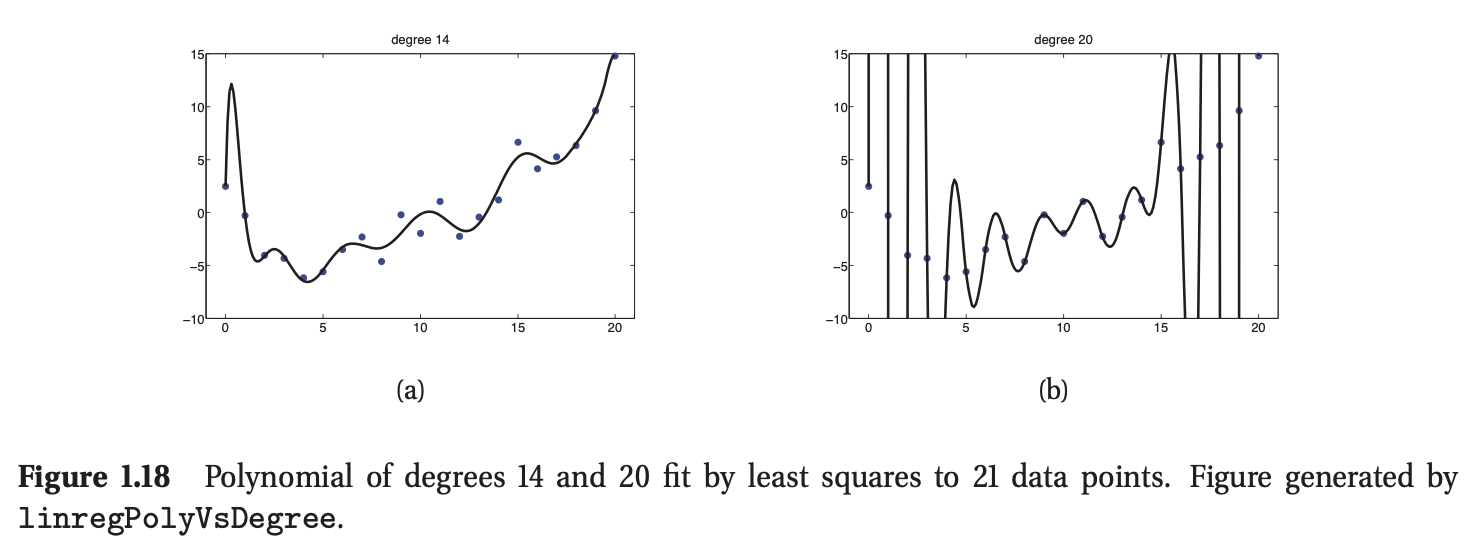
上式为称为基函数拓展(basis function expansion)。举例来说,在图1.18中,\(\phi(\mathbf{x})=[1,x,x^2,...,x^d]\),其中\(d=14\)和\(d=20\),这被称为多项式回归(polynomial regression)。我们会在后面的内容中介绍其他的基函数拓展形式。事实上,许多著名的机器学习方法——比如支持向量机,神经网络,分类和回归树等等,都可以看做是从数据中学习基函数的不同方法,我们会在第14和16章中讨论。
1.4.6 逻辑回归
我们可以将线性回归模型推广到(二元)分类问题中,为了实现这一点,我们只需要做出两点变化。首先,我们将关于\(y\)的分布替换为伯努利分布(Bernoulli),该分布对于那些目标值为二元变量的情况更加适合,即\(y\in\{0,1\}\)。也就是说,我们令:
其中\(\mu(\mathbf{x})=\mathbb{E}[y|\mathbf{x}]=p(y=1|\mathbf{x})\)。第二个改变在于,我们首先计算关于输入的线性组合,这一点与之前一样,并将结果输入到一个非线性函数中,从而确保\(0\le\mu(\mathbf{x})\le1\),即:
上式中\({\rm{sigm}}(\eta)\)为sigmoid函数,又被称为logistic或者logit函数。定义为:
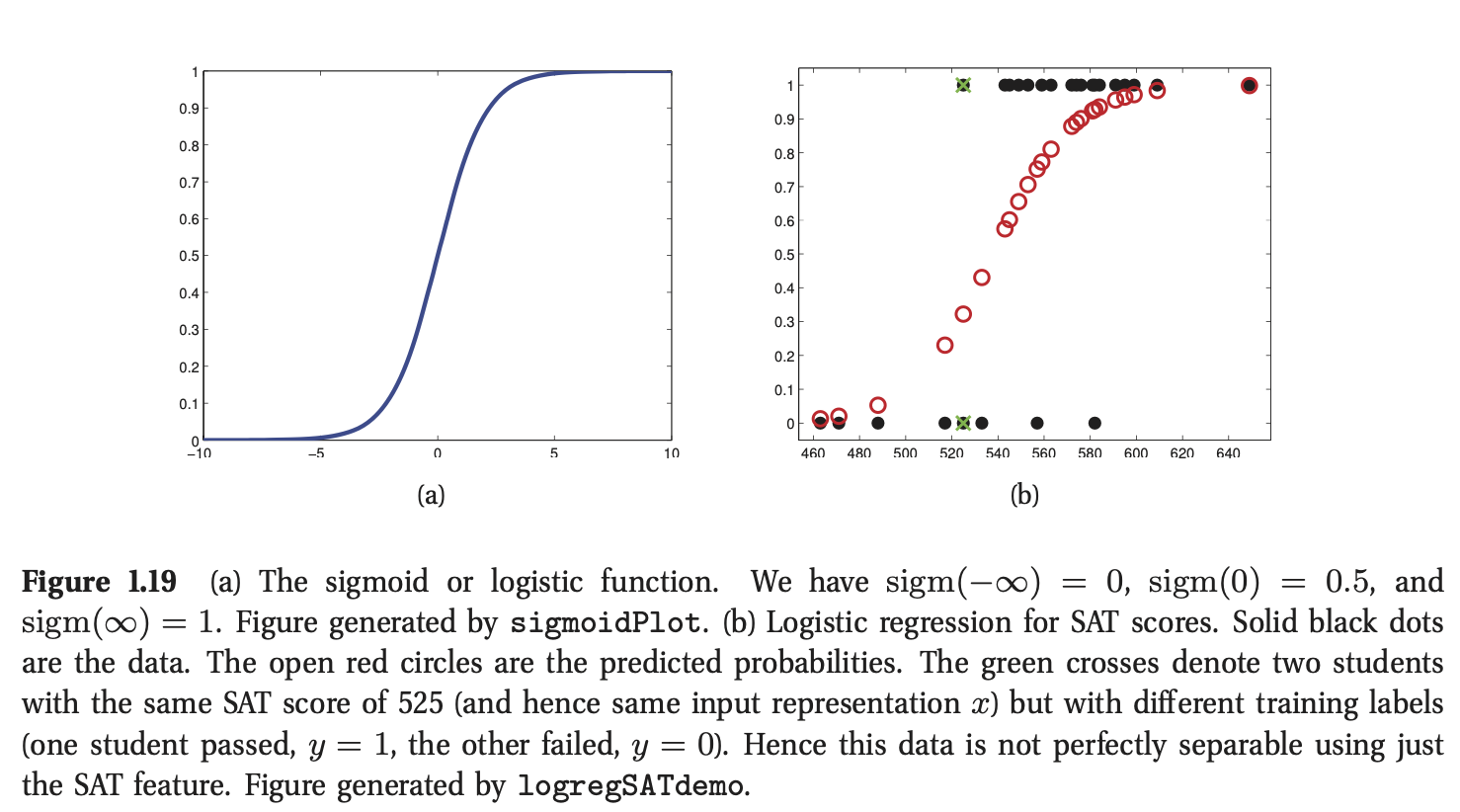
术语"sigmoid"表示S型:如图1.19(a)所示。它又被称为压缩函数,因为它将整个实轴映射到了区间\([0,1]\),这对于那些需要输出具有概率性解释的模型而言很有必要。
将上述两个改变进行统一,我们得到:
上式被称为逻辑回归,因为它与线性回归的形式十分相似(尽管它是用于分类而非回归的)。
图1.19(b)给出了一个简单的逻辑回归的例子,其中我们绘制了
\(x_i\)为学生\(i\)的SAT成绩(美国的高考),\(y_i\)表示该学生是否通过考试。黑色实心点表示训练数据,红色圆点即\(p(y=1|\mathbf{x}_i,\hat{\mathbf{w}})\),其中\(\hat{\mathbf{w}}\)表示从训练集中估计得到的参数(我们将在8.3.4节中讨论如何估计这些参数).
如果我们将0.5作为输出概率的阈值,我们可以得到一个具备如下形式的决策规则:
根据图1.19(b)我们可以发现,\({\rm{sigm}}(w_0+w_1x)=0.5\)时,对应的输入\(x\approx 545 =x^*\)。我们可以绘制一条垂线\(x=x^*\),这被称为决策边界。所有分布在边界左边的点被分类为0,右边的被分类为1.
我们发现这个决策规则在训练集上的错误率并非为0。这是因为数据并非是线性可分的。也就是说,我们没有办法通过一条直线将\(0\)和\(1\)分开。我们可以通过基函数拓展的方式获得一个非线性的决策边界,就像我们在非线性回归中所做的那样。在本书的后面,我们将看到更多相关案例。
1.4.7 过拟合(Overfitting)
当我们训练非常灵活的模型时,我们需要关注模型是否过分适应数据(过拟合),也就是说我们应该避免对输入中的任何微小的变化进行建模,因为那些微小的变化很有可能是噪音而非真实的信号。这个在图1.18(b)中可以体现,我们发现当使用一个阶数特别高的多项式拟合数据时,曲线会非常“扭曲”。真实的函数基本上不会是这样的变化趋势。因此使用这样的模型很难保证未来预测的精度。
另一个例子,考虑KNN分类器。\(K\)值对模型的性能有重要的影响。当\(K=1\)时,模型在训练集上没有任何错误(因为我们只是返回原始训练数据的标签),但最终预测的决策边界却非常“扭曲”(如图1.20(a))所示,所以这种方法在预测未来的数据时未必有效。在图1.20(b)中,我们发现当使用\(K=5\)时,最终的决策边界将会更加平滑,因为我们在一个更大的邻域内进行预测。当\(K\)不断增加时,决策边界将会更加平滑,当\(K=N\)时,我们将所有预测输入的类别都判定为训练集中占主要部分的类别。接下来,我们将讨论如何选择合适的\(K\)值。
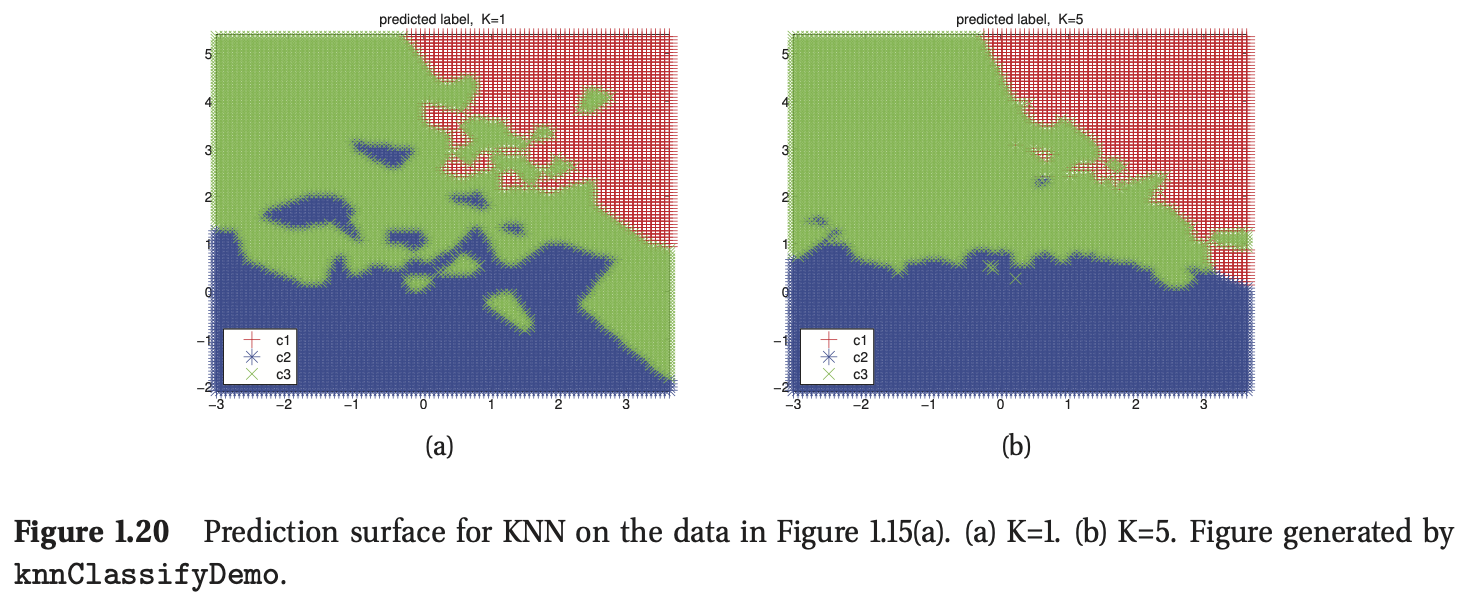
1.4.8 模型选择
当我们拥有一系列不同复杂度的模型时(比如,包含不同阶数的线性或逻辑回归模型,或者具有不同K值的KNN模型),我们该如何选择最合适的那一个呢?一个自然的方法是计算每种方法在训练集上的误分类率(misclassification rate)。定义为:
其中\(f(\mathbf{x})\)为分类器。在图1.21(a)中,我们绘制了在KNN分类器中误分类率与\(K\)的关系(点蓝线)。我们发现当\(K\)的数量增加时,训练集上的错误率将会增加。正如前文所述,如果我们选择\(K=1\),模型在训练集上的错误率为0,因为模型只是存储了训练集而已。
然而,我们真正关心的是泛化误差(generalization rate),即模型在新的数据集上的平均误分类率(见6.3节)。这个泛化误差可以近似为模型在一个大的独立的测试集(test set)上的错误率,这个测试集在模型训练过程中不被使用。我们在图1.21(a)中绘制了测试集错误率与\(K\)的关系。现在我们发现一条U-型曲线:对于复杂的模型(\(K\)比较小),模型过拟合,对于简单的模型(\(K\)值很大),模型欠拟合(underfits)。所以,一个明显的方法是挑选在测试集上错误率最小的\(K\)值(比如在这个例子中,10到100之间的取值应该都很好)。
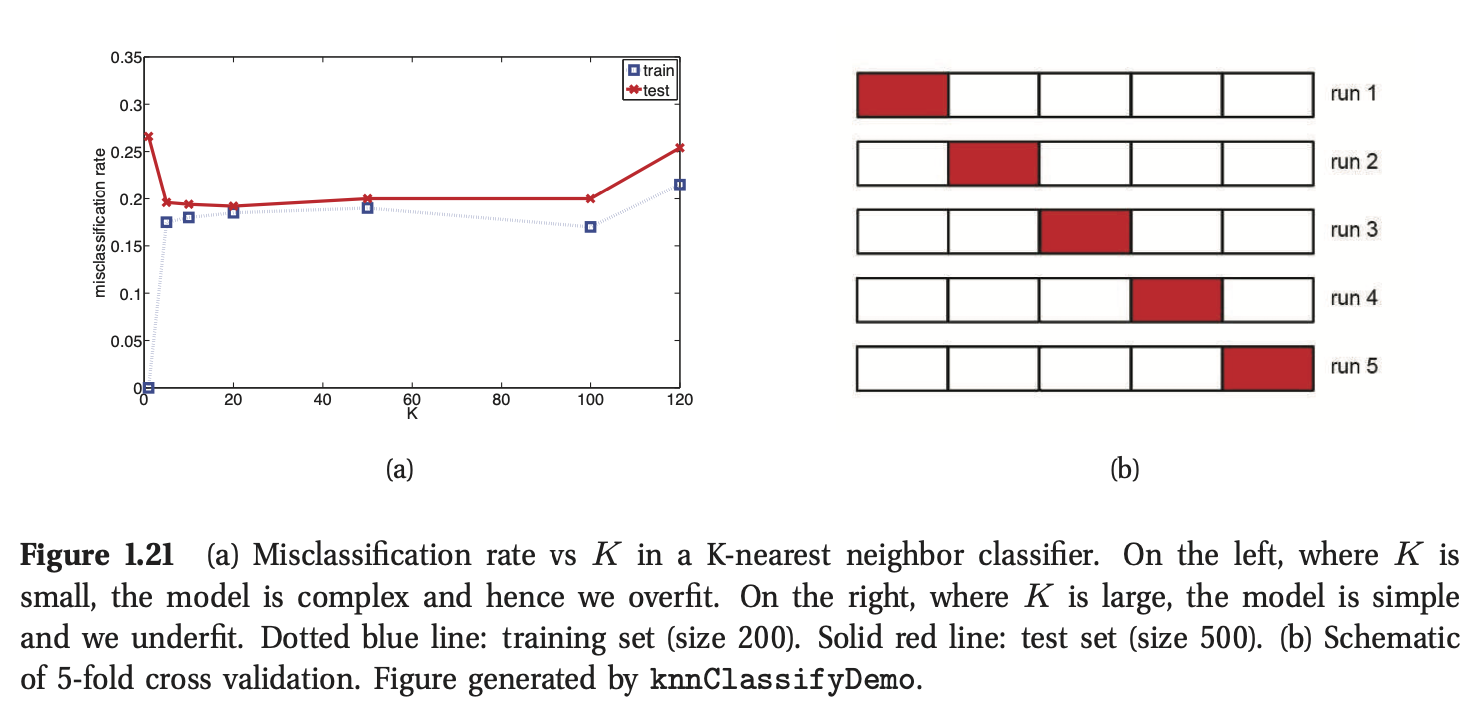
不幸的是,当我们训练模型时,我们接触不到测试集,所以我们不能使用测试集来辅助我们选择正确的模型复杂度。然而,我们可以通过将训练集分成两部分的方法创建一个测试集:一部分用于训练模型,另一部分称为验证集(validation set),用于选择模型的复杂度。我们基于训练集优化所有的模型,然后评估他们在验证集上的性能,并且选择性能最好的模型。一旦我们选择了最好的模型作为最终的模型,我们可以基于全部的数据重新优化模型。如果我们还有一个独立的测试集,我们可以基于这个测试集进行性能评估,用来估计我们模型的精度(我们将在6.5.3节介绍更多细节)。
通常情况下,我们使用80%的数据作为训练集,20%作为验证集。但是如果可以获取的训练集样本数量有限,这个技术将会面临挑战,因为模型将没有足够的数据用于训练,也不会有足够的数据用于对未来性能的合理估计。
一个简单但是著名的解决方法是使用交叉验证(cross validation)。这个思想很简单:我们将训练集分成\(K\)个包(folds);然后对于每个包\(k\in\{1,...,K\}\),我们基于除了\(k\)以外的所有包进行模型训练,然后在包\(k\)上进行测试,这个过程循环进行\(K\)次,如图1.21(b)所示。然后计算模型在所有包上的错误率的平均值,作为对测试误差的代理(值得注意的是,每个数据点只会被用来预测一次,但可以被用来训练\(K-1\)次)。通常情况下,我们使用\(K=5\),这被称为\(5-fold\) CV。如果设置\(K = N\),相应的方法被称为留一法交叉验证(leave-one out cross validation,LOOCV),因为在包\(i\)中,我们利用除了\(i\)以外的所有数据进行训练,并用数据\(i\)进行测试。
选择KNN分类器中的K值是一个更一般的问题——模型选择(model selection)的一个特例,在模型选择问题中,我们需要在具有不同复杂度的模型中作出选择。交叉验证被广泛用于解决这类问题,尽管我们会在书中介绍其他方法。
1.4.9 没有免费的午餐理论(No free lunch theorem)
All models are wrong, but some models are useful.—George Box
很多机器学习都涉及到设计不同的模型,以及使用不同的算法去训练这些模型。我们可以针对特定的问题使用诸如交叉验证的方法去选择最好的模型。然而,没有放之四海而皆好的模型——这被称为没有免费的午餐理论(no free lunch theorem)。这是因为很多假设在某个领域可能会十分奏效,在另一个领域则不尽然。
因为没有免费的午餐理论,我们需要开发不同类型的模型,去涵盖现实世界中不同领域的数据。对于每个模型,可能有很多不同算法去训练它们,且不同算法都在速度—精度—复杂度之间权衡。数据、模型和算法三者是后面章节需要学习的内容。
posted on 2023-02-22 10:23 ZhangJianhua0728 阅读(28) 评论(0) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号