2.概率论

目录

• 2.概率论
  • 2.1 前沿
  • 2.2 关于概率论的简单综述
    • 2.2.1 离散随机变量
    • 2.2.2 基本定理
      • 2.2.2.1 两个事件并集发生的概率
      • 2.2.2.2 联合概率
      • 2.2.2.3 条件概率
    • 2.2.3 贝叶斯法则
      • 2.2.3.1 案例：医疗诊断
      • 2.2.3.2 案例：生成式分类器
    • 2.2.4 独立性和条件独立性
    • 2.2.5 连续随机变量
    • 2.2.6 分位数(Quantiles)
    • 2.2.7 均值和方差
  • 2.3 一些常用的离散分布
    • 2.3.1 二项(binomial)和伯努利(Bernoulli)分布
    • 2.3.2 多项分布(multinomial distribution)和多项努利分布(multinoulli distribution)
      • 2.3.2.1 应用：DNA序列基序
    • 2.3.3 泊松分布(Poisson distribution)
    • 2.3.4 经验分布(empirical distribution)
  • 2.4 一些常用的连续分布
    • 2.4.1 高斯（正态）分布
    • 2.4.2 退化（Degenerate）pdf
    • 2.4.3 拉普拉斯分布
    • 2.4.4 伽马分布
    • 2.4.5 贝塔分布
    • 2.4.6 帕累托分布
  • 2.5 联合概率分布
    • 2.5.1 协方差和相关系数
    • 2.5.2 多元高斯
    • 2.5.3 多元学生t分布
    • 2.5.4 狄利克雷分布
  • 2.6 随机变量的变换
    • 2.6.1 线形变换
    • 2.6.2 生成变换
      • 2.6.2.1 多元变量变换*
    • 2.6.3 中心极限定理
  • 2.7 蒙特卡罗近似
    • 2.7.1 举例：变量变换，MC方式
    • 2.7.2 例子：用蒙特卡罗积分估计\(\boldsymbol{\pi}\)
    • 2.7.3 蒙特卡罗近似的精度
  • 2.8 信息理论
    • 2.8.1 熵
    • 2.8.2 KL散度
    • 2.8.3 互信息
      • 2.8.3.1 连续随机变量的互信息*

2.概率论

2.1 前沿

Probability theory is nothing but common sense reduced to calculation. —— Pierre Laplace

在前面的章节中，我们已经了解了概率论在机器学习中所扮演的有用的角色。本章，我们将讨论更多关于概率论的细节。我们并没有足够的篇幅展开相关领域的深层次讨论——读者可以自行参考更多的相关书籍。但在后面的章节中，我们将简明扼要的介绍许多可能会用到的关键思想。

在我们探讨更多技术方面的细节之前，请容许我们思考一个问题：什么是概率？我们对于诸如“一个硬币面朝上的概率为0.5”的表述已经非常熟悉。但这句话到底意味着什么？关于概率至少有两种不同的解释。一种是频率（frequentist）学派的解释。在这种观点中，概率代表事件在长时间实验的情况下出现的频率。比如，在前面的例子中，我们是指如果我们投掷一枚硬币很多次，那么我们相信有一半的时间硬币的正面朝上。

另一个关于概率的解释为贝叶斯（Bayesian）学派的解释。在这种观点中，概率是用来量化我们对于某些事件的不确定度（uncertainty），所以本质上它与信息而非重复的实验相关。从贝叶斯学派的观点看待上述的例子，意味着我们相信在下一次投掷硬币时，硬币正面朝上的可能性为0.5。

贝叶斯解释的一个重要优势在于，它可以用来衡量那些无法进行重复试验的事件的不确定度。比如说我们希望估计到2020年冰川融化的概率。这个事件本身可能只发生一次甚至不会发生，也就是说它是不能被重复的试验。然而，我们可以量化针对该事件发生的不确定度（比如说基于我们采取的一些抑制全球变暖的行为，我们可以认为这个事件发生的可能性会变小）。再比如第1章中提及的垃圾邮件分类任务，我们可能已经收到一个特定的邮件信息，我们希望计算它是垃圾邮件的可能性。或者我们在雷达屏幕上观察到一个移动光点，我们希望计算这个飞行物身份的概率分布（它是一只鸟还是一个飞机呢？）。在上述的所有案例中，尽管没有一个事件是可以重复试验的，但贝叶斯观点却是有效且具备天然可解释性的。所以在本书中我们将采用贝叶斯观点对概率的解释。不过幸运的是，无论我们采取哪一种观点去看待概率，概率论的基本规则都是一样的。

2.2 关于概率论的简单综述

本章介绍关于概率论基础的一些知识，仅仅针对那些对相关知识已经生疏的读者。关于更多的相关细节，可以参考其他的相关书籍。已经对这块知识比较熟悉的读者可以直接跳过本章。

2.2.1 离散随机变量

表达式\(p(A)\)表示事件\(A\)发生的概率。比如\(A\)可能表示"明天会下雨"。其中\(p(A)\)满足\(0\le p(A)\le1\)，如果\(p(A)=0\)，表示事件\(A\)不可能发生，\(p(A)=1\)意味着事件\(A\)肯定发生。我们使用\(p(\bar A)\)表示事件非\(A\)发生的可能性，满足\(p(\bar A)=1-p(A)\)。通常情况下，我们将"\(A\)发生"这个事件写作\(A=1\)，"\(A\)不发生"写作\(A=0\)。

通过定义离散随机变量（discrete random variable）\(X\)，我们可以扩展二元事件（即事件只存在两种状态）的符号表达，该离散变量取值于一个有限集或者可数无限集 \(\chi\)(译者注：关于可数无限集的例子：比如做一个抛掷硬币的试验，直到第一次出现正面时抛掷硬币的次数\(\chi\)的取值所构成的就是一个可数无限集)。我们将事件\(X=x\)发生的概率表示为\(p(X=x)\)，或者直接写成\(p(x)\)。其中符号\(p()\)称为概率质量函数(probability mass function),满足性质\(0 \le p(x) \le 1,\sum_{x\in\chi}p(x)=1\)。图2.1展示了定义在一个有限状态空间(state space)\(\chi = \{1,2,3,4\}\)上的两种概率质量函数。其中左图属于均匀分布,\(p(x)=1/4\)，右图为一个退化分布\(p(x)=\mathbb{I}(x=1)\)，其中\(\mathbb{I}()\)为二元指示函数(indicator function)，这个分布意味着\(X\)永远等于1，换句话说，它是一个常数。

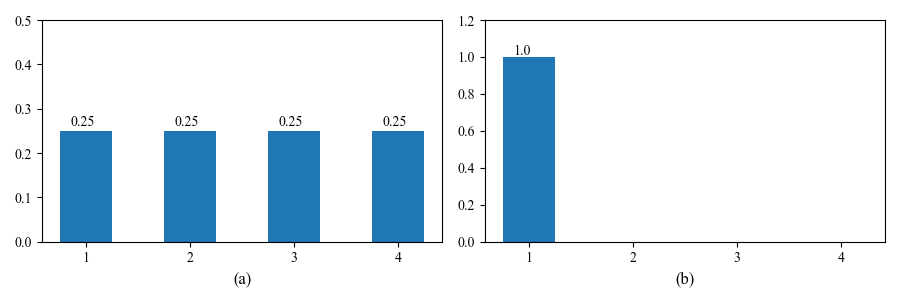
图2.1（a）是{1, 2, 3, 4}上的均匀分布，其中\(p(x = k) = 1/4\)。 (b) 退化分布\(p(x) = 1\) if \(x = 1\)，\(p(x) = 0\) if \(x ∈ \left\{2, 3, 4\right\}\)。 由 discreteProbDistFig 生成的数字。

import numpy as np
import matplotlib.pyplot as plt

plt.rc('font', family='Times New Roman')

X=[1,2,3,4]
X2=[1]
bins=[1,2,3,4,5]

fig, ax = plt.subplots(1,2,figsize=(9,3))
n1=ax[0].hist(X,bins=bins,align='left',rwidth=0.5,density=True)[0]
print(n1)
ax[0].set_ylim([0,0.5])
ax[0].set_xticks([1,2,3,4])
for i,j in zip(bins[:len(n1[n1>0])],n1[n1>0]):
	ax[0].text(i-0.15,j+0.01,str(j))
ax[0].set_xlabel('(a)',fontsize=12,weight='normal')

n2=ax[1].hist(X2,bins=bins,align='left',rwidth=0.5,density=True)[0]
ax[1].set_ylim([0,1.2])
ax[1].set_xticks([1,2,3,4])
for i,j in zip(bins[:len(n2[n2>0])],n2[n2>0]):
	ax[1].text(i-0.15,j+0.01,str(j))
ax[1].set_xlabel('(b)',fontsize=12,weight='normal')
	
plt.tight_layout()
plt.savefig('./discreteProbDistFig.png')
plt.show()

2.2.2 基本定理

本章，我们将介绍概率论的基本定理。

2.2.2.1 两个事件并集发生的概率

给定两个事件\(A\)和\(B\)，定义事件\(A\)或\(B\)发生的概率为：

\[\begin{align} p(A\or B) &= p(A)+p(B)-p(A\and B) \tag{2.1} \\ &=p(A)+p(B) \ 如果A和B互斥 \tag{2.2} \\ \end{align} \]

2.2.2.2 联合概率

我们定义事件\(A\)和\(B\)同时发生的概率为：

\[p(A,B)=p(A\and B)=p(A|B)p(B) \tag{2.3} \]

上式通常又被称为乘法法则(product rule)。给定两个事件的联合概率分布（joint distribution）\(p(A,B)\)，定义边缘分布(marginal distribution)如下:

\[p(A)=\sum_b p(A,B)=\sum_b p(A|B=b)p(B=b) \tag{2.4} \]

上式我们针对事件\(B\)所有的可能状态进行求和。类似地，我们也可以定义\(p(B)\)，这通常被称为求和法则（sum rule）或者叫全概率法则（rule of total probability）。

我们可以多次使用乘法法则，进而引出概率论中的链式法则（chain rule）：

\[p(X_{1:D})=p(X_1)p(X_2|X_1)p(X_3|X_2,X_1)...p(X_D|X_{1:D-1}) \tag{2.5} \]

式中，我们模仿了Matlab中的一种符号写法\(1:D\)表示集合\(\{1,2,…,D\}\)。

2.2.2.3 条件概率

我们定义在事件\(B\)发生的前提下，事件\(A\)发生的概率为条件概率（conditional probability）：

\[p(A|B)=\frac{p(A,B)}{p(B)} \ {\rm{if}} \ p(B)\gt 0 \tag{2.6} \]

2.2.3 贝叶斯法则

根据求和法则和求积法则，结合条件概率的定义，可以得到贝叶斯法则（Bayes’ rule）或者贝叶斯定理（Bayes’ Theorem）。

\[p(X=x|Y=y)=\frac{p(X=x,Y=y)}{p(Y=y)}=\frac{p(X=x)p(Y=y|X=x)}{\sum_{x^\prime}p(X=x^\prime)p(Y=y|X=x^\prime)} \tag{2.7} \]

Sir Harold Jeffreys指出“贝叶斯定理之于概率论等价于勾股定理之于几何学” 。我们在下面将介绍两个贝叶斯理论的应用，但在全书后面的内容中，我们将会碰到很多相关的例子。

2.2.3.1 案例：医疗诊断

考虑一个关于使用贝叶斯法则的案例：医疗诊断问题。假设你是一个40多岁的女性，你决定去做一个名叫manmogram检测,以判断自己是否患有乳腺癌。如果检测结果显示为阳性，那么你患病的概率有多大？这个问题的答案显然与检测方法的可靠性有关。假设你被告知检测方法的敏感性(sensitivity)为80%，也就是说，如果你患有癌症，那么测试结果显示为阳性的可能性为0.8。换句话说：

\[p(x=1|y=1)=0.8 \tag{2.8} \]

其中\(x=1\)表示检测结果为阳性，\(y=1\)表示你确实患有乳腺癌。许多人因此就认为他们患有癌症的可能性为80%。但这是错误的！因为他们忽略了患有乳腺癌的先验概率，幸运的是，这个概率相当低：

\[p(y=1)=0.004 \tag{2.9} \]

忽略先验概率的情况被称为基率谬论(base rate fallacy)。我们同样需要考虑测试结果可能是假正例(false positive)或者误警报(false alarm)的情况。不幸的是，类似这样的假正例发生的可能性还很高(在现有的筛选技术下)：

\[p(x=1|y=0)=0.1 \tag{2.10} \]

将上述三项通过贝叶斯法则进行合并，我们可以计算出正确的答案：

\[\begin{align} p(y=1|x=1) & = \frac{p(x=1|y=1)p(y=1)}{p(x=1|y=1)p(y=1)+p(x=1|y=0)p(y=0)} \tag{2.11} \\ & = \frac{0.8 \times 0.004}{0.8 \times 0.004 + 0.1 \times 0.996} \tag{2.12} \end{align} \]

其中\(p(y=0)=1-p(y=1)=0.996\)。换句话说，如果你的检测结果为阳性，你也只有大概3%的可能性患有乳腺癌。(该案例中的数据来自于相关文献，基于该项分析，美国政府决定不再推荐女性在40岁时进行每年的mammogram检测：因为假正例会导致不必要的担心和压力，并最终导致不必要的，昂贵的，并且可能存在潜在伤害的后续检测。5.7节将介绍当我们在不确定的情况下权衡利弊的最优方法)。

2.2.3.2 案例：生成式分类器

我们可以将医疗诊断的例子一般化，从而实现对任意形式的特征向量\(\mathbf{x}\)进行分类：

\[p(y=c|\mathbf{x})=\frac{p(y=c)p(\mathbf{x}|y=c)}{\sum_{c^\prime}p(y=c^\prime|\mathbf{\theta})p(\mathbf{x}|y=c^\prime)} \tag{2.13} \]

上式被称为生成式分类器(generative classifier)，因为它通过使用类条件概率密度\(p(\mathbf{x}|y=c)\)和类先验分布\(p(y=c)\)来指定如何生成样本。我们会在第3章和第4章详细讨论这一类模型。与该模型不同的时，判别式分类器直接对类后验概率分布\(p(y=c|\mathbf{x})\)进行训练。我们会在8.6节讨论两种方法的优缺点。

2.2.4 独立性和条件独立性

如果两个随机变量\(X\)和\(Y\)的联合概率分布可以表示为边缘分布的乘积，则称\(X\)和\(Y\)是无条件独立(unconditionally independent)或者边缘独立(marginally independent)的，

\[X \perp Y \Leftrightarrow p(X,Y)=p(X)p(Y) \tag{2.14} \]

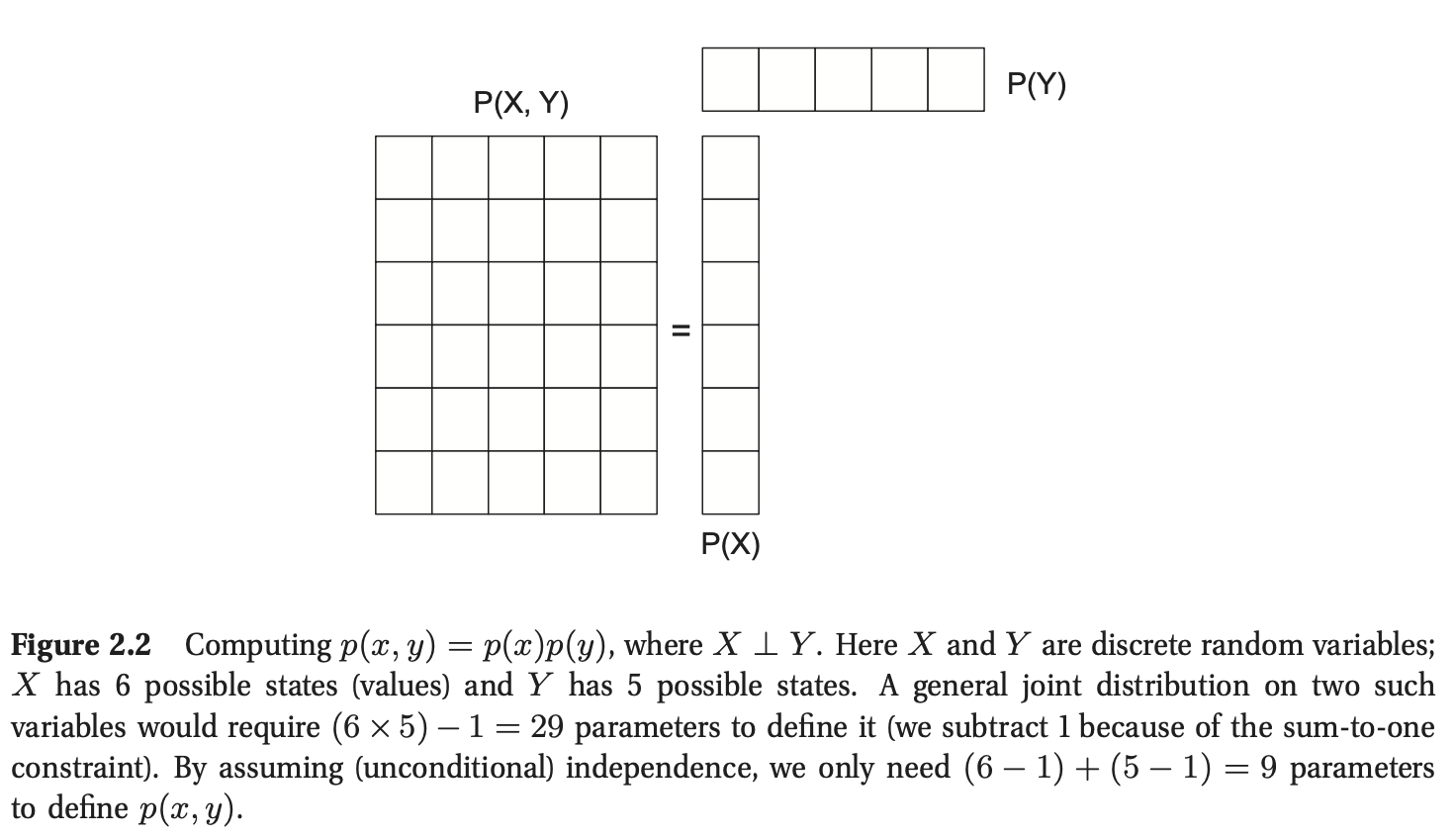
一般情况下，我们称一系列变量之间是互相独立的，如果其联合概率分布等于各个边缘分布的乘积。
不幸的是，无条件独立很少会发生，因为大部分变量会相互影响。然而，这种影响可以通过其他变量间接产生。因此我们称已知\(Z\)的情况下,\(X\)和\(Y\)是条件独立(conditionally independent,CI)的，其成立的充要条件是条件联合分布等于条件边缘分布的乘积：

\[X \perp Y |Z \Leftrightarrow p(X,Y|Z)=p(X|Z)p(Y|Z) \tag{2.15} \]

我们在第10章会讨论图模型，届时我们可以发现这种关系可以表示为一种图结构 \(X-Z-Y\)，该图反映出\(X\)和\(Y\)之间的所有关联性都需要通过\(Z\)。举例来说，如果已经知道今天是否会下雨(\(Z\))，那么明天将会下雨的概率(事件\(X\))与今天的地是否潮湿(事件\(Y\))之间是独立的。直觉上，因为\(Z\)同时导致了\(X\)和\(Y\)，所以如果已经知道了\(Z\)，那么为了了解\(X\)，我们并不需要关于\(Y\)的信息，反之亦然。我们将会在第10章进行展开讨论。
条件独立的另一个特性为：

定理2.2.1 \(X \perp Y | Z\) 当且仅当存在函数\(g\)和\(h\)满足：

\[p(x,y|z) = g(x,z)h(y,z) \tag{2.16} \]

对于所有的\(x,y,z\)成立，且\(p(z)>0\).

条件独立性假设允许我们通过一些局部信息去构建大规模的概率模型。本书中将介绍大量的相关案例，特别是在3.5节，我们将会讨论朴素贝叶斯分类器，在17.2节，会讨论马尔可夫模型，在第10章讨论图模型;所有这些模型都充分应用了条件独立性的性质。

2.2.5 连续随机变量

截至目前，我们只是讨论了关于离散变量的情况。本节将介绍有关连续变量的相关内容。

假设\(X\)是某个未知的连续变量。变量\(X\)满足\(a \le X \le b\)的概率可以通过如下的方式进行计算。 接下来，我们定义三个事件 \(A=(X \le a), B=(X \le b), W=(a \lt X \lt b)\). 显然，我们有 \(B = A \vee W\)， 因为事件\(A\)和事件\(B\)是互斥的，根据概率论的球和法则，我们有：

\[p(B) = p(A) + p(W) \tag{2.17} \]

所以

\[p(W) = p(B) - p(A) \tag{2.18} \]

接下来定义函数\(F(q) \triangleq p(X\leq q)\). 该函数被称为累积分布函数(cumulative distribution function, cdf)，属于非单调递减函数。 图2.3(a)给出了示意图。基于该定义，我们有：

\[p(a \lt X \le b)=F(b)-F(a) \tag{2.19} \]

定义\(f(x)=\frac{d}{dx}F(x)\)(不妨假设导数确实存在)，该式被称为概率密度函数(probability density function, pdf)。 图2.3(b)给出了示意图。 在已知概率密度函数的情况下，我们可以计算一个连续变量属于某个有限区间的概率:

\[p(a \lt X \le b)=\int_a^b f(x)dx \tag{2.20} \]

如果该区间足够小，我们可以有:

\[p(x \le X \le x+dx) \approx p(x)dx \tag{2.21} \]

其中\(p(x) \ge 0\),但对于任意给定的\(x\), \(p(x) \gt 1\)是可能存在的，只要积分等于1即可。举例来说，考虑一个均匀分布(uniform distribution)\(Unif(a,b)\):

\[Unif(x|a,b)=\frac{1}{b-a}\mathbb{I}(a \le x\le b) \tag{2.22} \]

如果我们令\(a=0,b=\frac{1}{2}\)，我们有\(\forall x\in [0,\frac{1}{2}], p(x)=2\).

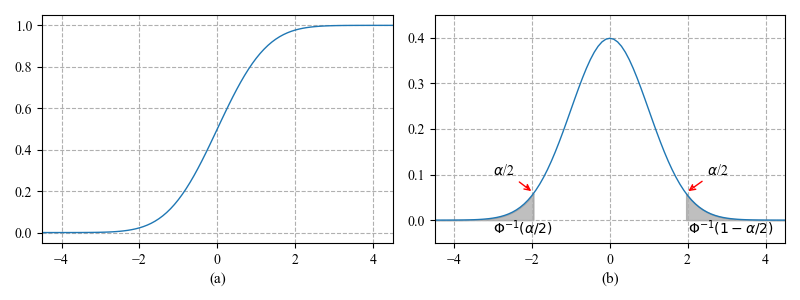
图2.3（a）标准法线的cdf图，\(N(0,1)\)。（b）相应的pdf。 每个阴影区域都包含概率质量的\(α/2\)。 因此，无阴影区域包含概率质量的\(1-α\)。 如果分布是高斯\(N(0,1)\)，那么最左边的截止点是\(\Phi^{−1}(α/2)\)，其中\(\Phi\)是高斯的cdf。 通过对称，右截止点是\(\Phi^{−1}(1 − α/2)=−\Phi^{−1}(α/2)\)。 如果\(α = 0.05\)，中心区间为95%，左截止值为-1.96，右侧为1.96。

2.2.6 分位数(Quantiles)

如果累积分布函数\(F\)是一个单调递增函数，那么它必然存在一个逆函数，定义为\(F^{-1}\)。 如果\(F\)是关于变量\(X\)的cdf，则\(F^{-1}(\alpha)=x_\alpha\)满足\(p(X\le x_\alpha)=\alpha\)，\(x_\alpha\)被称为函数\(F\)的\(\alpha\)分位数。常用的分位数包括，\(F^{-1}(0.5)\)为分布的中位数(median)，也就是说一半的概率质量分布在左边，另一半分布在右边。

我们还可以使用逆cdf来计算尾部区域概率。 例如，如果\(\Phi\)是高斯分布\(\mathcal{N}(0,1)\)的cdf，那么\(\Phi^{−1}(α/2)\)左侧的点包含\({α/2}\)概率质量，如图2.3(b)所示。 通过对称性，\(\Phi^{-1}(1−α/2)\)右侧的点也包含质量的\(α/2\)。 因此，中心区间\((\Phi^{−1}(α/2), \Phi^{−1}(1 − α/2))\)包含\(1 − α\)的质量。 如果我们设置\(α = 0.05\)，中心95%区间被范围覆盖。

\[(\Phi^{-1}(0.025),\Phi^{-1}(0.0975))=(-1.96,1.96) \tag{2.23} \]

如果分布为\(\mathcal{N}(μ，σ^2)\)，则95%的区间变为\((μ − 1.96σ，μ + 1.96σ)\)。 这有时是通过写\(μ±2σ\)来近似的。

2.2.7 均值和方差

一个分布最常见的性质是它的均值（mean）或期望值（expected value）表示为\(\mu\)。离散的随机变量的均值定义为\(\mathbb{E}[X] \triangleq \sum_{x \in \chi}xp(x)\)，连续随机变量的均值定义为\(\mathbb{E}\triangleq \int_{\chi}xp(x)dx\)，如果这个积分不是有限的，平均值则未被定义。

方差（variance）是对分布的“扩散”的度量，用\(σ^2\)表示。定义如下：

\[\begin{align*} var[X] &\triangleq \mathbb{E}[(X-\mu)^2] = \int(x-\mu)^2p(x)dx \tag{2.24} \\ &= \int x^2p(x)dx+\mu^2\int p(x)dx - 2\mu \int xp(x)dx = \mathbb{E}[X^2]-\mu^2 & \tag{2.25} \end{align*} \]

从中我们可以推导出有用的结果

\[\mathbb{E}{[X^2]} = \mu^2+\sigma^2 \tag{2.26} \]

标准差（standard deviation）被定义为

\[{\rm std}[X] \triangleq \sqrt{{\rm var}[X]} \tag{2.27} \]

这非常有用，因为它的单位与\(X\)本身相同。

2.3 一些常用的离散分布

在本节中，我们回顾一些常用的参数分布定义在离散状态空间，有限和可数无限。

2.3.1 二项(binomial)和伯努利(Bernoulli)分布

假设我们掷硬币\(n\)次。 设$ X \in \left{0,\ldots,n \right}\(为正面的次数。 如果正面的概率是\)θ\(，那么我们说\)X\(有一个二项式分布，写为\)X \sim {\rm Bin}(n,\theta)$。 pmf为

\[\begin{align} {\rm Bin}(k|n,\theta) \triangleq \left( \begin{matrix} n\\k \end{matrix} \right)\theta^k(1-\theta)^{n-k} \tag{2.28} \end{align} \]

其中

\[\left(\begin{matrix} n\\k \end{matrix} \right) \triangleq \cfrac{n!}{(n-k)!k!} \tag{2.29} \]

是从n个项目中选择k个项目的方法的数量(这被称为二项式系数(binomial coeffcient)，发音为“n选k”)。二项分布的一些例子见图2.4。该分布的均值和方差如下:

\[{\rm mean} = \theta \quad \quad {\rm var}=n\theta(1-\theta) \tag{2.30} \]

现在假设我们只抛一次硬币。设\(X \in \{0,1\}\)是一个二元随机变量，\(θ\)有“成功”或“正面”的概率。我们说\(X\)是伯努利分布(Bernoulli)。写为\(X \sim {\rm Ber}(\theta)\)，其中pmf定义为

\[{\rm Ber}(x|\theta)=\theta^{\mathbb{I}(x=1)}(1-\theta)^{\mathbb{I}(x=0)} \tag{2.31} \]

换而言之，

\[\begin{equation} \tag{2.32} {\rm Ber}(x|\theta) = \left\{ \begin{array}{lr} \theta & {\rm if}\ x=1 \\ 1-\theta & {\rm if}\ x=0 \end{array} \right. \end{equation} \]

这显然是\(n = 1\)的二项分布的特例。

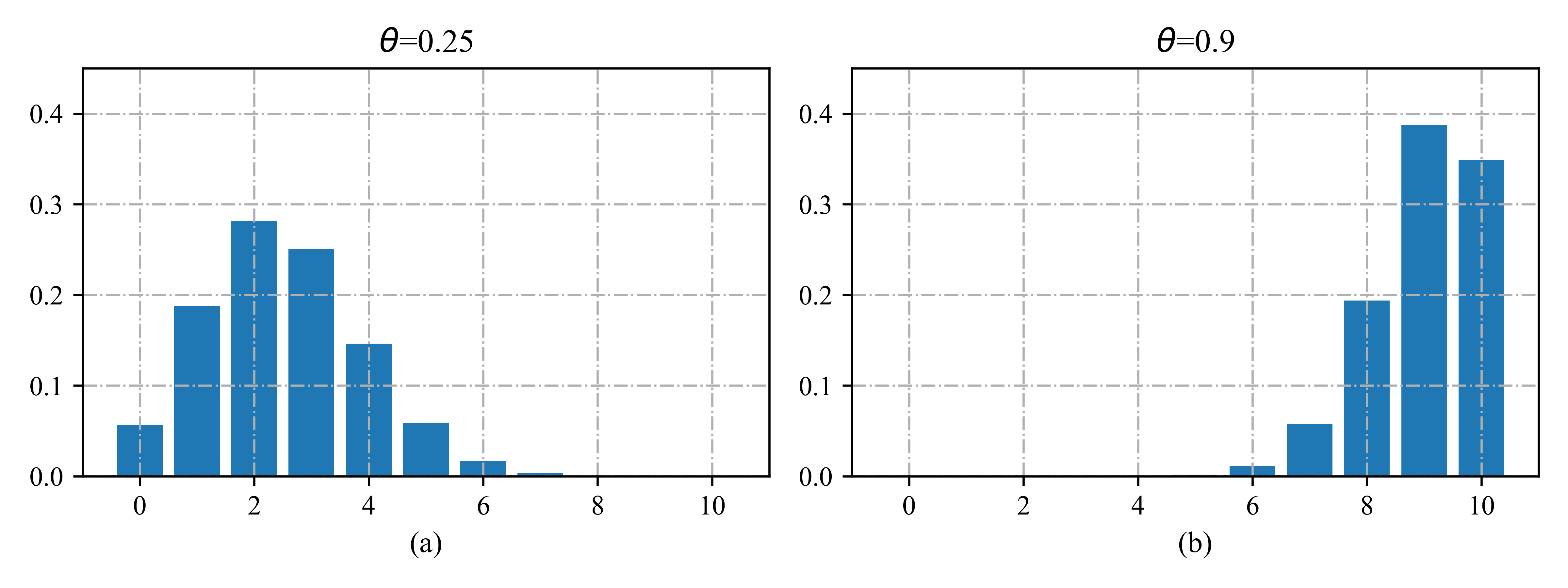
图2.4 \(n = 10\)且\(\theta \in \{0.25,0.9\}\)的二项分布

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
plt.rc('font',family='Times New Roman')

p=[0.25,0.9]
n=10
y1 = stats.binom.pmf(np.arange(0,n+1,1),n,p[0])
y2 = stats.binom.pmf(np.arange(0,n+1,1),n,p[1])

_,axes = plt.subplots(1,2,figsize=(8,3))
plt.sca(axes[0])
plt.bar(np.arange(0,n+1,1),y1)
plt.axis([-1,11,0,0.45])
plt.xlabel("",fontsize=11)
plt.ylabel("",fontsize=11)
plt.tight_layout()
plt.grid(linestyle='-.')
plt.title(r'$\theta$=0.25')
plt.xlabel('(a)')

plt.sca(axes[1])
plt.bar(np.arange(0,n+1,1),y2)
plt.axis([-1,11,0,0.45])
plt.xlabel("",fontsize=11)
plt.ylabel("",fontsize=11)
plt.tight_layout()
plt.grid(linestyle='-.')
plt.title(r'$\theta$=0.9')
plt.xlabel('(b)')

plt.savefig('./binomDistPlot.png',dpi=600)
plt.show()

2.3.2 多项分布(multinomial distribution)和多项努利分布(multinoulli distribution)

二项分布可以用来模拟抛硬币的结果。为了模拟投掷\(k\)面骰子的结果，我们可以使用多项分布。定义如下:设\(\mathbf{x}=(x_1,\ldots,x_K)\)为随机向量，其中\(x_j\)为骰子\(j\)面出现的次数。那么\(\mathbf x\)有如下的pmf:

\[{\rm Mu}(\mathbf{x}|n,\boldsymbol{\theta}) \triangleq \left( \begin{matrix} n \\ x_1 \ldots x_K \end{matrix} \right)\prod_{j=1}^K \theta_j^{x_j} \tag{2.33} \]

\(θ_j\)是边\(j\)出现的概率。

\[\left(\begin{matrix} n \\ x_1 \ldots x_K \end{matrix} \right) \triangleq \cfrac{n!}{x_1!x_2!\cdots x_K!} \tag{2.34} \]

多项式系数(multinomial coeffcient)是将数据集划分成子集方式的种类。

现在假设\(n = 1\)。这就像滚动一次\(k\)面骰子，因此\(\mathbf{x}\)将是0和1的向量(位向量)，其中只有一个位可以在上面。具体来说，如果骰子显示为面\(k\)，那么第\(k\)位将在上。在这种情况下，我们可以认为\(x\)是一个具有\(K\)个状态(值)的标量分类随机变量，\(\mathbf x\)是它的虚拟编码(dummy encoding)，即\(\mathbf{x}=[\mathbb{I}(x=1),\ldots,\mathbb{I}(x = K)]\)。例如，如果\(K = 3\)，我们将状态1、2和3编码为\((1,0,0)\)、\((0,1,0)\)和\((0,0,1)\)。这也被称为独热编码(one-hot encoding)，因为我们假设K条“线”中只有一条是“热的”或开着的。在这种情况下，pmf变成

\[{\rm Mu}({\rm x}|1,\theta) \triangleq \prod_{j=1}^K\theta_j^{\mathbb{I}(x_j=1)} \tag{2.35} \]

这种非常常见的特殊情况被称为分类分布(categorical)或离散(discrete)分布。(Gustavo Lacerda建议我们称其为多项努利分布，类似于我们将在本书中采用的二项/伯努利。)我们在这种情况下将使用以下符号:

\[{\rm Cat}(x|\boldsymbol{\theta}) \triangleq {\rm Mu}(\mathbf{x}|1,\boldsymbol{\theta}) \tag{2.36} \]

换而言之，如果\(x\sim {\rm Cat}(\boldsymbol{\theta})\)，则\(p(x=j|\boldsymbol{\theta})=\theta_{j}\)。具体参见表2.1。

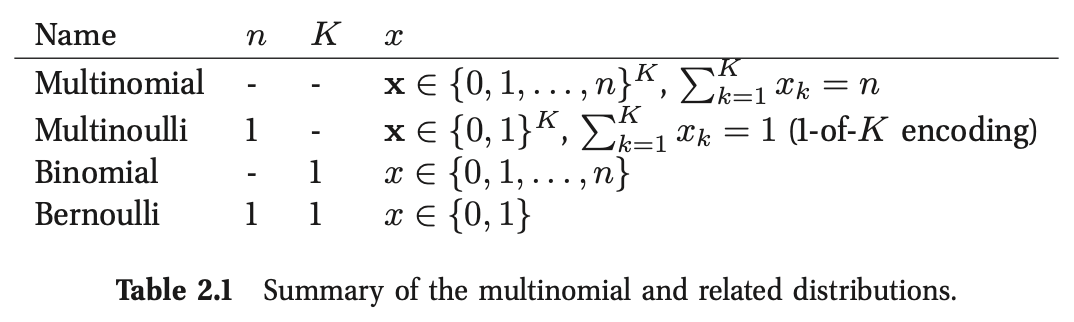
2.3.2.1 应用：DNA序列基序

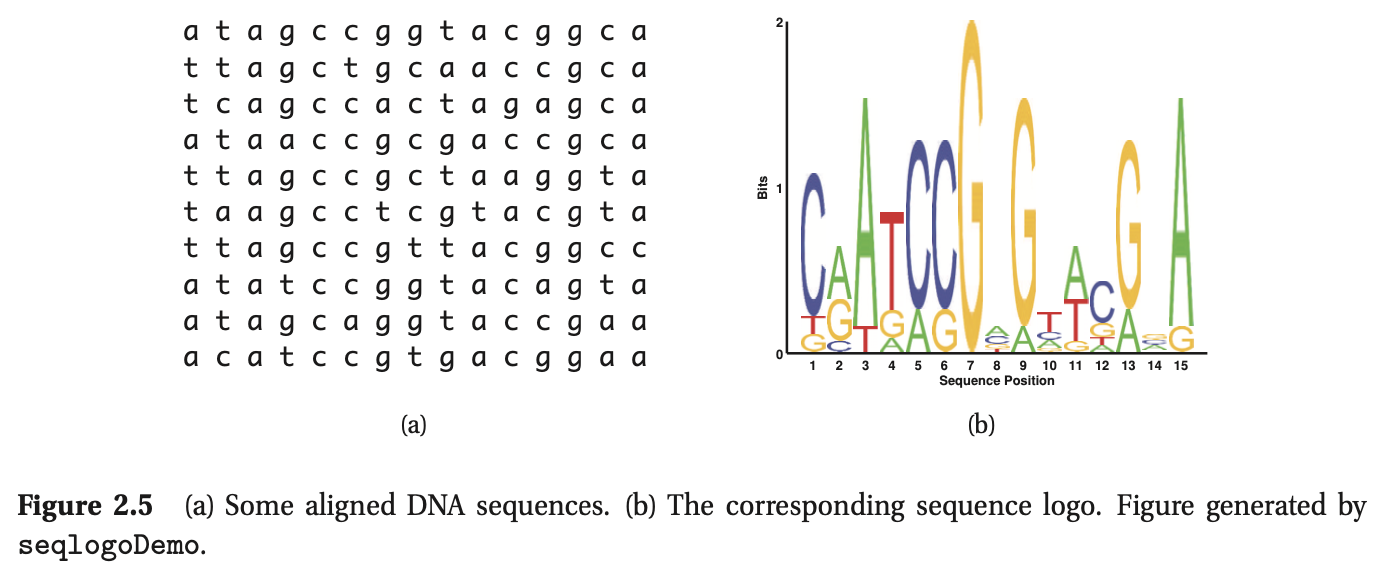
多项模型在生物序列分析中出现了一个有趣的应用。假设我们有一组(对齐的)DNA序列，如图2.5(a)所示，其中有10行(序列)和15列(沿基因组的位置)。我们看到几个位置是进化保守的(例如，因为它们是基因编码区域的一部分)，因为相应的列往往是“纯的”。例如，第13列都是G。

直观地总结数据的一种方法是使用序列标识(sequence logo):参见图2.5(b)。我们将字母A、C、G和T绘制成与它们的经验概率成比例的字体大小，并将最有可能的字母放在顶部。位置\(t\)的经验概率分布\(\hat{\boldsymbol{\theta}}_t\)，由计数向量归一化得到(见式2.38):

\[\begin{align} \mathbf{N}_t =& \left( \sum_{i=1}^N \mathbb{I}(X_{it}=1),\sum_{i=1}^N \mathbb{I}(X_{it}=2),\sum_{i=}^N \mathbb{I}(X_{it}=3),\sum_{i=1}^N \mathbb{I}(X_{it}=4) \right) \tag{2.37}\\ \hat{\boldsymbol{\theta}}_t =& \mathbf{N}_t/N &\tag{2.38} \end{align} \]

这种分布被称为基序。我们还可以计算每个位置上最可能出现的字母;这被称为共识序列。

2.3.3 泊松分布(Poisson distribution)

我们设\(X \in \{0,1,2,\ldots\}\)有一个参数为\(\lambda \gt 0\)的泊松分布，记为\(X \sim {\rm Poi}(\lambda)\)，其pmf为

\[{\rm Poi}(x|\lambda)=e^{-\lambda}\cfrac{\lambda^x}{x!} \tag{2.39} \]

第一项是归一化常数，用于确保分布和为1。泊松分布常被用作计算放射性衰变和交通事故等罕见事件的模型。部分图见图2.6。

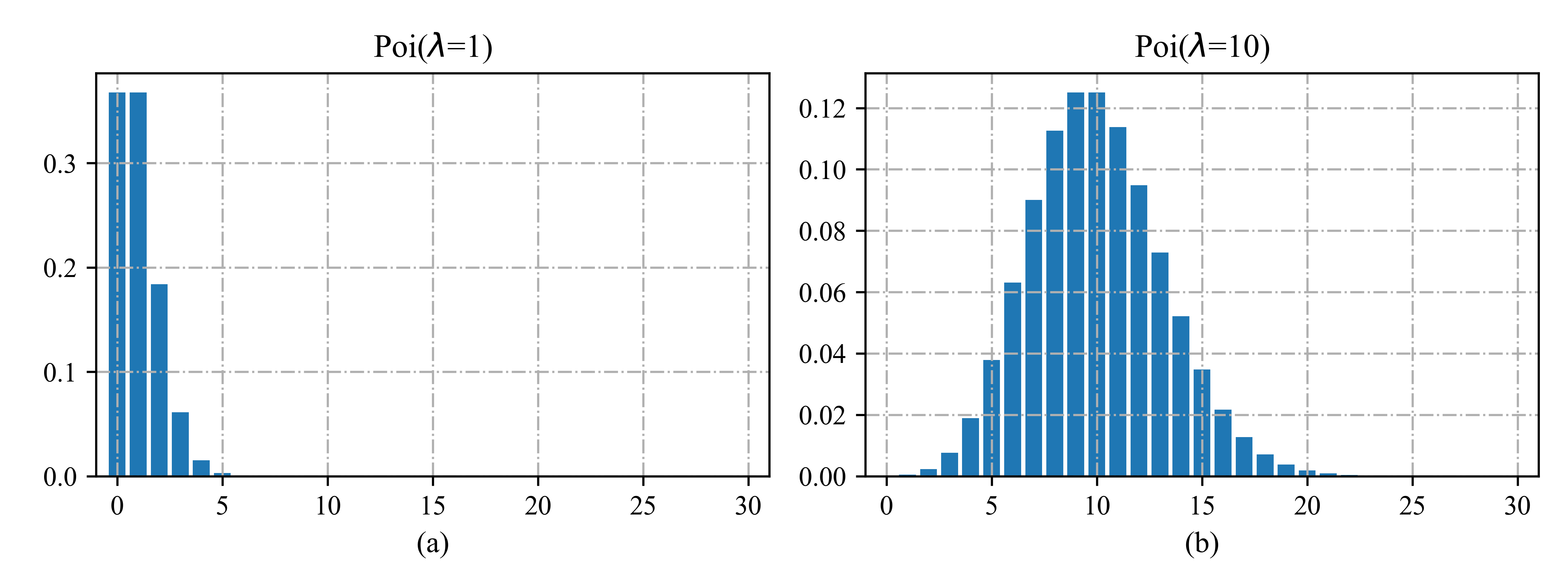
图2.6 \(\lambda \in \{1,10\}\)的一些泊松分布的图解。为了清晰起见，我们将x轴截短为25，但该分布对所有非负整数的支持。

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
plt.rc('font',family='Times New Roman')

lam=[1,10]
y1 = stats.poisson.pmf(np.arange(0,31,1),lam[0])
y2 = stats.poisson.pmf(np.arange(0,31,1),lam[1])

_,axes = plt.subplots(1,2,figsize=(8,3))
plt.sca(axes[0])
plt.bar(np.arange(0,31,1),y1)
plt.xlim([-1,31])
plt.xlabel("",fontsize=11)
plt.ylabel("",fontsize=11)
plt.tight_layout()
plt.grid(linestyle='-.')
plt.title(r'Poi($\lambda$=1)')
plt.xlabel('(a)')

plt.sca(axes[1])
plt.bar(np.arange(0,31,1),y2)
plt.xlim([-1,31])
plt.xlabel("",fontsize=11)
plt.ylabel("",fontsize=11)
plt.tight_layout()
plt.grid(linestyle='-.')
plt.title(r'Poi($\lambda$=10)')
plt.xlabel('(b)')

plt.savefig('./poissonPlotDemo.png',dpi=600)
plt.show()

2.3.4 经验分布(empirical distribution)

给定数据集，\(\mathcal{D}=\{x_1,\ldots,x_N\}\),我们定义为经验分布(empirical Distribution)，也叫做经验测量(empirical measure)，如下：

\[p_{emp}(A) \triangleq \cfrac{1}{N}\sum_{i=1}^{N}{\delta_{x_i}(A)} \tag{2.40} \]

其中，\(\delta_x(A)\)是狄利克雷测量(Dirac measure)，定义为

\[\delta_x(A) = \left\{ \begin{array}{l} 0 &{\rm if}\ x \notin A \\ 1 &{\rm if}\ x \in A \end{array} \right. \tag{2.41} \]

一般来说，我们可以将“权重”与每个样本相关联：

\[p(x)=\sum_{i=1}^Nw_i\delta_{x_i}(x) \tag{2.42} \]

这里我们要求\(0≤w_i≤1\)并且\(\sum_{i=1}^Nw_i =1\)。我们可以将其视为一个直方图，在数据点\(x_i\)处有“尖峰”，其中\(w_i\)决定尖峰\(i\)的高度。该分布将0概率分配给数据集中以外的任何点。

2.4 一些常用的连续分布

在本节中，我们将介绍一些常用的单变量(一维)连续概率分布。

2.4.1 高斯（正态）分布

统计学和机器学习中最广泛使用的分布是高斯分布(Gaussian distribution)或正态分布(normal distribution)。 它的pdf为

\[\mathcal{N}(x|\mu,\sigma^2) \triangleq \cfrac{1}{\sqrt{2\pi\sigma^2}}e^{-\cfrac{1}{2\sigma^2}(x-\mu)^2} \tag{2.43} \]

这里\(\mu=\mathbb{E}[X]\)是均值(mean)(和众数(mode))，\(\sigma^2 = {\rm var}[X]\)是方差。\(\sqrt{2\pi\sigma^2}\)是确保密度积分为1所需的归一常数。

我们用\(X∼\mathcal{N}(\mu,\sigma^2)\)表示\(p(X=x)=\mathcal{N}(x|\mu,\sigma^2)\)。如果\(X∼\mathcal{N}(0,1)\)，我们说\(X\)服从标准正态（standard normal）分布。图2.3(b)为该pdf的绘图，这有时被称为钟形曲线。

由于这是一个pdf，我们可以有\(p(x) > 1\)。为了看到这一点，考虑计算其中心的密度，\(x = μ\)。我们有\(\mathcal{N}(\mu|\mu,\sigma^2)=(\sigma\sqrt{2\pi})^{−1}e^0\)，所以如果\(\sigma<1/\sqrt{2\pi}\)，我们有\(p (x) > 1\)。

高斯的累积分布函数或cdf被定义为

\[\Phi(x;\mu,\sigma^2) \triangleq \int_{-\infty}^x{\mathcal{N}(z|\mu,\sigma^2)dz} \tag{2.44} \]

当\(μ = 0\)，\(σ^2 = 1\)时，此cdf的绘图见图2.3（a）。 这个积分没有闭合形式表达式，但内置在大多数软件包中。 特别是，我们可以根据错误函数（error function, erf）来计算它：

\[\Phi(x;\mu,\sigma) = \cfrac{1}{2}(1+\mathbf{erf}(z/\sqrt{2})) \tag{2.45} \]

其中 \(z=(x-\mu)/\sigma\)

\[\mathbf{erf}(x) \triangleq \cfrac{2}{\sqrt{\pi}}\int_{0}^{x}e^{-t^2}dt \tag{2.46} \]

高斯分布是统计学中应用最广泛的分布。首先，它有两个容易解释的参数，它们捕捉了分布的一些最基本的属性，即均值和方差。其次，中心极限定理(第2.6.3节)告诉我们，独立随机变量的和具有近似高斯分布，使其成为建模残差或“噪声”的好选择。第三，高斯分布做出最少的假设(具有最大的熵)，受到具有指定的均值和方差的约束，如我们在9.2.6节中所示；这使得它在许多情况下是一个很好的默认选择。最后，它有一个简单的数学形式，结果很容易实现，但通常是非常有效的方法，正如我们将看到的。见(Jaynes 2003，第7章)关于为什么高斯函数被如此广泛地使用的更广泛的讨论。

2.4.2 退化（Degenerate）pdf

在\(σ^2→0\)的极限下，高斯函数变成一个以\(μ\)为中心的无限高、无限薄的“spike”:

\[\lim_{\sigma^2 \rightarrow 0}\mathcal{N}(x|\mu,\sigma^2)=\delta(x-\mu) \tag{2.47} \]

其中\(\delta\)叫做狄利克雷delta函数(Dirac delta function)

\[\delta(x) = \left\{ \begin{array}{l} \infty & {\rm if} \ \ x=0\\ 0 & {\rm if} \ \ x \ne 0 \end{array} \right. \tag{2.48} \]

因此

\[\int_{-\infty}^{\infty} \delta(x)dx=1 \tag{2.49} \]

delta函数一个有用的属性是筛选属性(sifting property)，它从求和或积分中选择出单个项:

\[\int_{-\infty}^{\infty}f(x)\delta(x-\mu)dx=f(\mu) \tag{2.50} \]

因为被积函数只有在\(x−μ = 0\)时才非零。

高斯分布的一个问题是它对异常值很敏感，因为对数概率只随着距离中心的距离呈二次衰减。更稳健的分布是Student \(t\)分布，其pdf如下:

\[\tau(x|\mu,\sigma^2,\upsilon) \propto \left[1+\cfrac{1}{\upsilon}\left(\cfrac{x-\mu}{\sigma} \right)^2 \right]^{-\cfrac{\upsilon+1}{2}} \tag{2.51} \]

其中，\(\mu\)是均值，\(\sigma^2>0\)是尺度参数(scale parameter)，\(\upsilon>0\)叫做自由度(degrees of freedom)。部分图见图2.7。为了以后的参考，我们注意到分布具有以下属性:

\[{\rm mean}=\mu, \quad {\rm mode}=\mu, \quad {\rm var}=\cfrac{\upsilon\sigma^2}{(\upsilon-2)} \tag{2.52} \]

方差仅在\(ν > 2\)时才有定义。均值只有当\(ν > 1\)才有定义。

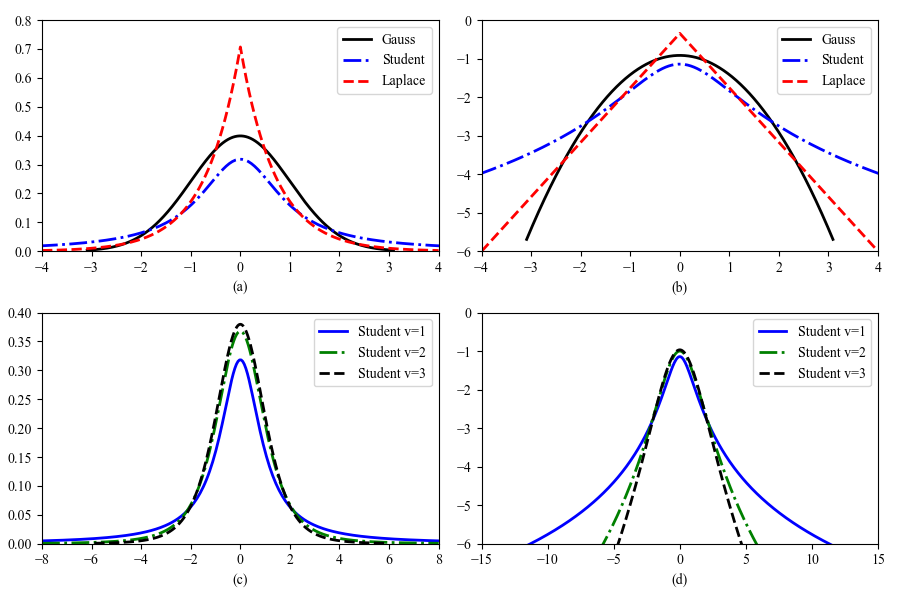
图2.7 (a) \(\mathcal{N}(0,1)\)， \(\mathcal{T}(0,1,1)\)和\({\rm Lap}(0,1/\sqrt{2})\)的pdf。高斯方程和拉普拉斯方程的均值是0，方差是1。当\(\upsilon=1\)时，Student的均值和方差未定义。(b)记录这些pdf文件。Student分布对于任何参数值都不是对数凹的，不像拉普拉斯分布总是对数凹的(和对数凸的…)，两者都是单峰的。

为了说明Student分布的稳健性，请查看图2.8。在左边，我们展示了一个高斯和一个学生适合一些没有异常值的数据。在右边，我们添加了一些异常值。我们看到高斯分布受到了很大的影响，而学生分布几乎没有变化。这是因为学生有更重的尾巴，至少对于小\(\upsilon\)(见图2.7)。

如果\(\upsilon = 1\)，这个分布被称为柯西(Cauchy)或洛伦兹(Lorentz)分布。值得注意的是，因为尾部很重，以至于定义均值的积分不收敛。

为了保证方差有限，我们要求\(\upsilon> 2\)。通常使用\(\upsilon = 4\)，它在一系列问题中表现良好(Lange et al. 1989)。对于\(\upsilon \gg 5\), Student分布迅速接近高斯分布，失去了鲁棒性。

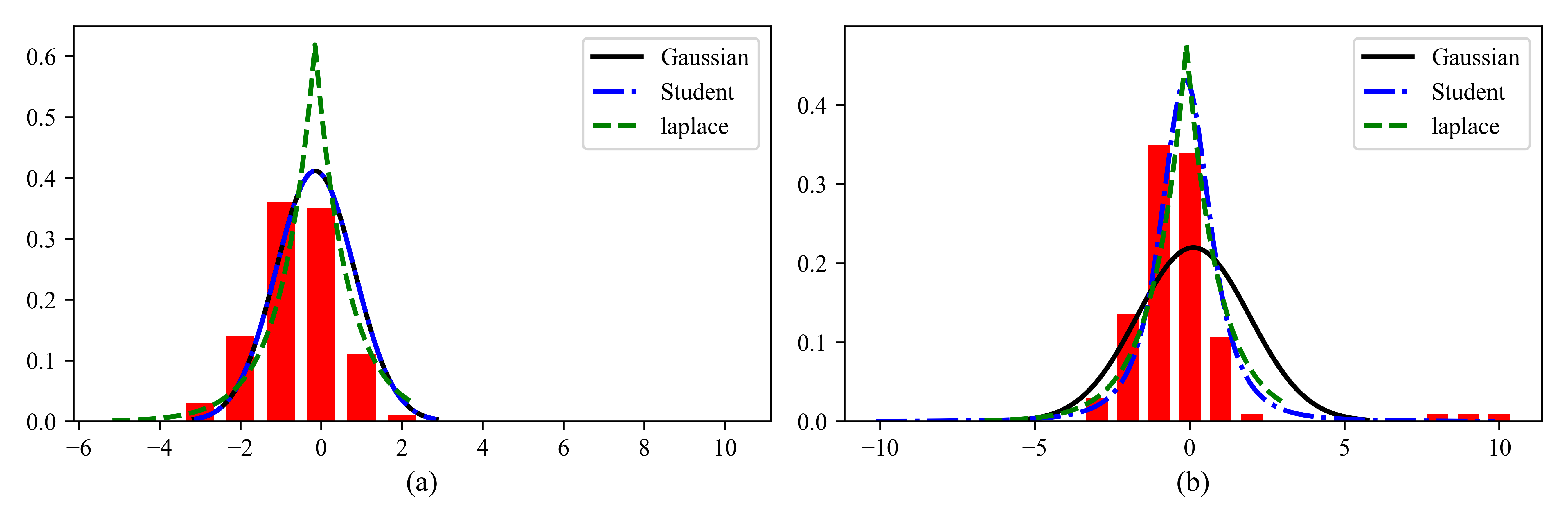
图2.8 解释异常值对拟合高斯分布、学生分布和拉普拉斯分布的影响。(a)没有异常值(outliers)(高斯曲线和学生曲线相互重叠)。(b)有异常值。我们看到高斯分布比学生分布和拉普拉斯分布更容易受到异常值的影响。

2.4.3 拉普拉斯分布

另一种具有重尾的分布是拉普拉斯分布(Laplace distribution)，也称为双面指数分布(double sided exponential distribution)。其有如下pdf：

\[{\rm Lap}(x|\mu, b) \triangleq \cfrac{1}{2b}exp\left(-\cfrac{|x-\mu|}{b} \right) \tag{2.53} \]

其中\(\mu\)是位置参数(location parameter)，\(b>0\)是尺度参数(scale parameter)，该分布具有以下属性：

\[{\rm mean}=\mu,\quad {\rm mode}=\mu,\quad {\rm var}=2b^2 \tag{2.54} \]

其对异常值的鲁棒性如图2.8所示。它在0处的概率密度大于高斯分布。这个属性是鼓励模型中的稀疏性的有用方法，我们将在13.3节中看到。

2.4.4 伽马分布

伽马分布(gamma distribution)对于正实数\(x>0\)随机变量是一个灵活的分布。它由两个参数定义，分别称为形状(shape)\(a > 0\)，速率(rate)\(b > 0\):

\[{\rm Ga}(T|\mathbf{shape}=a,\mathbf{rate}=b) \triangleq \cfrac{b^a}{\Gamma(a)}T^{a-1}e^{-Tb} \tag{2.55} \]

其中，\(\Gamma(a)\)是伽马函数(gamma function)：

\[\Gamma(x) \triangleq \int_{0}^{\infty}u^{x-1}e^{-u}du \tag{2.56} \]

部分图见图2.9。为了以后的参考，我们注意到分布具有以下属性:

\[{\rm mean}=\cfrac{a}{b}, \quad {\rm mode}=\cfrac{a-1}{b}, \quad {\rm var}=\cfrac{a}{b^2} \tag{2.57} \]

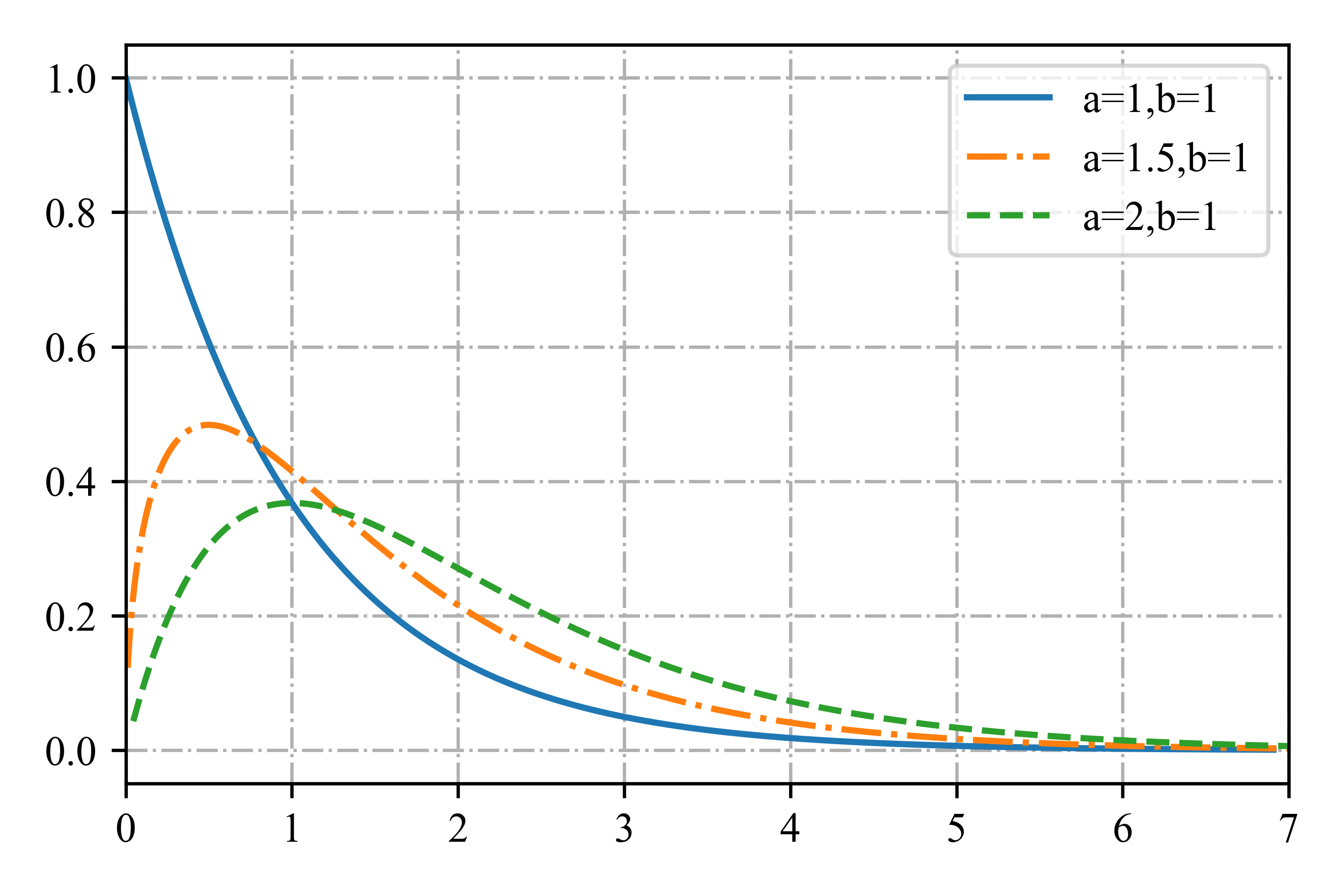
图2.9 部分Ga(a,b = 1)分布。如果a≤1，则众数为0，否则大于 0。当我们增加速率b时，我们减少了水平尺度，从而将所有东西向左和向上挤压。

有几种分布是伽马的特殊情况，我们在下面讨论。

• 指数分布(Exponential distribution)：定义为\({\rm Expon}(x|λ)\triangleq {\rm Ga}(x|1,λ)\)，其中\(λ\)为速率参数。这个分布描述了泊松过程中事件之间的时间间隔，即事件以恒定的平均速率\(λ\)连续独立地发生的过程。
• 爱尔朗分布(Erlang distribution)：当\(a\)是整数是，与伽马分布是一样的。通常固定\(a = 2\)，得到单参数Erlang分布，\({\rm Erlang}(x|λ) = {\rm Ga}(x|2,λ)\)，其中\(λ\)为速率参数。
• 卡方分布(Chi-squared distribution)： 定义为\(\chi^2(x|\upsilon) \triangleq {\rm Ga}(x|\frac{\upsilon}{2},\frac{1}{2})\)，这是平方高斯随机变量之和的分布。 更准确地说，如果\(Z_i ∼ \mathcal{N}(0,1)\)和\(S = \sum^ν_{i=1} Z_i^2\)，则\(S ∼ χ^2_ν\)。

另一个有用的结果如下：如果\(X∼{\rm Ga}(a,b)\)，那么可以证明\(\frac{1}{X}∼{\rm IG}(a,b)\)，其中\(\rm IG\)是逆伽玛(inverse gamma)分布

\[{\rm IG}(x|\mathbf{shape}=a,\mathbf{scale}=b) \triangleq \cfrac{b^a}{\Gamma(a)}x^{-(a+1)}e^{-b/x} \tag{2.58} \]

该分布具有这些属性：

\[{\rm mean}=\cfrac{b}{a-1},\quad {\rm mode}=\cfrac{b}{a+1},\quad {\rm var}=\cfrac{b^2}{(a-1)^2(a-2)} \tag{2.59} \]

只有当\(a>1\)时均值才存在，只有\(a>2\)时方差才存在。

2.4.5 贝塔分布

贝塔分布(beta distribution)支持区间\([0,1]\)，定义如下:

\[{\rm Beta}(x|a,b) = \cfrac{1}{B(a,b)}x^{a-1}(1-x)^{b-1} \tag{2.60} \]

这里\(B(a,b)\)是贝塔函数(beta function)，

\[B(a,b)\triangleq \cfrac{\Gamma(a)\Gamma{b}}{\Gamma(a+b)} \tag{2.61} \]

部分贝塔分布的分布图见图2.10。我们要求\(a,b > 0\)以确保分布是可积的(即确保\(B(a,b)\)存在)。如果\(a = b = 1\)，我们得到均匀分布，如果\(a\)和\(b\)均小于1，我们得到了一个双峰分布，在0和1处有“峰值”;如果a和b都大于1，则分布为单峰分布。为了便于以后参考，我们注意到该分布具有以下属性：

\[{\rm mean}=\cfrac{a}{a+b}, \quad {\rm mode}=\cfrac{a-1}{a+b-2}, \quad {\rm var}=\cfrac{ab}{(a+b)^2(a+b+1)} \tag{2.62} \]

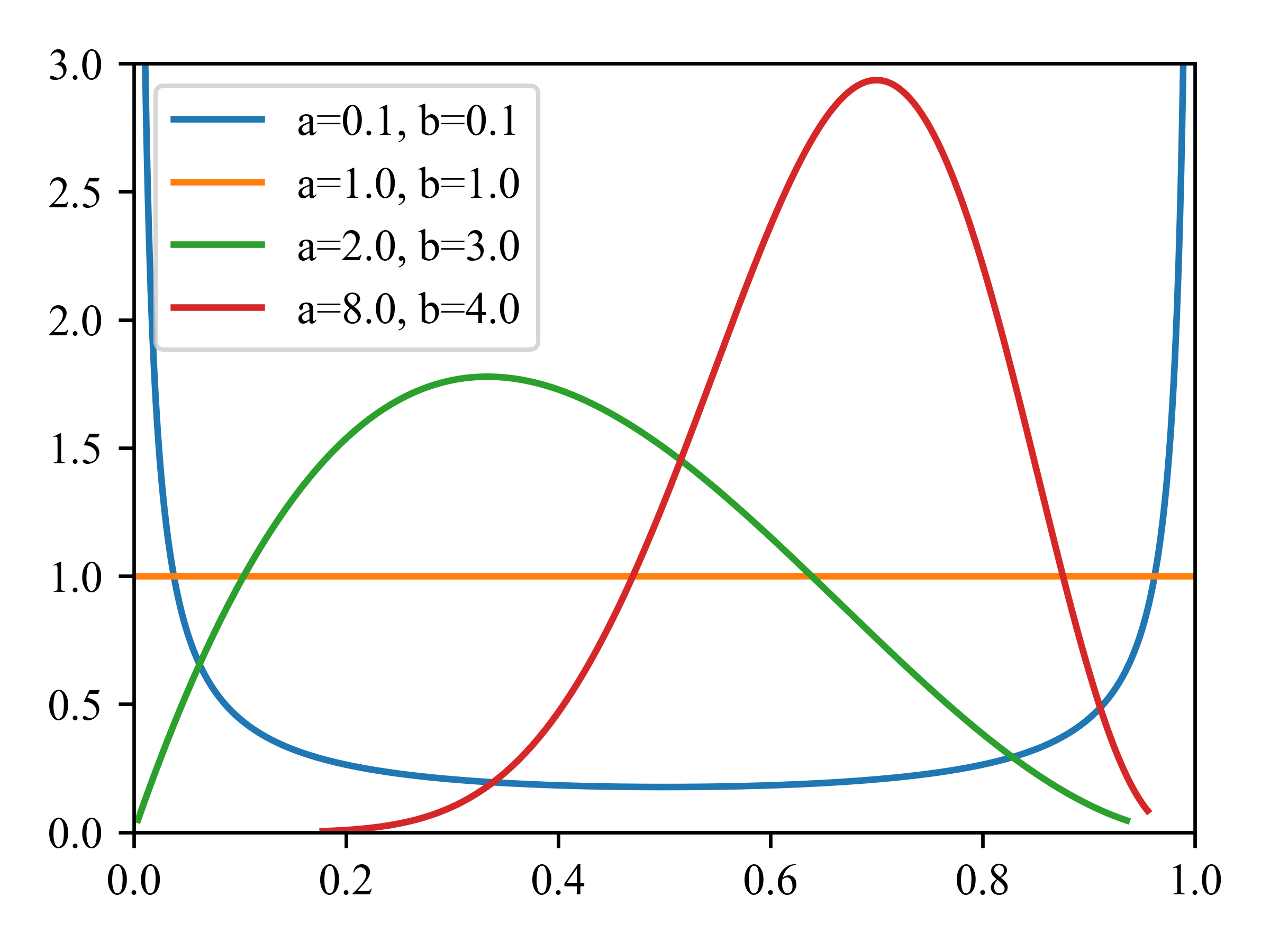
图2.10 一些beta分布。

from scipy.stats import beta
import matplotlib.pyplot as plt
import numpy as np

plt.rc('font', family='Times New Roman')

a=np.array([0.1, 1, 2, 8])
b=np.array([0.1, 1, 3, 4])

plt.subplots(1,1,figsize=(4,3))
for new_a, new_b in zip(a,b):
	print(new_a, new_b)
	x= np.linspace(beta.ppf(0.0001, new_a, new_b), beta.ppf(0.999, new_a, new_b),1000)
	plt.plot(x,beta.pdf(x, new_a, new_b), label='a={}, b={}'.format(new_a, new_b))

plt.xlim((0,1))
plt.ylim((0,3))
plt.legend()
plt.tight_layout()

plt.savefig('./betaPlotDemo.png',dpi=600)
plt.show()

2.4.6 帕累托分布

帕累托分布(Pareto distribution)用于模拟长尾(long tails)(也称为重尾(heavy tails))数量的分布。例如，据观察，英语中出现频率最高的单词(“the”)的出现频率大约是第二频繁单词(“of”)的两倍，而第二频繁单词(“of”)的出现频率是第四频繁单词的两倍，等等。如果我们把单词出现的频率和它们的排名画出来，我们就会得到一个幂律;这就是著名的齐普夫定律(Zipf's law)。财富的分配也同样不平衡，尤其是在美国这样的富豪国家。

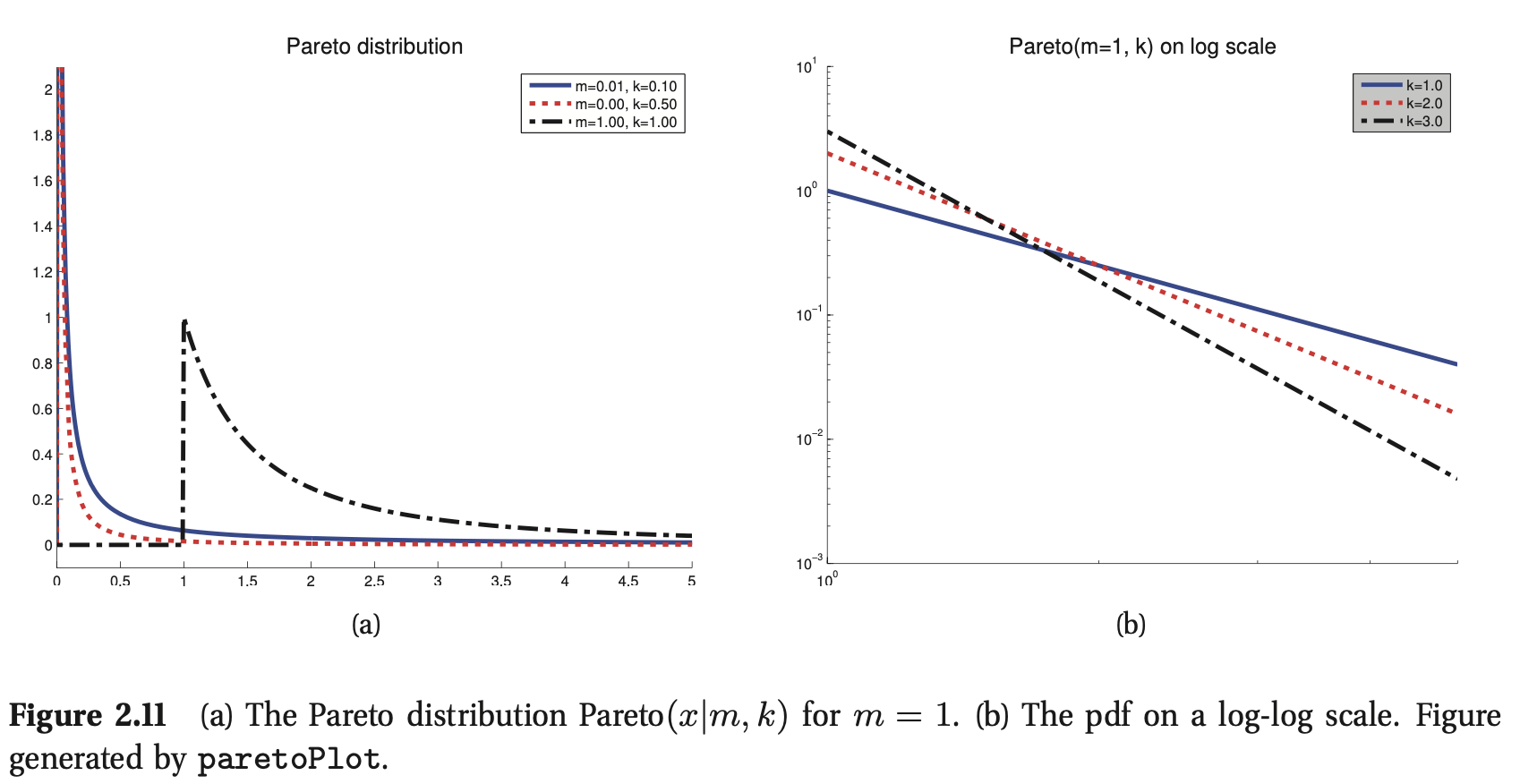
帕累托的pdf定义如下：

\[{\rm Pareto}(x|k,m)=km^kx^{-(k+1)}\mathbb{I}(x \geq m) \tag{2.63} \]

这个密度要求\(x\)必须大于某个常数\(m\)，但不能大太多，其中\(k\)控制什么是“太多”。当\(k→∞\)时，分布趋向于\(δ(x−m)\)，部分图如图2.11(a)所示。如果我们在对数尺度(log scale)上绘制分布，它会形成一条直线，对于某些常数\(a\)和\(c\)，它的形式为\(\log p(x)=a\log x+c\)。如图2.11(b)所示(这被称为幂律(power law))。该分布具有以下特性：

\[{\rm mean}=\cfrac{km}{k-1}\quad {\rm if}\ k>1,\quad {\rm mode}=m,\quad {\rm var}=\cfrac{m^2k}{(k-1)^2(k-2)} {\rm if}\ k>2 \tag{2.64} \]

2.5 联合概率分布

到目前为止，我们主要集中在建模单变量概率分布。在本节中，我们开始讨论更具挑战性的问题，即在多个相关随机变量上构建联合概率分布;这将是本书的中心话题。

对于一组\(D > 1\)变量，联合概率分布的形式为\(p(x_1,\ldots,x_D)\)，并对变量之间的(随机)关系进行建模。如果所有变量都是离散的，我们可以将联合分布表示为一个大的多维数组，每个维度有一个变量。然而，定义这样一个模型所需的参数数量是\(O(K^D)\)，其中\(K\)是每个变量的状态数。

我们可以用更少的参数来定义高维联合分布，通过做条件独立性假设，正如我们在第10章中解释的那样。在连续发布的情况下，另一种方法是将pdf的形式限制为某些函数形式，其中一些我们将在下面讨论。

2.5.1 协方差和相关系数

两个随机变量\(X\)和\(Y\)之间的协方差(covariance)度量了X和Y(线性)相关的程度。协方差定义为

\[{\rm cov}[X,Y] \triangleq \mathbb{E}[(x-\mathbb{E}(X))(Y-\mathbb{E}(Y))]=\mathbb{E}[XY]-\mathbb{E}[X]\mathbb{E}[Y] \tag{2.65} \]

如果\(\mathbf{x}\)是一个\(d\)维随机向量，其协方差矩阵(covariance matrix)定义为如下对称正定矩阵(symmetric, positive definite matrix):

\[\begin{align} {\rm cov}[{\mathbf x}] &\triangleq \mathbb{E}\left[({\mathbf x}-\mathbb{E}[{\mathbf x}])({\mathbf x}-\mathbb{E}[{\mathbf x}])^T \right] \tag{2.66} \\ &= \left( \begin{array}{c} &{\rm var}[X_1]& \quad &{\rm cov}[X_1,X_2]& \quad &\cdots& \quad &{\rm cov}[X_1,X_d]& \\ &{\rm cov}[X_2,X_1]& \quad &{\rm var}[X_2]& \quad &\cdots& \quad &{\rm cov}[X_2,X_d]& \\ &\vdots& \quad &\vdots& \quad &\ddots& \quad &\vdots& \\ &{\rm cov}[X_d,X_1]& \quad &{\rm cov}[X_d,X_2]& \quad &\cdots& \quad &{\rm var}[X_d]& \\ \end{array} \right) \tag{2.67} \end{align} \]

协方差可以在0到无穷大之间。有时，使用具有有限上界的标准化度量更方便。\(X\)和\(Y\)之间的Pearson相关系数(correlation coefficient)定义为

\[{\rm corr}[X,Y] \triangleq \cfrac{{\rm cov}[X,Y]}{\sqrt{{\rm var}[X]{\rm var}[Y]}} \tag{2.68} \]

相关矩阵(correlation matrix)的形式是

\[{\mathbf R} = \left( \begin{array}{c} &{\rm corr}[X_1,X_1] \quad &{\rm corr}[X_1,X_2] \quad &\cdots &{\rm corr}[X_1,X_d] \\ &\vdots \quad &\vdots \quad &\ddots \quad &\vdots \\ &{\rm corr}[X_d,X_1] \quad &{\rm corr}[X_d,X_2] \quad &\cdots \quad &{\rm corr}[X_d,X_d] \\ \end{array} \right) \tag{2.69} \]

我们可以证明\(−1≤{\rm corr} [X, Y]≤1\)。因此，在相关矩阵中，对角线上的每个元素都是1，其他元素在-1到1之间。

对于某些参数\(a\)和\(b\)，当且仅当\(Y = aX +b\)，即\(X\)和\(Y\)之间存在线性关系时，也可以证明\({\rm corr}[X,Y] = 1\)。直观上，人们可能会认为相关系数与回归线的斜率有关，即表达式\(Y = aX + b\)中的系数\(a\)。然而，正如我们在后面的公式7.99中所示，回归系数实际上由\(a = {\rm cov }[X, Y] /{\rm var}[X]\)给出。考虑相关系数的一个更好的方法是作为一个线性度:见图2.12。

如果\(X\)和\(Y\)是独立的，即\(p(X, Y) = p(X)p(Y)\)，则\({\rm cov} [X, Y] = 0\)，因此\({\rm corr} [X, Y] = 0\)，因此它们是不相关的。然而，相反的情况并非如此：不相关并不意味着独立。例如，设\(X∼U(−1,1)\)，\(Y = X^2\)。显然\(Y\)依赖于\(X\)(事实上，\(Y\)是由\(X\)唯一决定的)，然而我们可以证明\({\rm corr} [X, Y] = 0\)。图2.12显示了这一事实的一些显著例子。这显示了几个数据集，其中X和Y之间有明显的依赖关系，但相关系数为0。随机变量之间依赖关系的更一般的度量是互信息mutual information，只有当变量相互独立时，这个才为0。

2.5.2 多元高斯

多元高斯 multivariate Gaussian函数或多元正态 multivariate normal函数(MVN)是应用最广泛的连续变量联合概率密度函数。我们在第4章详细讨论了MVN；这里我们只给出一些定义和图表。

\(D\)维MVN上的pdf定义如下:

\[\begin{align*} \mathcal{N}({\mathbf x}|{\boldsymbol \mu}, \boldsymbol{\Sigma}) \triangleq \cfrac{1}{(2\pi)^{D/2}|\boldsymbol{\Sigma}|^{1/2}} {\rm exp}\left[ \cfrac{1}{2}({\mathbf x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1}({\mathbf x}-\boldsymbol{\mu}) \right] \tag{2.70} \end{align*} \]

其中\(\boldsymbol{\mu} = \mathbb{E}[\mathbf{x}] \in \mathbb{R}^D\)为均值向量，\(\boldsymbol{\Sigma} = {\rm cov}[\mathbf{x}]\)为\(D × D\)协方差矩阵。有时我们会用精度矩阵 precision matrix或浓度矩阵 concentration matrix来代替。这就是协方差逆矩阵，\(\boldsymbol{\Lambda} = \boldsymbol{\Sigma}^{−1}\)。归一化常数\((2\pi)^{−D/2}|\boldsymbol{\Lambda}|^{1/2}\)只是确保pdf积分为1。

图2.13在2d中绘制了三种不同协方差矩阵的一些MVN密度。一个完整的协方差矩阵有\(D(D + 1)/2\)个参数(我们除以2，因为\(\boldsymbol \Sigma\)是对称的)。对角协方差矩阵有\(D\)个参数，非对角项为0。球面spherical或各向同性isotropic协方差\(\boldsymbol\Sigma=\sigma^2 \mathbf{I}_D\)有一个自由参数。

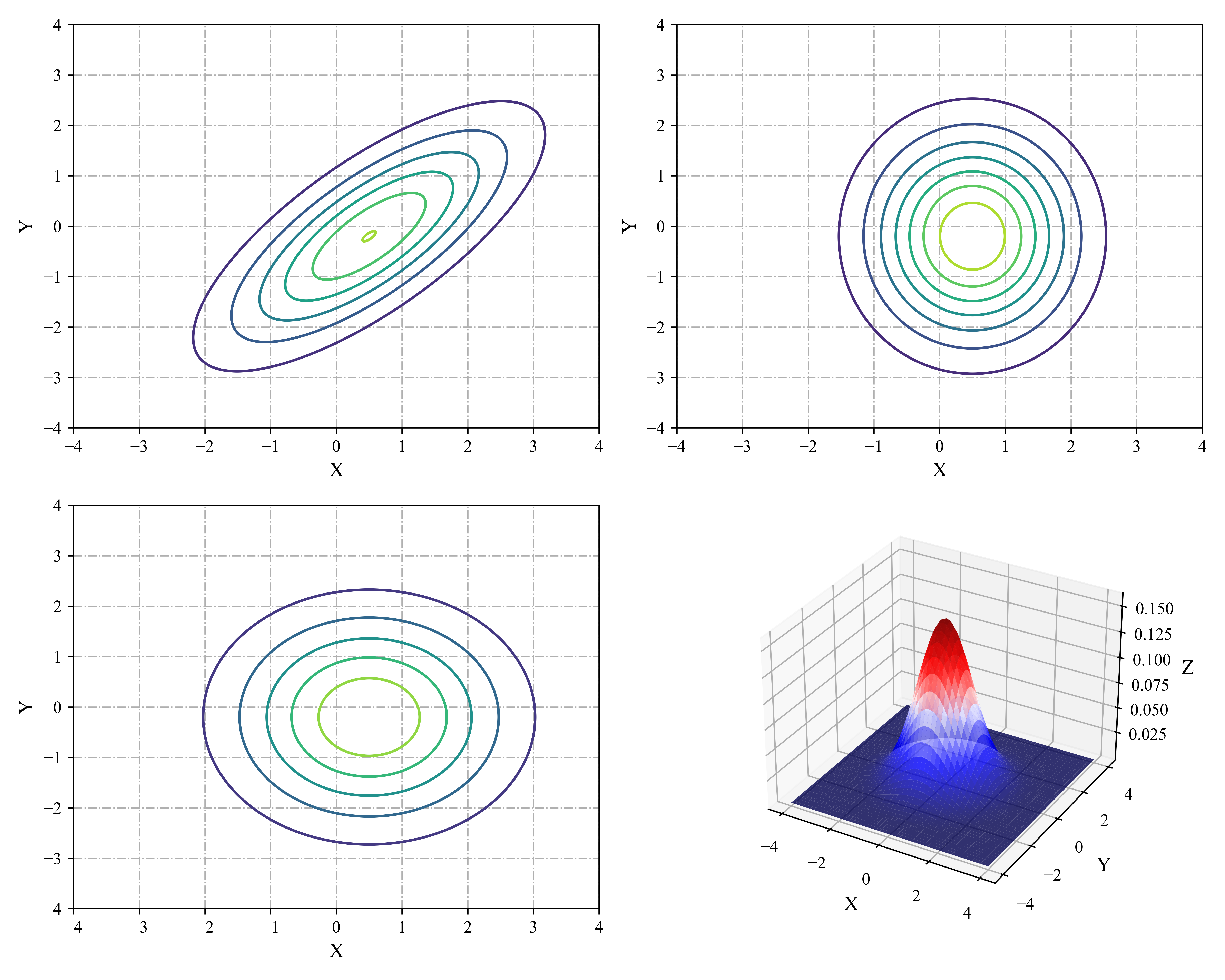
图2.13 我们展示二维高斯的水平集。（a）一个完整的协方差具有椭圆轮廓。（b）对角协方差举证是轴对齐椭圆。（c）球形协方差矩阵具有圆形。（d）球形高斯c的表面图。

import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
import numpy as np

plt.rc('font',family='Times New Roman')

x,y = np.meshgrid(np.linspace(-4,4,1000), np.linspace(-4,4,1000))
d=np.dstack([x,y])
rv1= multivariate_normal(mean=[0.5,-0.2], cov=[[2,1.5],[1.5,2]])
rv2 = multivariate_normal([0.5,-0.2],[[1,0],[0,1.8]])
rv3 = multivariate_normal([0.5,-0.2],[[1.8,0],[0,1.8]])
rv4 = multivariate_normal([0,0],[[1,0],[0,1]])

fig = plt.figure(figsize=(10, 8), facecolor='w')

ax1 = fig.add_subplot(221)
ax1.set_xlabel("X", fontsize=12)
ax1.set_ylabel("Y", fontsize=12)
ax1.contour(x, y, rv1.pdf(d),  alpha =1.0, zorder=10)
ax1.grid(linestyle='-.')

ax2 = fig.add_subplot(222)
ax2.set_xlabel("X", fontsize=12)
ax2.set_ylabel("Y", fontsize=12)
ax2.contour(x, y, rv2.pdf(d),  alpha =1.0, zorder=10)
ax2.grid(linestyle='-.')

ax3 = fig.add_subplot(223)
ax3.set_xlabel("X", fontsize=12)
ax3.set_ylabel("Y", fontsize=12)
ax3.contour(x, y, rv3.pdf(d),  alpha =1.0, zorder=10)
ax3.grid(linestyle='-.')

ax4 = fig.add_subplot(224,projection='3d')
ax4.plot_surface(x,y,rv4.pdf(d),cmap='seismic', alpha=0.8)
ax4.set_xlabel("X", fontsize=12)
ax4.set_ylabel("Y", fontsize=12)
ax4.set_zlabel("Z", fontsize=12)
ax4.grid(linestyle='-.')

plt.tight_layout()
plt.savefig('./gaussPlot2Ddemo.png',dpi=600)
plt.show()

2.5.3 多元学生t分布

MVN的一个更稳健robust的替代方法是多元学生tmultivariate Student t分布，pdf为：

\[\begin{align*} \tau({\mathbf x}|\boldsymbol{\mu},\boldsymbol{\Sigma},\nu) &= \cfrac{\Gamma(\nu/2+D/2)}{\Gamma(\nu/2)}\cfrac{|\boldsymbol{\Sigma}|^{-1/2}}{\nu^{D/2}\pi^{D/2}}\times \left[ 1+\cfrac{1}{\nu}(\mathbf{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})\right]^{-(\cfrac{\nu+D}{2})} \tag{2.71}\\ &= \cfrac{\Gamma(\nu/2+D/2)}{\Gamma(\nu/2)} |\pi\mathbf{V}|^{-1/2} \times \left[ 1+\cfrac{1}{\nu}(\mathbf{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})\right]^{-(\cfrac{\nu+D}{2})} \tag{2.72} \end{align*} \]

其中\(\boldsymbol{\Sigma}\)被称为尺度矩阵scale matrix(因为它不是协方差矩阵)，\(\mathbf{V} = \nu\boldsymbol{\Sigma}\)。这个函数的尾部比高斯函数的尾部大。\(\nu\)越小，尾巴就越胖。当\(\nu \rightarrow \infty\)时，分布趋近于高斯分布。该分布具有以下属性：

\[{\rm mean}=\boldsymbol{\mu},\quad {\rm mode}=\boldsymbol{\mu},\quad {\rm Cov}=\cfrac{\nu}{\nu-2}\boldsymbol{\Sigma} \tag{2.73} \]

2.5.4 狄利克雷分布

beta分布的多元变量推广是狄利克雷分布Dirichlet distribution，它支持概率单纯形probability simplex，定义如下：

\[S_K = \left \{{\mathbf x}: 0\le x_k \le 1, \sum_{k=1}^Kx_k=1\right\} \tag{2.74} \]

pdf定义如下：

\[{\rm Dir}({\mathbf x}|\boldsymbol{\alpha}) \triangleq \cfrac{1}{B(\boldsymbol{\alpha})}\prod_{k=1}^{K}x_k^{\alpha_k-1}\mathbb{I}(x \in S_K) \tag{2.75} \]

其中\(B(\alpha_1,\ldots,\alpha_K)\)是beta函数对\(K\)个变量的自然推广：

\[B(\boldsymbol{\alpha}) \triangleq \cfrac{\prod_{k=1}^{K}\Gamma(\alpha_k)}{\Gamma(\alpha_0)} \tag{2.76} \]

其中：\(\alpha_0 \triangleq \sum_{k=1}^{K} \alpha_k\)

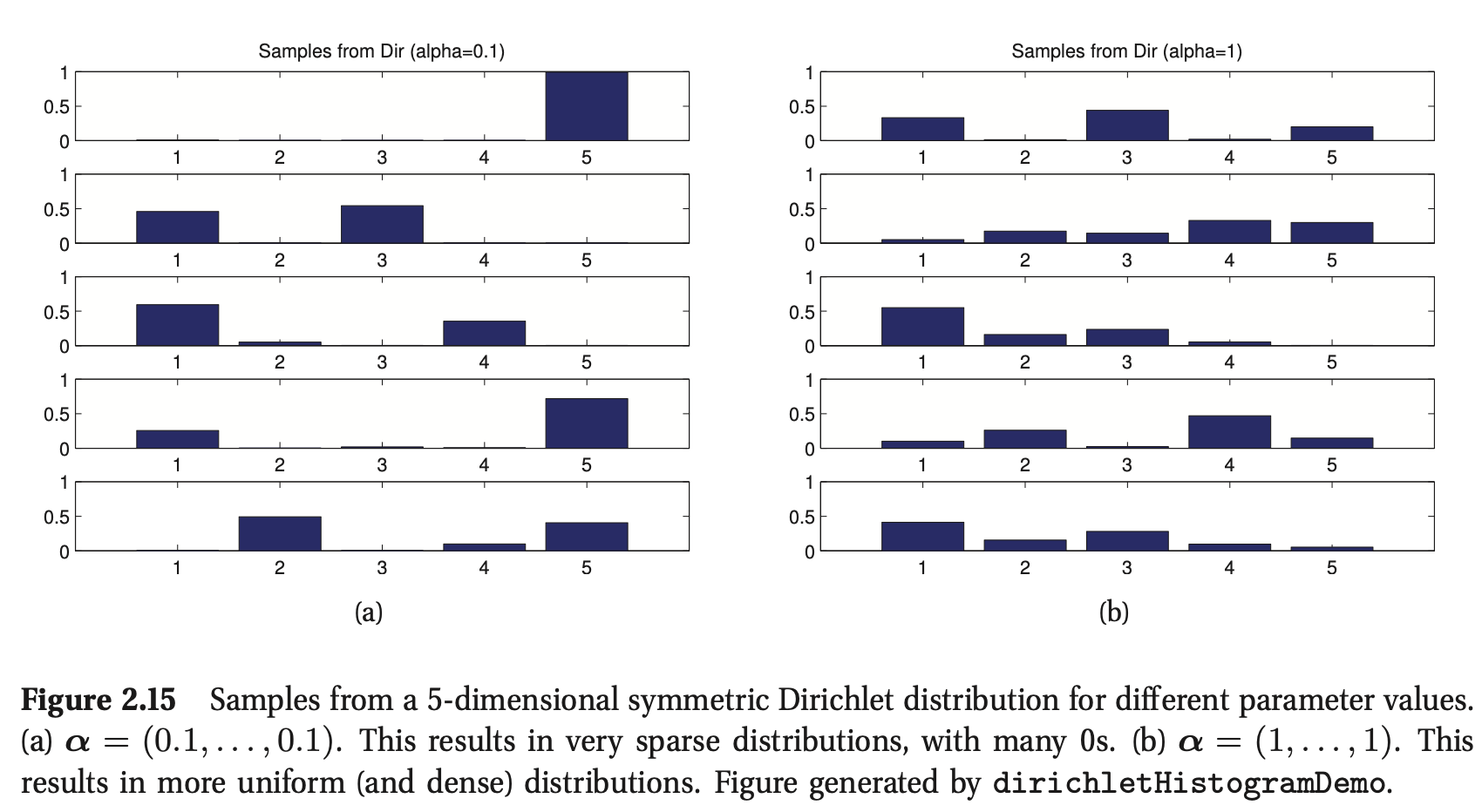
图2.14显示了\(K = 3\)时的Dirichlet，图2.15为一些抽样概率向量。我们看到\(α_0=\sum^K_{k=1}α_k\)控制着分布的强度(峰值是多少)，\(α_k\)控制着峰值出现的位置。例如，\({\rm Dir}(1,1,1)\)是均匀分布，\({\rm Dir}(2,2,2)\)是宽分布，中心在\((1/3,1/3,1/3)\)，\({\rm Dir}(20,20,20)\)是窄分布，中心在(1/3,1/3,1/3)。如果所有的\(k\)都是\(α_k < 1\)，我们会在单形的角处得到“尖峰”。

import numpy as np
from scipy.stats import dirichlet
import matplotlib.pyplot as plt
import matplotlib.tri as mtri
import math
from math import gamma
from operator import mul

plt.rc('font', family='Times New Roman')

# 在我们的等边三角形上生成一组笛卡尔坐标
corners = np.array([[0,0],[1,0],[0.5,0.75**0.5]])
area = 0.5*1*0.75**0.5
triangle = mtri.Triangulation(corners[:,0],corners[:,1])

# For each corner of the triangle, the pair of other corners
pairs = [corners[np.roll(range(3), -i)[1:]] for i in range(3)]
# The area of the triangle formed by point xy and another pair or points
tri_area = lambda xy, pair: 0.5 * np.linalg.norm(np.cross(*(pair - xy)))

def xy2bc(xy, tol=1.e-4):
    '''Converts 2D Cartesian coordinates to barycentric.'''
    coords = np.array([tri_area(xy, p) for p in pairs]) / area
    return np.clip(coords, tol, 1.0 - tol)
    
class Dirichlet(object):
    def __init__(self, alpha):
        self._alpha = np.array(alpha)
        self._coef = gamma(np.sum(self._alpha)) / np.multiply.reduce([gamma(a) for a in self._alpha])
    def pdf(self, x):
        '''Returns pdf value for `x`.'''
        from operator import mul
        return self._coef * np.multiply.reduce([xx ** (aa - 1) for (xx, aa)in zip(x, self._alpha)])

def draw_pdf_contours(dist, nlevels=200, subdiv=8, **kwargs):
    refiner = mtri.UniformTriRefiner(triangle)
    trimesh = refiner.refine_triangulation(subdiv=subdiv)
    pvals = [dist.pdf(xy2bc(xy)) for xy in zip(trimesh.x, trimesh.y)]
    plt.tricontourf(trimesh, pvals, nlevels, cmap='jet', **kwargs)
    plt.axis('equal')
    plt.xlim(0, 1)
    plt.ylim(0, 0.75**0.5)
    plt.axis('off')

draw_pdf_contours(Dirichlet([20, 2, 2]))

plt.savefig('./dirichlet3dPlot(c).png', dpi=600)
plt.show()

为了将来参考，该分布具有以下属性：

\[\mathbb{E}[x_k]=\cfrac{\alpha_k}{\alpha_0},\quad {\rm mode}[x_k]=\cfrac{\alpha_k-1}{\alpha_0-K},\quad {\rm var}[x_k]=\cfrac{\alpha_k(\alpha_0-\alpha_k)}{\alpha_0^2(\alpha_0+1)} \tag{2.77} \]

其中，\(\alpha_0=\sum_k{\alpha_k}\)，我们经常使用对称狄利克雷先验，形式为\(α_k=α/K\)。在这种情况下，均值变为\(1/K\)，方差变为\({\rm var} [x]=\frac{K-1}{K^2(\alpha+1)}\)。因此，增加\(α\)会增加分布的精度(减少方差)。

2.6 随机变量的变换

如果\(x ∼ p()\)是某个随机变量，而\({\mathbf y} = f({\mathbf x})\)，那么\({\mathbf y}\)的分布是什么？ 这是我们在本节中讨论的问题。

2.6.1 线形变换

假定\(f()\)是线性函数：

\[{\mathbf y} = f({\mathbf x})=\mathbf{AX+b} \tag{2.78} \]

这种情况下，我们可以容易的推导出\({\mathbf{y}}\)的均值和方差。首先均值如下：

\[\mathbb{E}[\mathbf{y}] = \mathbb{E}[\mathbf{Ax+b}]=\mathbf{A}\boldsymbol{\mu}+\mathbf{b} \tag{2.79} \]

其中\(\boldsymbol{\mu}=\mathbb{E}[\mathbf{x}]\)，这叫做线性期望linearity of expectation。如果\(f()\)是标量函数scalar-valued function，\(f(\mathbf{x})=\mathbf{a}^T\mathbf{x}+b\)，相应的结果是：

\[\mathbb{E}[\mathbf{a}^T\mathbf{x}+b] = \mathbf{a}^T\boldsymbol{\mu}+b \tag{2.80} \]

对于协方差，我们有：

\[{\rm cov}[\mathbf{y}]={\rm cov}[\mathbf{Ax+b}]=\mathbf{A}\boldsymbol{\Sigma}\mathbf{A} \tag{2.81} \]

其中，\(\boldsymbol{\Sigma}={\rm cov}[\mathbf{x}]\)。如果\(f()\)是标量值scalar valued，结果为：

\[{\rm var}[y]={\rm var}[\mathbf{a}^T\mathbf{x}+b]=\mathbf{a}^T\boldsymbol{\Sigma} \mathbf{a} \tag{2.82} \]

我们将在后面的章节中广泛地使用这两个结果。然而，请注意，只有当\(\mathbf{x}\)是高斯分布时，均值和协方差才完全定义\(\mathbf{y}\)的分布。一般来说，我们必须使用下面描述的技术来推导\(\mathbf{y}\)的完整分布，而不仅仅是它的前两个时刻。

2.6.2 生成变换

如果\(X\)是一个离散的随机变量，我们可以通过简单地将\(f(x) = y\)的所有\(x\)的概率质量probability mass相加来推导出\(y\)的pmf:

\[p_y(y)=\sum_{x:f(x)=y}p_x(x) \tag{2.83} \]

例如，如果\(X\)为偶数，\(f(X) = 1\)，否则\(f(X)=0\)，且\(p_x(X)\)在集合\(\{1,…, 10\}\)，那么\(p_y(1)=\sum_{x \in \{2、4、6、8、10\}}p_x(x)=0.5\)，\(p_y(0) = 0.5\)。注意，在这个例子中，\(f\)是一个多对一many-to-one函数。

如果\(X\)是连续的，我们不能使用公式2.83，因为\(p_x(X)\)是一个密度，而不是pmf，我们不能对密度求和。相反，我们使用cdf：

\[P_y(y) \triangleq P(Y \leq y) = P(f(X) \leq y) = P(X \in \{ x| f(x) \leq y \}) \tag{2.84} \]

我们可以通过对cdf微分推导出\(y\)的pdf。

在单调函数的情况下是可逆函数，我们可以写：

\[P_y(y) = P(f(x)\leq y)= P(X \leq f^{-1}(y))=P_x(f^{-1}(y)) \tag{2.85} \]

求导数得到：

\[p_y(y)\triangleq \cfrac{d}{dy}P_y(y)=\cfrac{d}{dy}P_x(f^{-1}(y))=\cfrac{dx}{dy}\cfrac{d}{dx}P_x(x) =\cfrac{dx}{dy}p_x(x) \tag{2.86} \]

其中\(x=f^{-1}(y)\)，我们可以把\(dx\)看成\(x\)空间中体积的单位；类似地，\(dy\)测量\(y\)空间中的体积单位。因此\(\frac{dx}{dy}\)表示体积的变化。由于\(dy\)变化的符号不重要，我们取绝对值得到一般表达式:

\[p_y(y)=p_x(x)\left |\cfrac{dx}{dy} \right | \tag{2.87} \]

这叫做变量变换change of variables公式。我们可以更直观地理解这个结果。\((x,x + δx)\)范围内的观测值将转换为\((y, y + δy)\)，其中\(p_x(x)δx≈p_y(y)δy\)。因此，\(p_y(y) \approx p_x(x)\left |\cfrac{dx}{dy} \right |\)。例如，假定\(X \sim U(-1,1)\)，\(Y=X^2\)。那么，\(p_y(y)=\frac{1}{2}y^{-\frac{1}{2}}\)。

2.6.2.1 多元变量变换*

我们可以将先前的结果扩展到多元分布，如下所示。设\(f\)是一个将\(\mathbb{R}^n\)映射到\(\mathbb{R}^n\)的函数，令\(\mathbf{y} = f(\mathbf{x})\)那么它的雅可比矩阵J Jacobian matrix J为：

\[\mathbf{J_{x \rightarrow y}} \triangleq \cfrac{\partial(y_1,\ldots,y_n)}{\partial(x_1,\ldots,x_n)} \triangleq \left( \begin{array}{c} \cfrac{\partial y_1}{\partial x_1} &\quad& \ldots &\quad& \cfrac{\partial y_1}{\partial x_n} \\ \vdots &\quad& \ddots &\quad& \vdots \\ \cfrac{\partial y_n}{\partial x_1} & \quad & \ldots &\quad& \cfrac{\partial y_n}{\partial x_n} \\ \end{array} \right) \tag{2.88} \]

\(|{\rm det}\ \mathbf{J}|\)测量当我们施加\(f\)时，一个单位立方体的体积变化。

如果\(f\)是一个可逆映射，我们可以使用逆映射\(\mathbf{y→x}\)的雅可比矩阵定义转换变量的pdf：

\[p_y(\mathbf{y})=p_x({\mathbf{x}})\left| {\rm det}(\cfrac{\partial \mathbf{x}}{\partial \mathbf{y}}) \right| =p_x(\mathbf{x})|{\rm det}\ \mathbf{J}_\mathbf{y \rightarrow x}| \tag{2.89} \]

举个简单的例子，考虑将密度从笛卡尔坐标Cartesian coordinates\(\mathbf{x} = (x_1, x_2)\)转换到极坐标polar coordinates\(\mathbf{y}= (r，θ)\)，其中\(x_1 = r\cosθ\)， \(x_2 = r\sinθ\)。然后：

\[\mathbf{J_{y \rightarrow x}} = \left( \begin{array}{c} \cfrac{\partial x_1}{\partial r} &\ \cfrac{\partial x_1}{\partial \theta}\\ \cfrac{\partial x_2}{\partial r} &\ \cfrac{\partial x_2}{\partial \theta} \end{array} \right) =\left( \begin{array}{c} \cos\theta &\ -r\sin\theta \\ \sin\theta &\ r\cos\theta \end{array} \right) \tag{2.90} \]

同时：

\[|{\rm det}\ \mathbf{J}| = |r\cos^2 \theta+r\sin^2\theta|=|r| \tag{2.91} \]

因此：

\[p_{\mathbf{y}}(\mathbf{y})=p_{\mathbf{x}}(\mathbf{x})|{\rm det} \ \mathbf{J}| \tag{2.92} \]

\[p_{r,\theta}=p_{x_1,x_2}(x_1,x_2)r=p_{x_1,x_2}(r\cos\theta,r\sin\theta)r \tag{2.93} \]

要从几何上看这一点，请注意图2.16中阴影补丁的面积由

\[P(r\leq R\leq r+dr,\theta \leq \Theta \leq \theta+d\theta) = p_{r,\theta}(r,\theta)dr\ d\theta \tag{2.94} \]

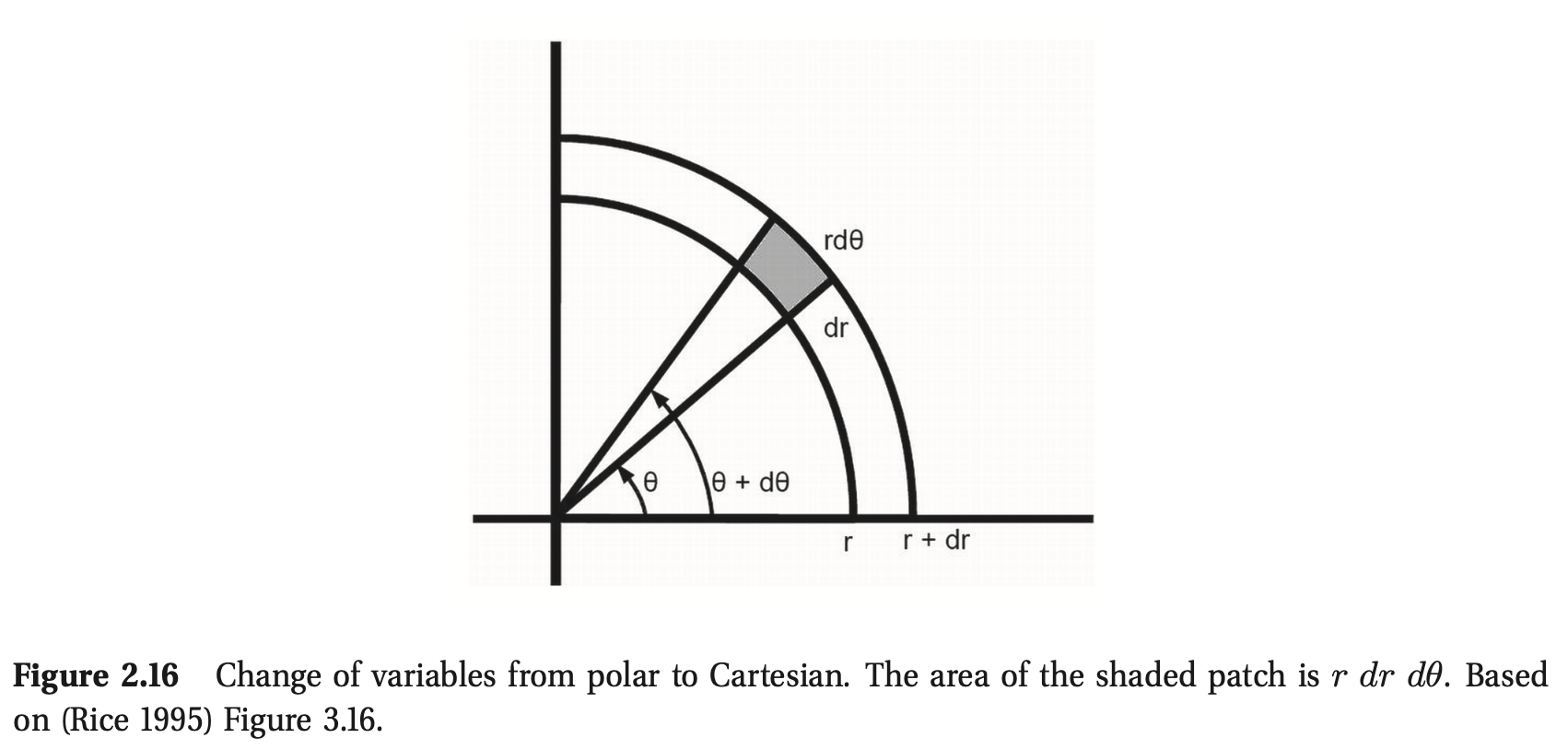
在极限情况下，这等于斑块中心的密度\(p(r,θ)\)乘以斑块的大小\(r\ dr\ dθ\)。因此

\[p_{r,\theta}(r,\theta)dr\ d\theta = p_{x_1,x_2}(x_1,x_2)r=p_{x_1,x_2}(r\cos\theta,r\sin\theta)r\ dr\ d\theta \tag{2.95} \]

2.6.3 中心极限定理

现在考虑\(N\)个具有pdf(不一定是高斯)\(p(x_i)\)的随机变量，每个随机变量的均值为\(μ\)，方差为\(σ^2\)。我们假设每个变量都是独立和同分布的independent and identically distributed，简称iid。令\(S_N=\sum_{i=1}^{N}X_i\)是随机变量的加和。这是随机边来个的一个简单但广泛使用的转换。我们可以证明，随着\(N\)的增加，这个和的分布接近：

\[p(S_N=s)=\cfrac{1}{\sqrt{2\pi N\sigma^2}}\exp \left( -\cfrac{(s-N\mu)^2}{2N\sigma^2} \right) \tag{2.96} \]

因此数量的分布：

\[Z_N \triangleq \cfrac{S_N-N\mu}{\sigma\sqrt{N}}=\cfrac{\overline{X}-\mu}{\sigma\sqrt{N}} \tag{2.97} \]

收敛于标准正态，其中\(\overline{X}=\frac{1}{N}\sum_{i=1}^Nx_i\)是样本均值。这叫做中心极限定理central limit theorem。

在图2.17中，我们给出了一个例子，在这个例子中，我们从beta分布中计算随机变量的均值。我们看到，平均值的抽样分布迅速收敛到高斯分布。

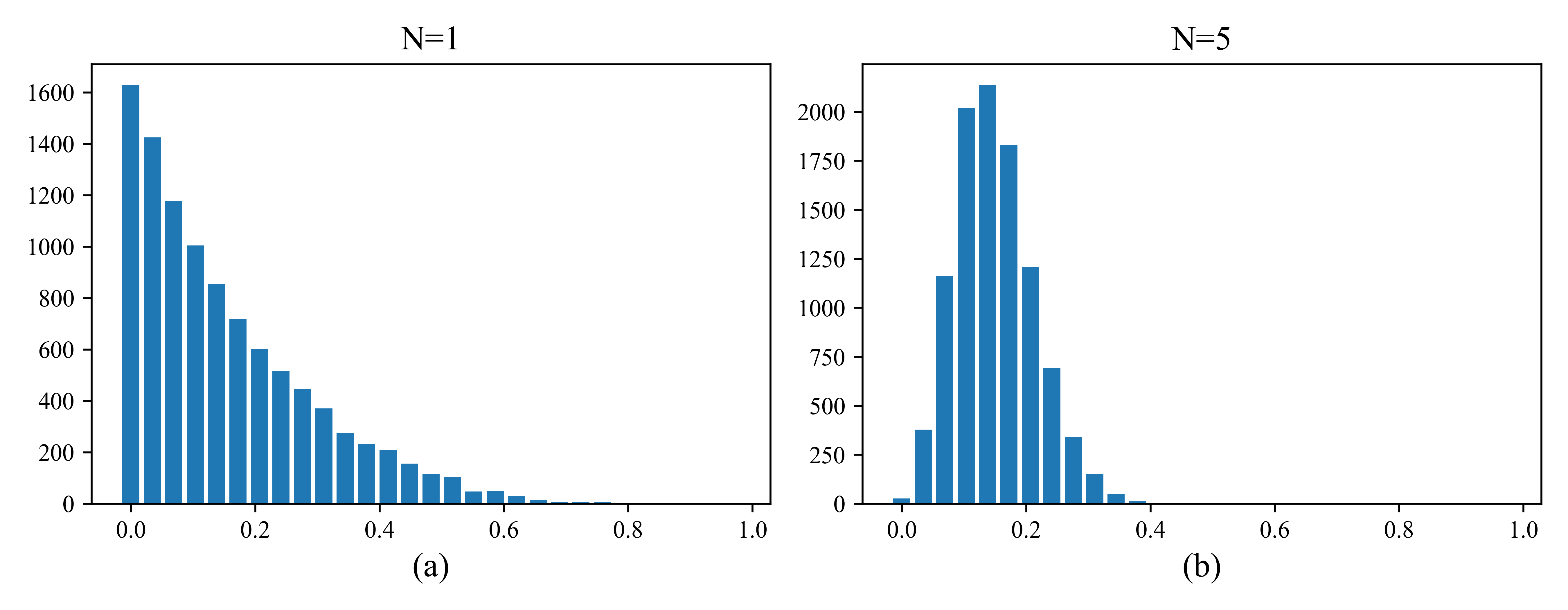
图2.17 图像中的中心极限定理。我们绘制\(\frac{1}{N}\sum^N_{i=1} x_{ij}\)的直方图，其中\(x_{ij}∼{\rm Beta}(1,5)\)，$ j = 1:10 000\(。当\)N→∞$时，分布趋于高斯分布。(a) \(N = 1\)。(b) \(N = 5\)。

2.7 蒙特卡罗近似

一般来说，用变量变换公式计算随机变量函数的分布是很困难的。一个简单但有效的替代方法如下。首先我们从分布中生成\(S\)个样本，分别记作\(x_1\ldots x_S\)。(有很多方法可以生成这样的样本；对于高维分布，一种流行的方法被称为马尔可夫链蒙特卡罗Markov chain Monte Carlo或MCMC；这将在第24章解释)。给定样本，我们可以用\(\{f(x_s)\}^S_{s=1}\)的经验分布来近似\(f(X)\)的分布。这被称为蒙特卡罗近似Monte Carlo approximate，以欧洲一座以豪华赌场而闻名的城市命名。蒙特卡罗技术最初是在统计物理领域发展起来的——特别是在原子弹的开发期间——但现在也广泛应用于统计学和机器学习。

我们可以用蒙特卡罗近似任意随机变量函数的期望值。我们简单地画出样本，然后计算应用于样本的函数的算术平均值。可以写成这样：

\[\mathbb{E}[f(X)] = \int f(x)p(x)dx \approx \cfrac{1}{S}\sum_{s=1}^Sf(x_s) \tag{2.98} \]

其中\(x_s \sim p(X)\)。这被称为蒙特卡罗积分，与数值积分(基于在固定的点网格上计算函数)相比，它有一个优势，即函数只在概率不可忽略的地方计算。

通过改变函数\(f()\)，我们可以近似许多感兴趣的量，例如

• \(\overline{x} = \cfrac{1}{S}\sum_{s=1}^S{x_s} \rightarrow \mathbf{E}[X]\)

• $\cfrac{1}{S}\sum_{s=1}^{{S}(x_s-\overline{x})}2 \rightarrow {\rm var}[X] $

• \(\cfrac{1}{S}\#\{x_s<c\} \rightarrow P(X \leq c)\)

• \({\rm median}\{ x_1,\ldots, x_S\} \rightarrow {\rm median}(X)\)

我们在下面给出了一些例子，并将在后面的章节中看到更多的例子。

2.7.1 举例：变量变换，MC方式

在第2.6.2节中，我们讨论了如何分析计算随机变量\(y = f(x)\)的函数的分布。一个更简单的方法是使用蒙特卡罗近似。例如，假设\(x∼{\rm Unif}(−1,1)\)，\(y = x^2\)。我们可以通过从\(p(x)\)中抽取许多样本，将它们平方，然后计算得到的经验分布来近似\(p(y)\)。如图2.18所示。我们将在后面的章节中广泛使用这种技术。参见图5.2。

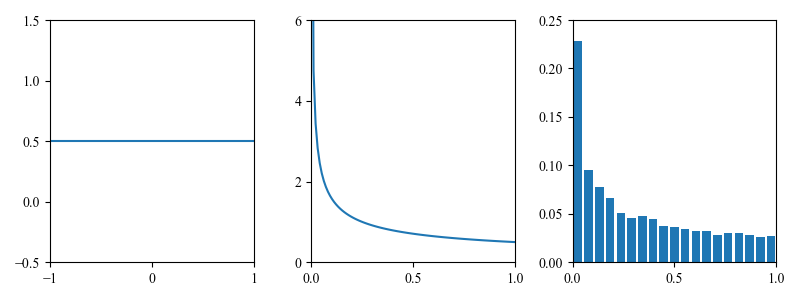
图2.18 计算\(y = x^2\)的分布，其中\(p(x)\)是均匀分布(左)。解析结果显示在中间，蒙特卡洛近似显示在右边。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

plt.rc('font',family='Times New Roman')

def func(x):
    y=x**2
    return y

_,axes = plt.subplots(1,3,figsize=(8,3))

plt.sca(axes[0])
plt.axhline(0.5)
plt.axis([-1,1,-0.5,1.5])
plt.xticks([-1,0,1])
plt.yticks([-0.5,0,0.5,1,1.5])

plt.sca(axes[1])
y1 = np.linspace(0.001,1,100)
p = 1/(2*np.sqrt(y1))
plt.plot(y1,p)
plt.axis([0,1,0,6])
plt.xticks([0,0.5,1])
plt.yticks([0,2,4,6])

plt.sca(axes[2])
data = np.random.uniform(-1,1,10000)
y2 = func(data)
bins = np.linspace(0,1,20)
weight = np.ones_like(y2)/len(y2)
plt.hist(y2,bins,weights=weight,align='mid',rwidth=0.8)
# plt.hist(y2,bins,density=True,align='mid',rwidth=0.8)
plt.axis([0,1,0,0.25])
plt.xticks([0,0.5,1])
plt.yticks([0,0.05,0.1,0.15,0.2,0.25])

plt.tight_layout()

plt.savefig('./changOfVarsdemo1d.png')
plt.show()

2.7.2 例子：用蒙特卡罗积分估计\(\boldsymbol{\pi}\)

MC近似可用于许多应用，而不仅仅是统计应用。假设我们想估算\(π\)。我们知道半径为\(r\)的圆的面积为\(πr^2\)，但它也等于如下定积分:

\[I = \int_{-r}^{r}\int_{-r}^{r}\mathbb{I}(x^2+y^2 \leq r^2)dxdy \tag{2.99} \]

因此，\(\pi=I/(r^2)\)。我们用蒙特卡罗积分来近似。设\(f(x,y) = \mathbb{I}(x^2+y^2≤r^2)\)为圆内点记为1，圆外点为0的指标函数，设\(p(x)\)和\(p(y)\)为\([−r, r]\)上的均匀分布，则\(p(x) = p(y) = 1/(2r)\)。然后

\[\begin{align} I &= (2r)(2r)\iint f(x,y)p(x)p(y)dxdy \tag{2.100}\\ &= 4r^2\int\int f(x,y)p(x)p(y)dxdy \tag{2.101} \\ & \approx 4r^2 \cfrac{1}{S}\sum_{s=1}^Sf(x_s,y_s) \tag{2.102} \\ \end{align} \]

我们发现\(\hat{π} = 3.1416\)，标准误差为0.09(关于标准误差的讨论，请参阅第2.7.3节)。我们可以将被接受/拒绝的点绘制在图2.19中。

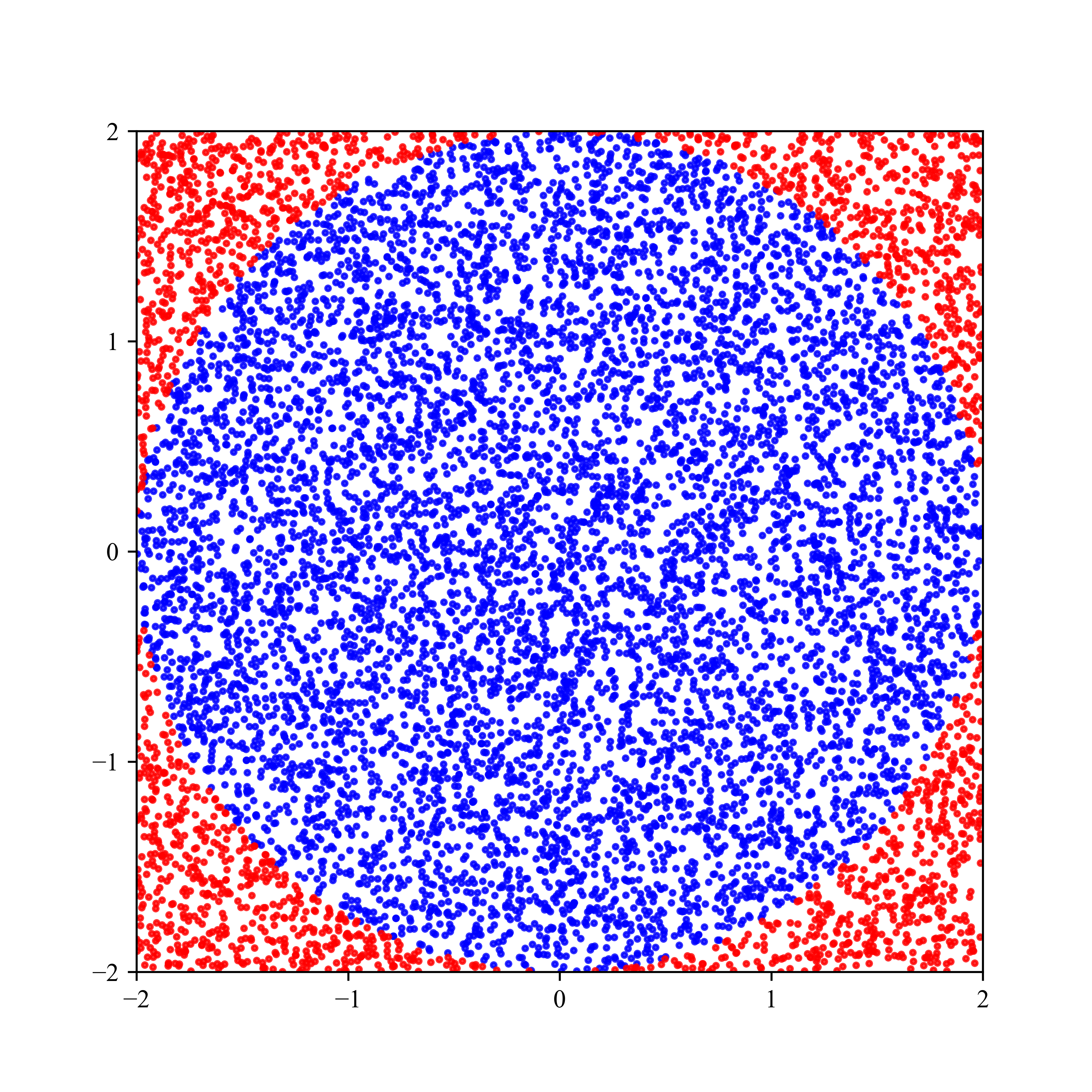
图2.19 用蒙特卡罗积分求\(π\)。蓝点在圈内，红点在圈外。

import numpy as np
import matplotlib.pyplot as plt

plt.rc('font', family='Times New Roman')

np.random.seed(42)
r= 2
x = np.random.uniform(-2,2,10000)
y = np.random.uniform(-2,2,10000)
z = (x**2+y**2<=4)*1
# 估计pi值
pi = 4*sum(z)/10000
print("估计pi值为：{}".format(pi))

plt.figure(figsize=(6,6))
plt.scatter(x[z==1],y[z==1], color='blue',s=4, alpha=0.8)
plt.scatter(x[z==0],y[z==0],color='red',s=4, alpha=0.8)
plt.axis([-2,2,-2,2])
plt.xticks([-2, -1, 0, 1, 2])
plt.yticks([-2, -1, 0, 1, 2])
plt.savefig('./mcEstimatePi.png',dpi=600)
plt.show()

2.7.3 蒙特卡罗近似的精度

MC近似的准确性随着样本量的增加而增加。如图2.20所示，在顶部一行，我们绘制了一个来自高斯分布的样本的直方图。在底线上，我们绘制了这些样本的平滑版本，使用核密度估计创建(第14.7.2节)。然后，这个平滑的分布在一个密集的点网格上进行评估并绘制。注意，这种平滑只是为了绘图，它并不用于蒙特卡罗估计本身。

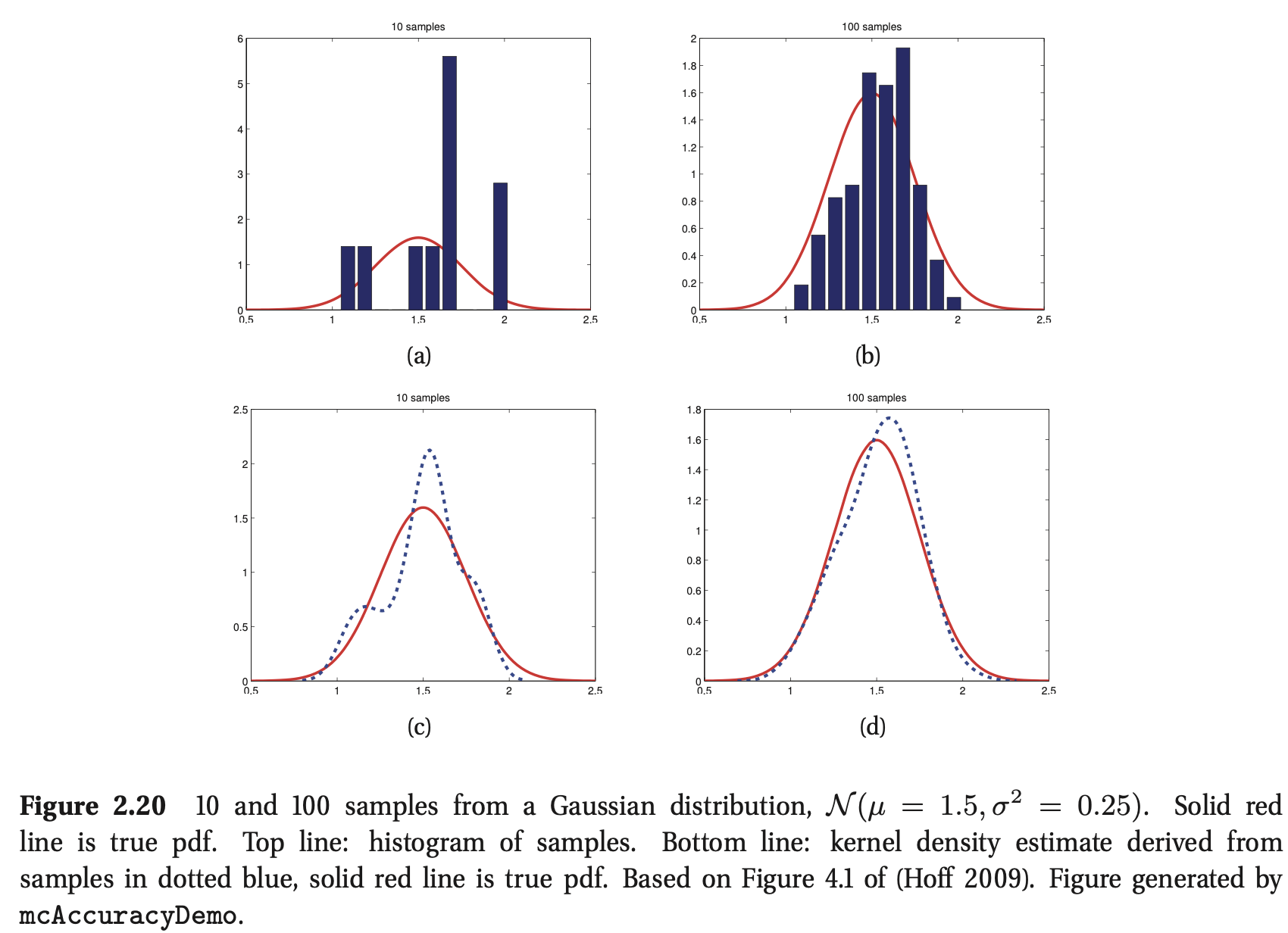
如果我们用\(μ=\mathbb{E}[f(X)]\)表示准确的平均值，用\(\hat{μ}\)表示MC近似，就可以表明，在独立样本下，

\[(\hat{\mu}-\mu) \rightarrow \mathcal{N}(0,\cfrac{\sigma^2}{S}) \tag{2.103} \]

其中：

\[\sigma^2 = {\rm var}[f(X)] = \mathbb{E}[f(X)^2]-\mathbb{E}[f(X)]^2 \tag{2.104} \]

这是中心极限定理的一个结果。当然，\(σ^2\)在上面的表达式中是未知的，但也可以用MC来估计：

\[\hat{\sigma}^2 = \cfrac{1}{S}\sum_{s=1}^{S}(f(x_s)-\hat{\mu})^2 \tag{2.105} \]

然后我们有：

\[P \left \{\mu-1.96\frac{\hat{\sigma}}{\sqrt{S}} \leq \hat{\mu} \leq \mu+1.96\cfrac{\hat{\sigma}}{\sqrt{S}} \right\} \approx 0.95 \tag{2.106} \]

术语\(\sqrt{\frac{\hat{\sigma}^2}{S}}\)被称为(数值或经验)标准误差standard error，是我们对估计\(\mu\)不确定度的估计。(关于标准误差的更多讨论见6.2节。)

如果我们想要报告一个精确到\(±\epsilon\)范围内且概率至少为95%的答案，我们需要使用一些满足\(1.96\sqrt{\hat{\sigma}^2/S}\leq \epsilon\)的样本。我们可以用2近似1.96因子，得到\(S \geq \frac{4\hat{\sigma}^2}{\epsilon^2}\)。

2.8 信息理论

信息论Information theory关注以紧凑的方式表示数据(称为数据压缩data compression或源编码source coding的任务)，以及以一种对错误具有鲁棒性的方式传输和存储数据(称为错误纠正error correction或信道编码channel coding的任务)。乍一看，这似乎与概率论和机器学习的关注点相去甚远，但实际上两者之间有着密切的联系。要看到这一点，请注意，紧凑地表示数据需要将短码字分配给可能性高的位串，并将较长的码字保留给可能性较低的位串。这与自然语言中的情况类似，常见单词(如“a”，“the”，“and”)通常比罕见单词短得多。此外，解码通过噪声信道发送的消息需要对人们倾向于发送的消息类型有一个良好的概率模型。在这两种情况下，我们都需要一个模型来预测哪些类型的数据是可能的，哪些是不可能的，这也是机器学习中的一个核心问题(关于信息论和机器学习之间联系的更多细节，请参阅(MacKay 2003))。
显然，我们不能在这里深入信息理论的细节(例如，(Cover和Thomas 2006)，如果你有兴趣了解更多)。但是，我们将在本书后面介绍一些我们需要的基本概念。

2.8.1 熵

分布为\(p\)的随机变量\(X\)的熵，用\(\mathbb{H}(X)\)表示，有时也用\(\mathbb{H}(p)\)表示，是对其不确定性的度量。特别地，对于一个有\(K\)个状态的离散变量，它定义为：

\[\mathbb{H}(X) \triangleq -\sum_{k=1}^{K}p(X=k){\rm log}_2p(X=k) \tag{2.107} \]

通常我们使用以2为底的对数，在这种情况下，单位称为位bits(二进制数字的简称)。如果我们用以\(e\)为底的对数，单位叫做nats。例如，如果\(X\in\{1,\ldots,5\}\)，直方图分布\(p =[0.25,0.25,0.2,0.15,0.15]\)，得到\(\mathbb{H} = 2.2855\)。具有最大熵的离散分布是均匀分布(参见第9.2.6节的证明)。因此，对于一个\(k\)元随机变量，当\(p(x = k)= 1/K\)时，熵最大；在这种情况下，\(\mathbb{H}(X) = \log_2K\)。相反，最小熵分布(它是零)是将所有质量放在一个状态上的函数。这样的分布没有不确定性。在图2.5(b)中，我们绘制了一个DNA序列标志，每个条形图的高度被定义为\(2−H\)，其中\(\mathbb{H}\)是该分布的熵，2是最大可能的熵。因此，高度为0的条形图对应的是均匀分布，而高度为2的条形图对应的是确定性分布。

对于二进制随机变量\(X \in \{0,1\}\)的特殊情况，我们可以写成\(p(X = 1) = θ\)和\(p(X = 0) = 1−θ\)。因此熵就变成了：

\[\begin{align} \mathbb{H}(X) & = -\left[p(X=1)\log_2p(X=1) + p(X=0)\log_2p(X=0)\right] \tag{2.108} \\ & = -\left[\theta\log_2(\theta)+(1-\theta)\log_2(1-\theta)\right] \tag{2.109} \end{align} \]

这被称为二元熵函数binary entropy function，也可以写成\(\mathbb{H}(\theta)\)。我们将其绘制在图2.21中。我们看到，最大值1出现在分布均匀时，\(θ=0.5\)。

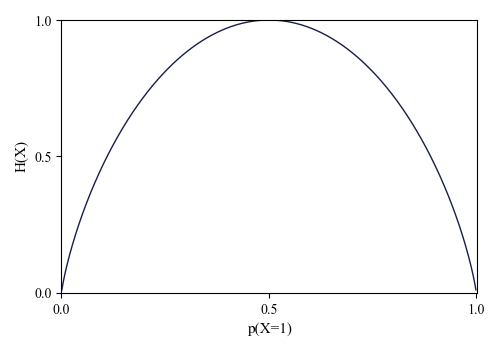
图2.21 伯努利随机变量的熵作为\(θ\)的函数。最大熵是\(\log_2 = 1\)。

import numpy as np
import matplotlib.pyplot as plt

plt.rc('font', family='Times New Roman')

def entroy(p_list):
    p_array=np.array(p_list)
    h = np.sum(-p_array*np.log2(p_array))
    return h

p_theta=np.linspace(0,1,1000)
h_list=[]
for p_list in zip(p_theta,1-p_theta):
    h_list.append(entroy(p_list))

plt.figure(figsize=(5,3.5))
plt.plot(p_theta,h_list,color='#181D4b',lw=1)
plt.axis([0,1.001,0,1.001])
plt.xticks([0,0.5,1])
plt.yticks([0,0.5,1])
plt.xlabel('p(X=1)',fontsize=11)
plt.ylabel('H(X)',fontsize=11)
plt.tight_layout()

plt.savefig('./bernoulliEntropyFig.png')
plt.show()

2.8.2 KL散度

测量两个概率分布\(p\)和\(q\)的不相似性的一种方法被称为Kullback-Leibler散度Kullback-Leibler divergence(KL散度KL divergence)或相对熵relative entropy。其定义如下：

\[\begin{align*} \mathbb{KL}(p||q) &\triangleq \sum_{k=1}^Kp_k{\rm log} \left(\cfrac{p_k}{q_k}\right) \end{align*} \tag{2.110} \]

求和被替换为pdf的积分我们可以写成：

\[\begin{align*} \mathbb{KL}(p||q) & = \sum_{k}p_k{\rm log}\left(p_k \right)- \sum_{k}p_k{\rm log}\left(q_k \right)=-\mathbb{H}(p) + \mathbb{H}(p,q) \end{align*} \tag{2.111} \]

其中\(\mathbb{H}(p,q)\)称为交叉熵cross entropy：

\[\mathbb{H}(p,q) \triangleq -\sum_kp_k{\rm log}(q_k) \tag{2.112} \]

我们可以证明(Cover和Thomas 2006)，交叉熵是当我们使用模型\(q\)来定义我们的码本codebook时，对来自分布为\(p\)的源数据进行编码所需的平均比特数。因此，第2.8.1节中定义的“规则”熵\(\mathbb{H}(p)=\mathbb{H}(p,p)\)，如果我们使用真实模型，则是期望的比特数expected number of bits，因此KL散度是两者之间的差值。换句话说，KL散度是编码数据所需的额外比特数的平均值average number of extra bits，因为我们使用分布\(q\)来编码数据，而不是真正的分布\(p\)。

“额外比特数extra number of bits”的解释应该清楚地表明，\(\mathbb{KL}(p||q)≥0\)，只有当\(q = p\)时，KL才等于零。现在我们给出了这个重要结果的证明。

定理2.8.1（信息不平等） \(\mathbb{KL}(p||q) \geq 0\)，只有\(p=q\)时 \(\mathbb{KL}(p||q)= 0\)。

证明。为了证明这个定理，我们需要使用詹森不等式Jensen's inequality。这表明，对于任何凸函数\(f\)，我们可以得到：

\[f\left( \sum_{i=1}^{n}\lambda_i\mathbf{x}_i \right) \leq \sum_{i=1}^{n}\lambda_if(\mathbf{x}_i) \tag{2.113} \]

其中，\(\lambda_i \geq 0\)，\(\sum_{i=1}^{n}\lambda_i=1\)。对于n = 2(根据凸性的定义)，这显然是正确的，对于n > 2，可以通过归纳来证明。下面让我们来证明主要定理(Cover和Thomas 2006, p28)。设\(A=\{x:p(x)>0\}\)是\(p(x)\)的支持度。然后：

\[\begin{align*} -\mathbb{KL}(p||q) &= -\sum_{x\in A}p(x) \log \left(\cfrac{p(x)}{q(x)}\right) = \sum_{x \in A}p(x) \log \left(\cfrac{q(x)}{p(x)}\right) \tag{2.114}\\ & \leq \log \sum_{x \in A}p(x)\cfrac{q(x)}{p(x)} = \log\sum_{x\in A} q(x) \tag{2.115}\\ & \leq \log\sum_{x \in \chi} q(x) = {\rm log}1 = 0 \tag{2.116} \end{align*} \]

第一个不等式是从詹森的不等式推导出来的。由于\(\log(x)\)是一个严格的凹函数，对于某些c，方程2.115 \(p(x) = cq(x)\)相等。方程2.116 \(\sum_{x \in A} q(x)=\sum_{x \in \chi} q(x)= 1\)相等，这意味着\(c = 1\)。因此，对于所有\(x\)， \(\mathbb{KL}(p||q)=0\)，当$ p(x) = q(x)$。

该结果的一个重要结论是，具有最大熵的离散分布是均匀分布。更准确地说，\(\mathbb{H}(X)≤\log|\chi|\)，其中\(|\chi|\)是\(X\)的状态数，如果\(p(X)\)是均匀的，则相等。让\(u(x) = 1/|\chi|\)。然后：

\[\begin{align} 0 &\leq \mathbb{KL}(p||u) = \sum_x p(x)\log\cfrac{p(x)}{u(x)} \tag{2.117}\\ &=\sum_xp(x)\log p(x) - \sum_xp(x)\log u(x) = -\mathbb{H}(x)+\log{\chi} \tag{2.118} \end{align} \]

这是拉普拉斯理由不充分原则Laplace's principle of insufficient reason的一个表述，它主张在没有其他理由支持一种分布而不支持另一种分布时，使用均匀分布。关于如何创建满足某些约束的发行版的讨论，请参见9.2.6节。(例如，高斯函数满足第一和第二矩约束，但在其他情况下具有最大熵。)

2.8.3 互信息

考虑两个随机变量，\(X\)和\(Y\)。假设我们想知道知道一个变量能告诉我们多少关于另一个变量的信息。我们可以计算相关系数，但这只定义为实值随机变量，而且，这是一个非常有限的依赖度量，如图2.12所示。一个更通用的方法是确定联合分布\(p(X, Y)\)与因式分布\(p(X)p(Y)\)的相似程度。这被称为互信息mutual information或MI，定义如下：

\[\mathbb{I}(X;Y) \triangleq \mathbb{KL}(p(X,Y)|| p(X)p(Y)) = \sum_x\sum_yp(x,y){\rm log}\cfrac{p(x,y)}{p(x)p(y)} \tag{2.119} \]

我们有\(\mathbb{I}(X;Y)≥0\)且只有\(p(X,Y) = p(X)p(Y)\)时相等。也就是说，如果变量是独立的，MI为零。为了深入理解MI的含义，它有助于用联合熵和条件熵来重新表示它。可以看出上述表达式等价于以下表达式：

\[\begin{align} \mathbb{I}(X;Y) &= \sum_x \sum_y p(x,y)\log \cfrac{p(x,y)}{p(x)} - \sum_x \sum_y p(x,y)\log {p(y)} \\ & =\sum_x p(x)\sum_y p(y|x)\log p(y|x) - \sum_y\log p(y) \sum_xp(x,y) \\ & = -\sum_x p(x)\mathbb{H}(Y|X=x)-\sum_y p(y)\log p(y) \\ & = \mathbb{H}(Y)-\mathbb{H}(X|Y) = \mathbb{H}(X)-\mathbb{H}(Y|X) \tag{2.120} \end{align} \]

其中\(\mathbb{H}(Y|X)\)是条件熵conditional entropy，定义为\(\mathbb{H}(Y|X)=\sum_x p(x)\mathbb{H}(Y|X=x)\)。因此，我们可以将\(X\)和\(Y\)之间的MI解释为观察\(Y\)后\(X\)不确定性的减少，或者根据对称性，观察\(X\)后\(Y\)不确定性的减少。我们将在本书后面遇到MI的几个应用。

与MI密切相关的量是逐点互信息pointwise mutual information或PMI。对于两个事件(不是随机变量)\(x\)和\(y\)，其定义为

\[{\rm PMI}(x,y) \triangleq {\rm log} \cfrac{p(x,y)}{p(x)p(y)} \tag{2.121} \]

它衡量的是这些同时发生的事件与偶然发生的事件之间的差异。显然，\(X\)和\(Y\)的\({\rm MI}\)就是\({\rm PMI}\)的期望值。有趣的是，我们可以将\(PMI\)重写如下：

\[{\rm PMI}(x,y) = {\rm log} \cfrac{p(x|y)}{p(x)} = {\rm log} \cfrac{p(y|x)}{p(y)} \tag{2.122} \]

这是我们从将先验\(p(x)\)更新为后验\(p(x|y)\)，或等价地，将先验\(p(y)\)更新为后验\(p(y|x)\)中学到的量。

2.8.3.1 连续随机变量的互信息*

上述\({\rm MI}\)公式是针对离散随机变量定义的。对于连续随机变量，通常首先将其离散化discretize或量化quantize，方法是将每个变量的范围划分为容器，并计算每个直方图容器中有多少值(Scott 1979)。然后，我们可以使用上面的公式轻松地计算\({\rm MI}\)。

不幸的是，使用的容器数量和容器边界的位置可能会对结果产生重大影响。绕过这个问题的一种方法是尝试直接估计\({\rm MI}\)，而不首先进行密度估计(Learned-Miller 2004)。另一种方法是尝试许多不同的容器大小和位置，并计算所实现的最大\({\rm MI}\)。这个统计量经过适当的标准化后，被称为最大信息系数maximal information coefficient(\({\rm MIC}\)) (Reshed et al. 2011)。更准确地说，定义：

\[m(x,y) = \cfrac{{\rm max}_{G \in \mathcal{G}(x,y)}\mathbb{I}(X(G);Y(G))}{{\rm log}\ {\rm min}(x,y)} \tag{2.123} \]

其中\(\mathcal{G}(x, y)\)是大小为\(x×y\)的\({\rm 2d}\)网格集，\(X(G)\)，\(Y(G)\)表示变量在此网格上的离散化。(使用动态规划可以有效地执行bin位置的最大化(Reshed et al. 2011)。)现在定义\({\rm MIC}\)为：

\[{\rm MIC}\triangleq \max_{x,y:xy <B}m(x,y) \tag{2.124} \]

其中\(B\)是一个依赖于我们可以使用的箱子数量的样本大小的边界，并且仍然可靠地估计分布((Reshed et al. 2011)建议\(B = N^{0.6}\))。可以表明\({\rm MIC}\)位于\([0,1]\)范围内，其中0表示变量之间没有关系，1表示任何形式的无噪声关系，而不仅仅是线性关系。
图2.22给出了该统计数据的实际示例。这些数据由世界卫生组织(世卫组织)收集的357个变量组成，用于衡量各种社会、经济、健康和政治指标。在图的左边，我们看到了所有63,566**个变量对的相关系数 correlation coefficient **(\({\rm CC}\))与\({\rm MIC}\)的关系。在图的右侧，我们看到了特定变量对的散点图，我们现在讨论：

• 标记为C的点具有低CC和低MIC。相应的散点图清楚地表明，这两个变量(死亡人数的百分比)之间没有任何关系牙医在人口中的伤害和密度)。

• 标记为D和H的点具有高CC(绝对值)和高MIC，因为它们代表了近乎线性的关系。

• 标记为E、F和G的点具有低CC但高MIC。这是因为它们对应于变量之间的非线性(有时，如在E和F的情况下，是非函数关系，即一对多)关系。

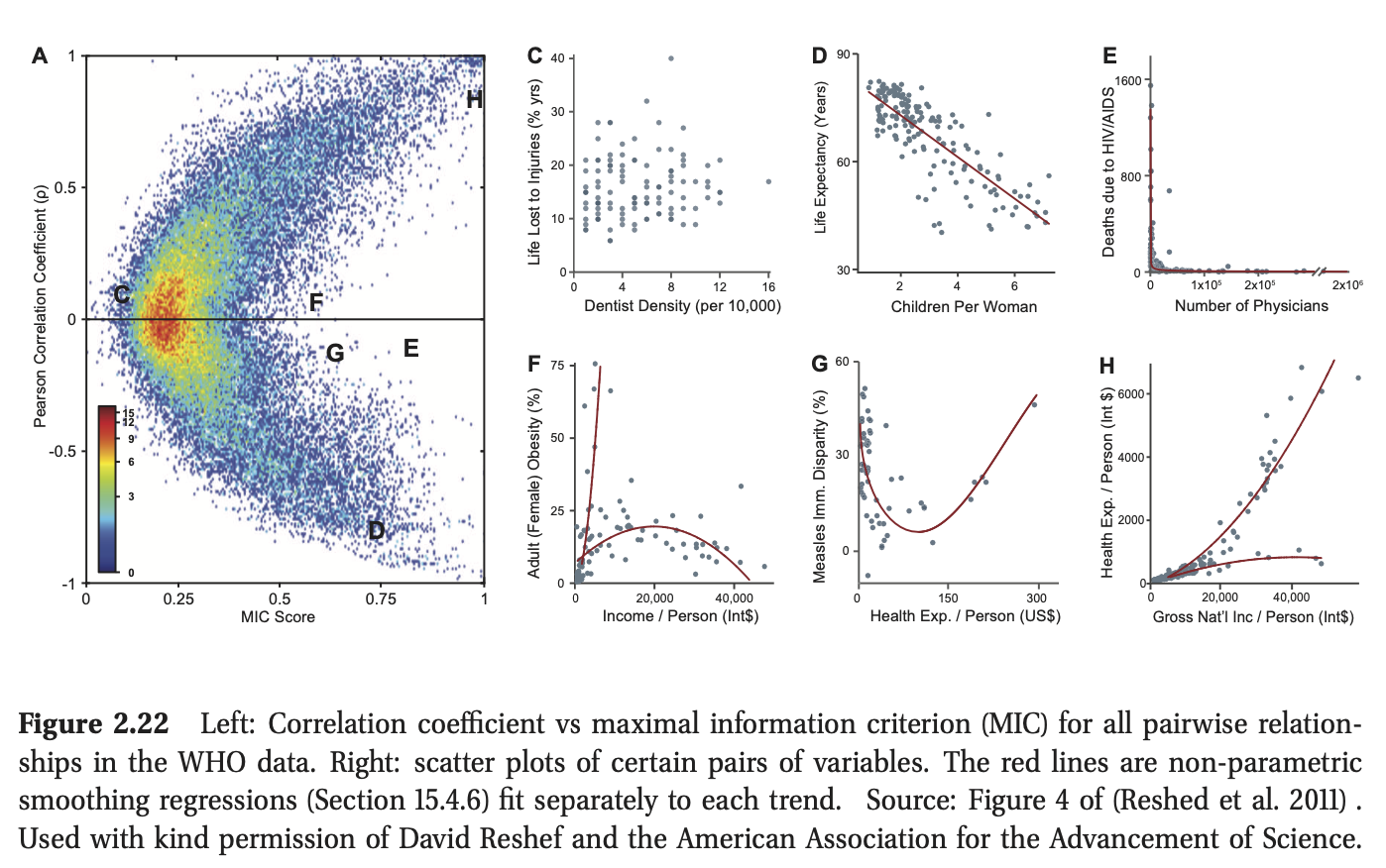
总之，我们看到基于互信息的统计数据(如MIC)可以用来发现变量之间有趣的关系，而更简单的测量方法(如相关系数)则不能。因此，MIC被称为“21世纪的相关性”(Speed 2011)。