一致性Hash算法
取模有两个主要的缺点
散列不均匀
增加节点、删除节点后节点需要rehash
为了解决上述两个主要问题,引入了一致性Hash算法。
解决散列不均匀
首先,将0到 2^32 想象成一个圆,就像钟表一样,钟表的圆可以理解成由60个点组成的圆,而此处我们把这个圆想象成由 2^32 个点组成的圆。假设有两个数据节点Node1和Node2,将它们通过一个特定的hash算法,肯定得到两个整数,恰好落在这个圆的某个点上,如图所示:

现有一批数据,通过特定的算法,也会落在这个圆上,规定数据存在顺时针最近的节点上,如图:
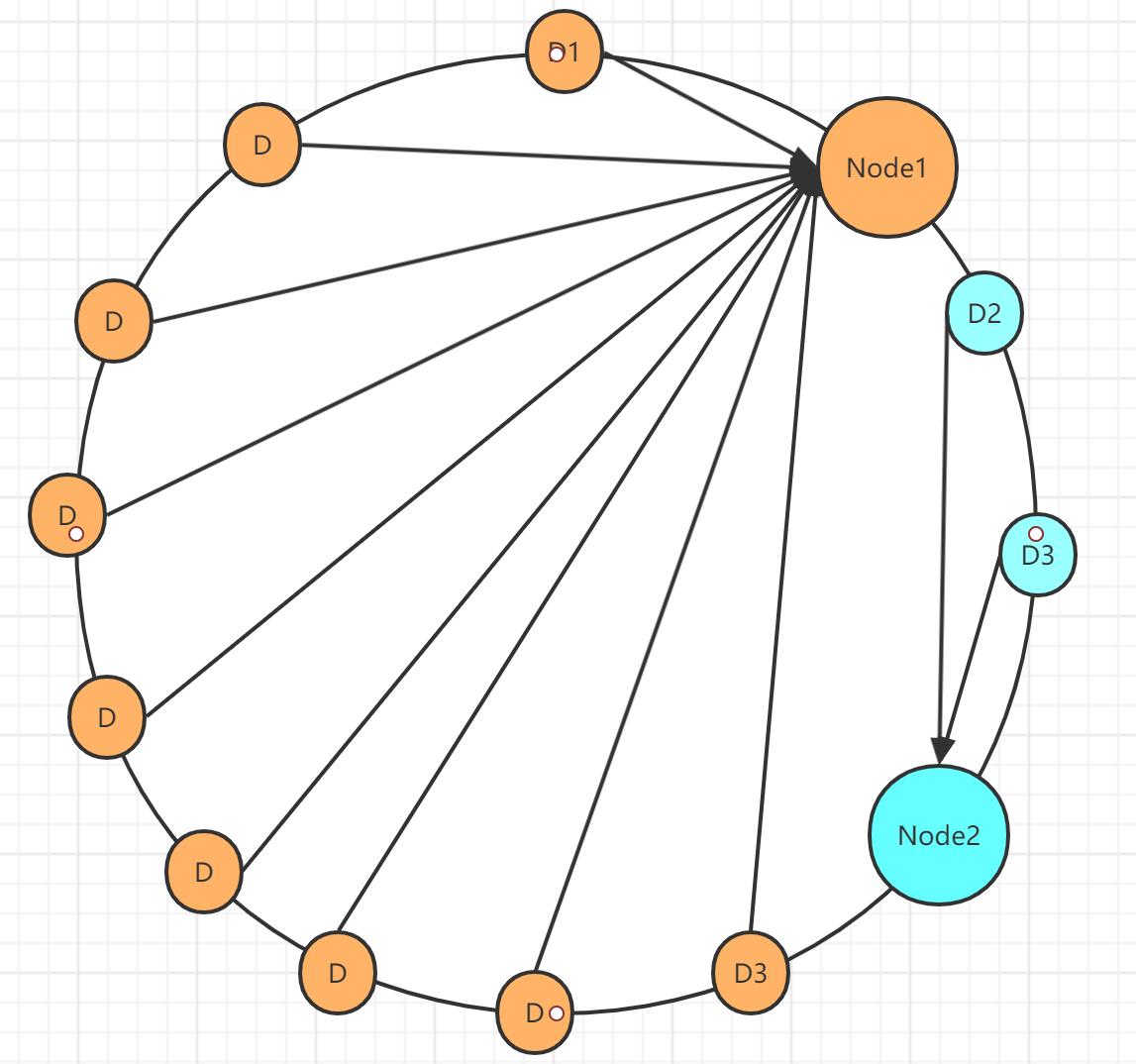
这样看起来有明显的数据倾斜问题,为了解决数据倾斜问题,则引入了虚拟节点,所谓的虚拟节点就是某个实际几点的一个映射几点,因为Node2存储的数据比较少,则虚拟出一个Node2的虚拟节点Node2-V1,将这个节点取模后的数字正好落在我们认为合适的位置,那么有些数据就会被分配到了虚拟节点上,比如下面的图:
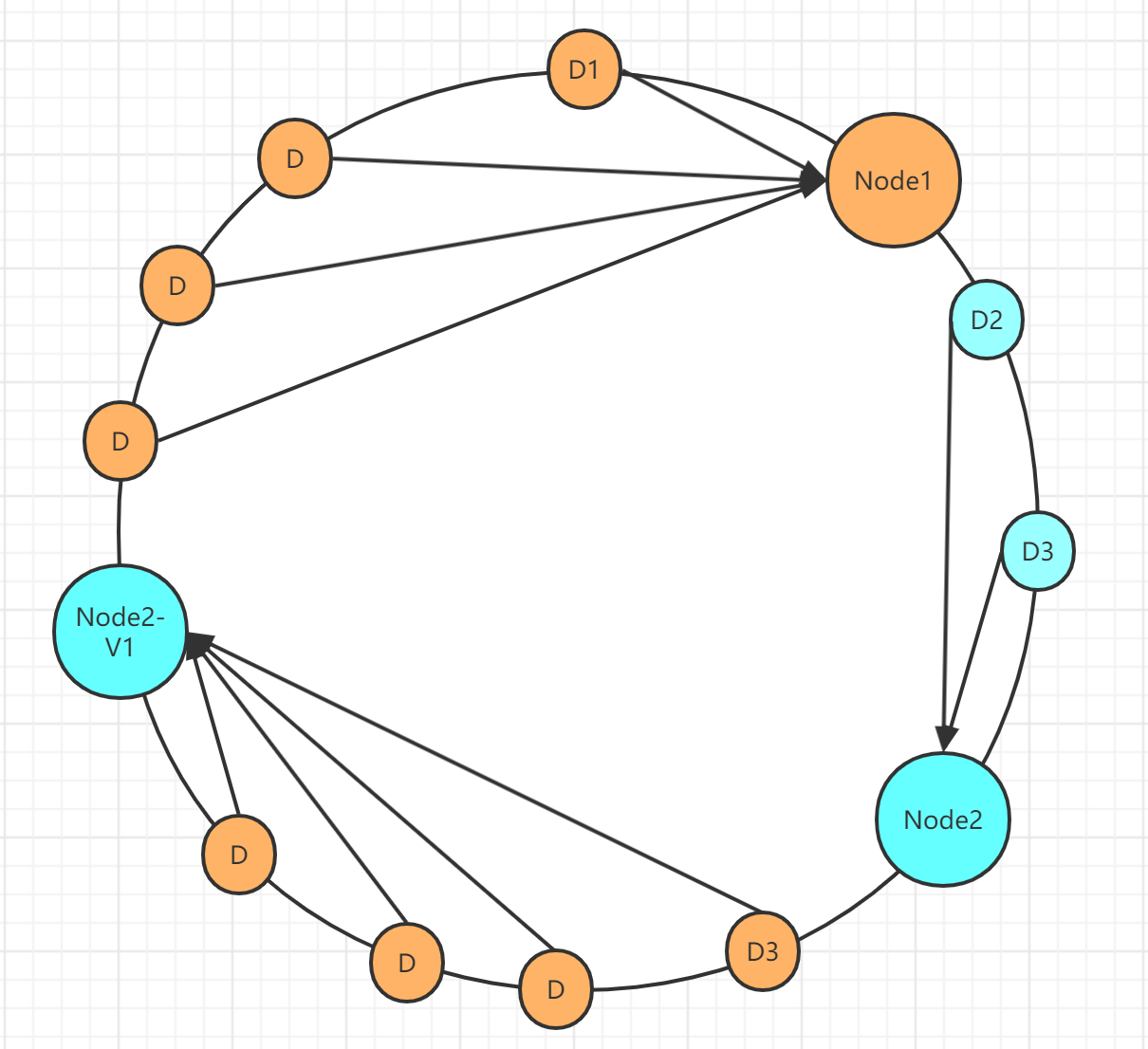
当查询或插入数据到Node2-V1节点的时候,实际上是插入到了真实节点Node2上,这样数据就被均匀的分布到了两个节点上。
解决rehash
如果按照原来取模的方式,当新增或者删除一个数据节点的时候,取模算法就有个极大的弊端,就是需要将所有数据rehash,数据迁移量比较大,如果采用一致性hash算法,极大的减少了数据迁移的量级。假设新增了一个节点Node3,数据图如下:
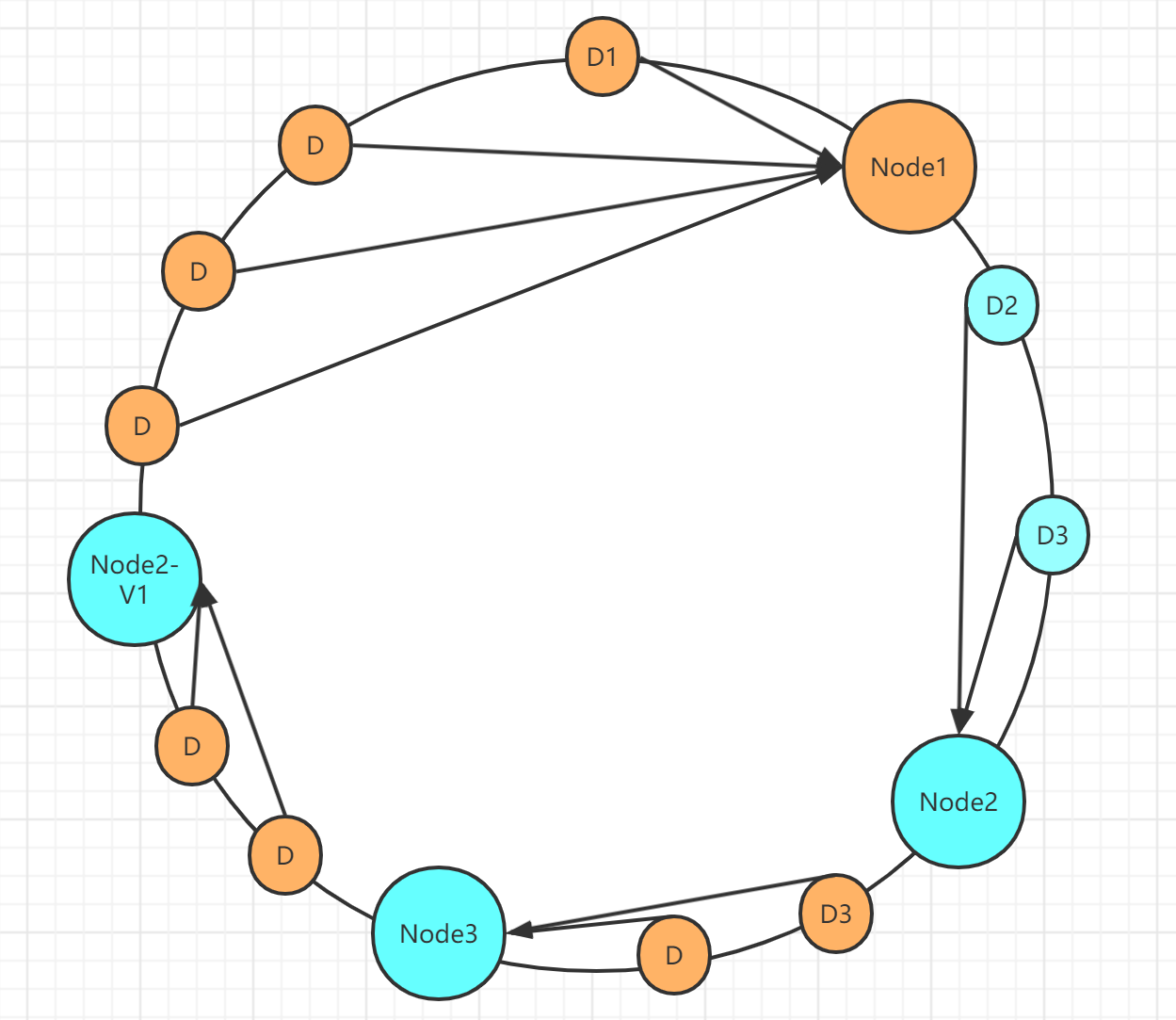
从图上可以看出,需要进行数据迁移的只有Node2和Node3中间的两个数据而已。

